Power dissipated in a fractal circuit

Electricity and Magnetism Level 5

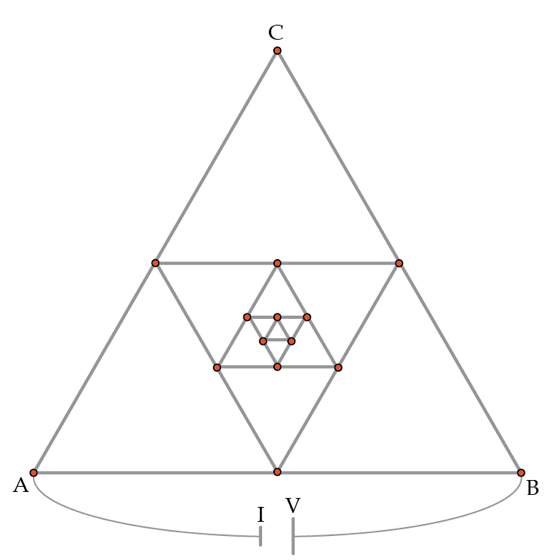
Suppose we take three homogeneous wires with resistance $R=1~\Omega$ and build an equilateral triangle ABC. Then we take more wires and we inscribe a smaller equilateral triangle inside the original one and we repeat this procedure many times to obtain a fractal circuit as shown in the figure below. What will be the total power dissipated in the circuit in Watts if a $1~\mbox{V}$ voltage source (or negligible internal resistance) is connected across points A and B?

The answer is 1.82.

2 solutions

Laplace Transform
Apr 3, 2014

the equivalent resistance is [-1+sqrt(7)]/3 so Power= [1+sqrt(7)]/2 = 1.82 watts

Well, the equivalent resistance is $\frac{446}{813}$ .

jatin yadav - 7 years, 1 month ago

Could you show your approach ? I'm getting $\rm{R}=\dfrac{ \sqrt 7 -1}{3}$ .

Vijay Raghavan - 7 years, 1 month ago

Are you assuming infinite triangles? I am assuming 5 as only 5 are shown. If you assume infinite triangles, then resistance is $\dfrac{\sqrt{7}-1}{3}$ , as it satisfies $\dfrac{1+ \frac{\frac{x}{2}}{1+\frac{x}{2}}}{2+ \frac{\frac{x}{2}}{1+\frac{x}{2}}} = x$

Infact, solving resistance for 5 triangles involves much more calculations.

jatin yadav - 7 years, 1 month ago

@Jatin Yadav – Sorry if this is really simple, but please may you explain how you got that equation jatin yadav? Thank you :)

Michael Ng - 6 years, 2 months ago

@Jatin Yadav – can you tell me how you got that equation for finding the infinite resistance of the circuit

Deepansh Jindal - 5 years, 2 months ago

Even i am getting @Vijay Raghavan 's answer.

Avineil Jain - 7 years, 1 month ago

Since the middle contact can be detached as voltage difference is 0 V as can be realized by treating differently but same resultant resistance obtainable, the combination of circuit can be simplified.

$r_0 = \frac13$ and $R_0 = \frac{1 + 2 r_0}{2 + 3 r_0}$

$r_1 = \frac12 R_0$ and $R_1 = \frac{1 + 2 r_1}{2 + 3 r_1}$

...

    r           R
   1/3         5/9  
   5/18       28/51 
  14/51       79/144
  79/288     446/813
0.274292742927429   0.548583877995643
0.274291938997821   0.548583777108899
0.274291888554449   0.548583770778653
0.274291885389326   0.548583770381455
0.274291885190727   0.548583770356532
0.274291885178266   0.548583770354968
0.274291885177484   0.548583770354870
0.274291885177435   0.548583770354864
0.274291885177432   0.548583770354864
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
(SQRT(7)-1)/6       (SQRT(7)-1)/3
14386591/52449933   28773182/52449933 {Very good proximity for infinite case.}

$\frac{446}{813}\Omega$ is the resistance for 5 triangles. Power = $\frac{813}{446} W$ = (1.822869955156950672645739910313+) W.

$Symmetry~makes~zero~difference~for~the~middles!$

Answer: $\boxed{1.8228699551569506726457399103139}$

Lu Chee Ket - 5 years, 5 months ago

Pratyush Pandey
Feb 20, 2017

I used a different approach I like to call Scaling (very useful in fractals, check out finding moment of inertia of sierpinski triangle). The trick is to realise that if the resistance across A and B is say X, then the resistance across the next inner triangle will be X/2 as for each triangle has its dimensions reduced by half compared to the immediate outer triangle and we can expect the resistance to be proportional to length. The rest is simply analysis of this circuit.

Can you explain why G is disconnected??????

Aaghaz Mahajan - 1 year, 10 months ago

Power dissipated in a fractal circuit

The answer is 1.82.

2 solutions

0 pending reports