Power of Geometry!

Triangles $\triangle OPR$ and $\triangle OSQ$ are similar since $\angle ROP=\angle SOQ$ and $\angle RSQ=\angle RPQ$ , the last two because they span the same arc of the circle.

Given similar triangles, their sizes in the ratio $4:3$ , the areas are in ratio $4^2:3^2=16:9$ .

Area of $\triangle OQS=7\cdot\frac{16}9=\boxed{12.44}$ .

By the intersecting chord theorem, $OS \cdot OR = OP \cdot OQ$ , so $4OR = 3OQ$ , or $OQ = \frac{3}{4} \cdot OR$ .

The area of $\triangle POR$ is $\frac{1}{2} \cdot OP \cdot OR \cdot \sin \angle ROP = 7$ , so $\frac{1}{2} \cdot 3 \cdot OR \cdot \sin \angle ROP = 7$ , or $OR \cdot \sin \angle ROP = \frac{14}{3}$ .

The area of $\triangle QOS$ is $A = \frac{1}{2} \cdot OS \cdot OQ \cdot \sin \angle QOS$ $=$ $\frac{1}{2} \cdot 4 \cdot OQ \cdot \sin \angle ROP$ . Substituting $OQ = \frac{3}{4}OR$ gives $A = \frac{1}{2} \cdot 4 \cdot \frac{3}{4} \cdot OR \cdot \sin \angle ROP$ , and substituting $OR \cdot \sin \angle ROP = \frac{14}{3}$ gives $A = \frac{1}{2} \cdot 4 \cdot \frac{3}{4} \cdot \frac{14}{3}$ which is equal to $A = \frac{112}{9} \approx \boxed {12.44}$ .

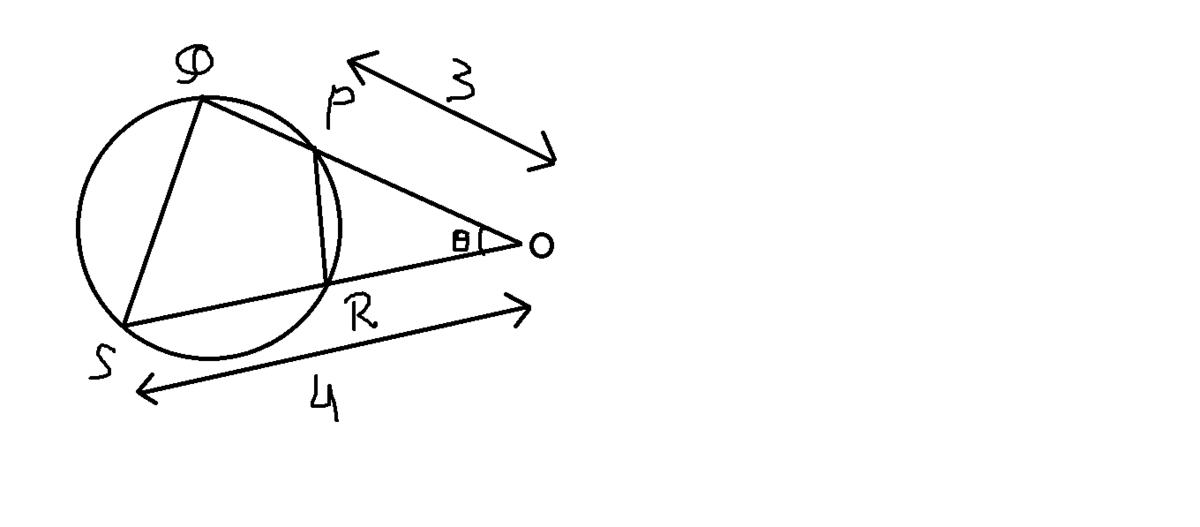
Given, $PO = 3 cm$ and $SO = 4 cm$ .

For any circle, $PO \times QO = RO \times SO$ ( Recall Power of a Circle )

Hence, $3 \times OQ = RO \times 4$ .

$\Rightarrow$ $OQ = RO \times \frac{4}{3}$ .

Area of $\triangle POR = \frac{1}{2} \times PO \times RO \times sin(\theta)$

Hence, $7 = \frac{1}{2} \times 3 \times RO \times sin(\theta)$

$\Rightarrow$ $RO \times sin(\theta) = \frac{14}{3}$

Now, Area of $\triangle QOS = \frac{1}{2} \times OQ \times OS \times sin(\theta)$

Hence, $QOS = \frac{1}{2} \times (RO \times \frac{4}{3}) \times 4 \times sin(\theta)$

$\Rightarrow$ $QOS = \frac{1}{2} \times \frac{16}{3}) \times ( RO \times sin(\theta))$

$\Rightarrow$ $QOS = \frac{8}{3} \times \frac{14}{3}$

$\Rightarrow$ $QOS = \frac{112}{9} cm^2 \approx \boxed{12.44 cm^2}$ .

Draw chord SQ.By comparing inscribed angles, triangle RPO is similar to triangle SOQ. Therefore, the ratio of areas is equal to the ratio of sides squared. So |SOQ|/7 = (4/3)^2, so area SOQ = 7*16/9 = 12..44. Ed Gray