Prime Comic Numbers

Computer Science Level 4

$\Large ...13121110987654321 \text{ is prime?}$

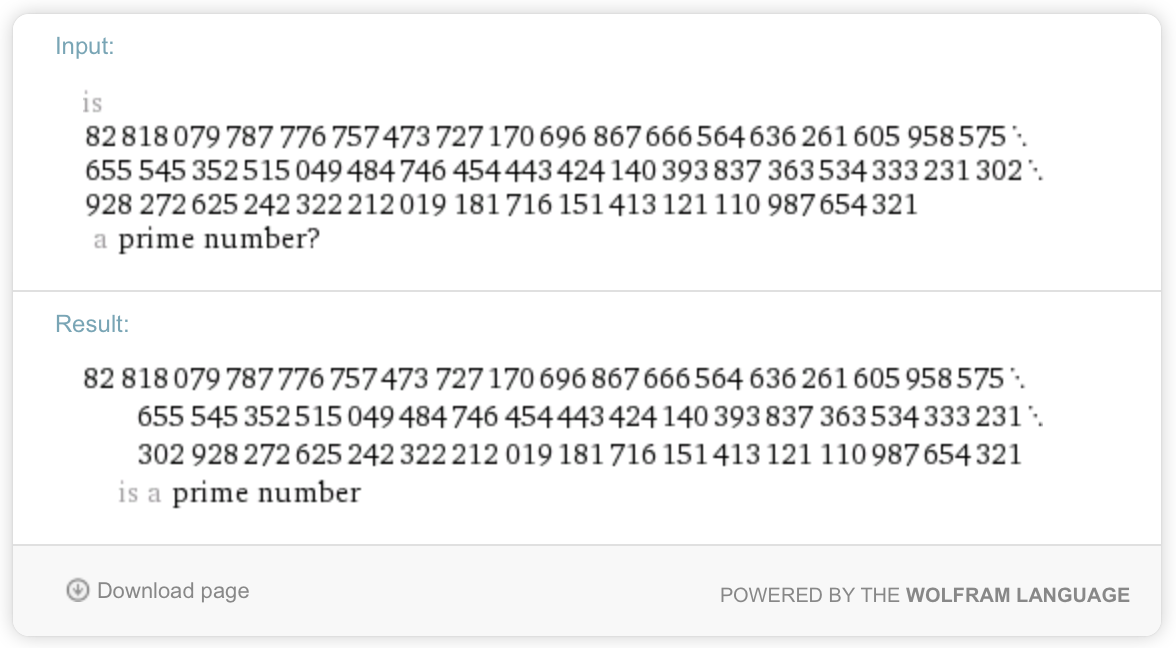
Let us define a comic number as one that is created by concatenating all of the integers from $1$ to $n$ , left to right, in descending order. For example, if we let $n=12$ , then our comic number would be $121110987654321$ . What is the first value of $n$ such that its corresponding comic number is prime?

I got the name "comic number" from the term Descending Concatenation, or D.C. for short.

The answer is 82.

5 solutions

Beakal Tiliksew
Aug 24, 2015

from gmpy2 import is_prime
i=1
while True:
  num = int(''.join(map(str,range(i,0,-1))))
  if is_prime(num):
     print (i)
     break
  i+=1

But i feel this is a bit like cheating, so here is my solution taken from ultimate with no modules.

import random

def isprime(n, precision=7):#Miller-Rabin

    if n == 1 or n % 2 == 0:
        return False 
    d = n - 1
    s = 0
    while d % 2 == 0:
        d //= 2
        s += 1
    for repeat in range(precision):
        a = random.randrange(2, n - 2)
        x = pow(a, d, n)

        if x == 1 or x == n - 1: continue

        for r in range(s - 1):
            x = pow(x, 2, n)
            if x == 1: return False
            if x == n - 1: break
        else: return False

    return True
i=1
while True:
  num = int(''.join(map(str,range(i,0,-1))))
  if isprime(num):
     print (i)
     break
  i+=1

For Miller-Rabin tests above, we know there is at most a $\frac{1}{4}$ chance for a given number and base that the "isprime" answer will be wrong. Hence we can run multiple tests with different bases and reduce the chance of error to a very substantially low level.

Garrett Clarke
Aug 23, 2015

While this is not a proof that it's the smallest, I assure you that it is prime, and that I've checked every number below it! I'd love to see some great example of computer science here; if you have a solution that allowed you to find the answer fairly quickly, please, don't be afraid to share it!

Here is something you can study : Consecutive Number Sequences

After 82, the next $n$ for which the comic number is prime is 37765, which is way hilarious :D

Satyajit Mohanty - 5 years, 9 months ago

WOW THAT IS HILARIOUS imagine if I had asked for the 2nd prime!!

Garrett Clarke - 5 years, 9 months ago

What if I make a problem : Inspired by Garrett Clarke ; and then I'll ask for the 2nd prime. :D Someone would need a super-computer to evaluate that.

Satyajit Mohanty - 5 years, 9 months ago

@Satyajit Mohanty – MY COMPUTER WOULD EXPLODE

Garrett Clarke - 5 years, 9 months ago

And then perhaps I could ask for the third such number:)! @Garrett Clarke Truly fantastic problem!

User 123 - 5 years, 9 months ago

Well if you found a 3rd number, I'm sure the mathematical community would love to hear what you have to say!

Garrett Clarke - 5 years, 9 months ago

You are a genius.

Lu Chee Ket - 5 years, 5 months ago

But why not 2 or 3 and how did u came to this conclusion.... Acc. To me if n=3 the its corresponding comic no. Is 2 and that's also a comic no. If i got the question right

Shashwat Sharan - 5 years, 9 months ago

If n=3 then its corresponding comic number is 321, which is composite.

Garrett Clarke - 5 years, 9 months ago

The only suggestions I can make is to note that all the comic numbers where "n" is a multiple of three are always composite since they also are divisible by three since the sum of the digits is divisible by three. This gives a trivial 33% improvement in a brute force search. Testing for divisibility by 11 can be done by comparing the tally of the digits of the even and odd powers of the ten, if this was done on a rolling basis then it could form a quick test.

Ed Sirett - 4 years, 8 months ago

you are right.

We can say the same for $n$ having the form $3k + 2$ for some integer $k$ . and have 66% improvement.

Abdelhamid Saadi - 4 years, 5 months ago

Abdelhamid Saadi
Aug 24, 2015

We can rapidly spot that 82 is a good candidate by the following program,

from pyprimes import isprime
def comic(n):
    return int("".join([str(i) for i in range(n,0,-1)]))

def solve():
    "Prime Comic Numbers"
    i = 1
    while(True):
        if isprime(comic(i)):
            return i
        i += 1


print(solve())

Because of the fact that $isprime$ function from $pyprimes$ is only probabilistic, we still need to verify that comic(82) is a prime number, which take a very long time.

There's nothing called probabilistic functions in C++ I guess, from what I've learnt till now and yeah I had died and born again by the time I got the answer. Why you do dis C++

Kunal Verma - 5 years, 9 months ago

Probabilistic means that a set of tests are done on number $n$ .

If one test fails the number $n$ is for sure not prime.

But if all tests pass, we are not sure that the number $n$ is prime.

Now. we are sure that $comic(n)$ for $n$ from $1$ to $81$ are not prime

And for $comic(82)$ , we have to use an other way to prove it's prime.

Abdelhamid Saadi - 5 years, 9 months ago

This actually raises the difference between science/engineering/technology and maths. If you have found that comic(82) has a less than 1/10^10 chance of actually being composite the former would say yes (why waste further time improving the score) whilst the latter can only say it is very very probable that it's a prime.

Ed Sirett - 4 years, 8 months ago

I agree with your point of view. Only it depends on the nature of application. Some cryptography algorithms need a real primes to behave as expected. if the number is not a true prime, the protection could be comprised.

Abdelhamid Saadi - 4 years, 8 months ago

Soumava Pal
Feb 19, 2016

This problem is fantastic. However this kills it. :)

Arulx Z
Jan 5, 2016

I used Miller-Rabin test -

import random
import sys

def prime(n, k = 7):
   """use Rabin-Miller algorithm to return True (n is probably prime)
or False (n is definitely composite)"""
   if n < 6:  # assuming n >= 0 in all cases... shortcut small cases here
      return [False, False, True, True, False, True][n]
   elif n & 1 == 0:  # should be faster than n % 2
      return False
   else:
      s, d = 0, n - 1
      while d & 1 == 0:
         s, d = s + 1, d >> 1
      # Use random.randint(2, n-2) for very large numbers
      for a in random.sample(xrange(2, min(n - 2, sys.maxint)), min(n - 4, k)):
         x = pow(a, d, n)
         if x != 1 and x + 1 != n:
            for r in xrange(1, s):
               x = pow(x, 2, n)
               if x == 1:
                  return False  # composite for sure
               elif x == n - 1:
                  a = 0  # so we know loop didn't continue to end
                  break  # could be strong liar, try another a
            if a:
               return False  # composite if we reached end of this loop
      return True  # probably prime if reached end of outer loop

n = '1'
count = 2

while not prime(long(n)):
    n = str(count) + n
    count += 1

print count - 1

I strongly feel that a cleverer way exists though

Moderator note:

it's unlikely that a clever approach (then testing all terms in the sequence) exists. There isn't a simply way to describe the sequence that we had. If it wasn't just concatenation, but $\sum n 10^n$ , then it is possible to look at the Arithmetic-Geometric progression sum to determine if it can be prime.

Prime Comic Numbers

I got the name "comic number" from the term Descending Concatenation, or D.C. for short.

The answer is 82.

5 solutions

Moderator note:

0 pending reports