Probability that the length of chord AB is greater than the radius of a circle.
Two points are placed randomly along the circumference of a circle. What is the probability that the chord drawn between them is longer than the radius of the circle?
How often is Length of Chord > Radius?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
16 solutions
There are multiple solutions to this problem. Ref: Bertrand paradox
Log in to reply
The reason why Bertrand found multiple solutions is based on his chord selection method. He tries these three strategies to choose a random chord:
-
Choose two random points on the circumference, and connect them to create the chord.
-
Choose a random radius on the circle, find a random point on that radius, and create the chord perpendicular to the radius which passes through the point.
-
Choose a random point within the circle, and create the chord whose midpoint is this point.
Although these all seem like valid methods to choose a random chord, they each have different chord distributions, so they will, in fact, lead to different results. The Brilliant problem resolves this interesting paradox by specifying that method 1 is being used to choose a chord.
Right! But as Zain has pointed out, Bertand's paradox does not apply here. May be you can post a problem about Bertand's paradox?
Bertrand's Paradox assumes an equilateral triangle inscribed inside the circle. The question here asks what the probability of a chord being longer than the radius of the circle is. One can draw an equilateral triangle inside a circle where the sides do not equal the radius of the circle. The two situations are separate from one another.
I agree. This is a pretty simple question. I answered 2/3 but it says I am wrong and the answer is 1/3. All the solutions provided agree at 2/3 so why is the answer shown as 1/3?
Log in to reply
I answerd 2/3 too an it said the answer is 1/2 - wtf?
Fix the first point. The second point can land within a 120 degree range to have a chord less than R. 60 to the left. 60 to the right. 120/360 = 1/3.
Write a program to simulate it and you will confirm empirically.
I solved this in following manner- In a semicircle, there can be 3 ways of drawing a chord i.e. Either it has maximum length(diameter) or its length is less than diameter,but more than radius or its length is less than radius. So, there is only 1 case out of total 3 cases when a chord drawn by joining 2 points could be greater than radius. That means Probability = 1/3. Since, we calculated it for semicircle, by doubling it we'll get the probablity for a circle. Hence answer is 2/3.
Log in to reply
Maximum length is 2r and minimum length is 0....since all lengths are equally likely.... Why not the answer is 1/2.
Let's consider the chord's distance from center.....
Since all distances (from 0 to r) are equally likely..
Those chords with length larger than r are
at a distance ranging from 0 to cos30*.
Therfore why not the answer is cos30 ?
Relevant wiki: Properties of Equilateral Triangles
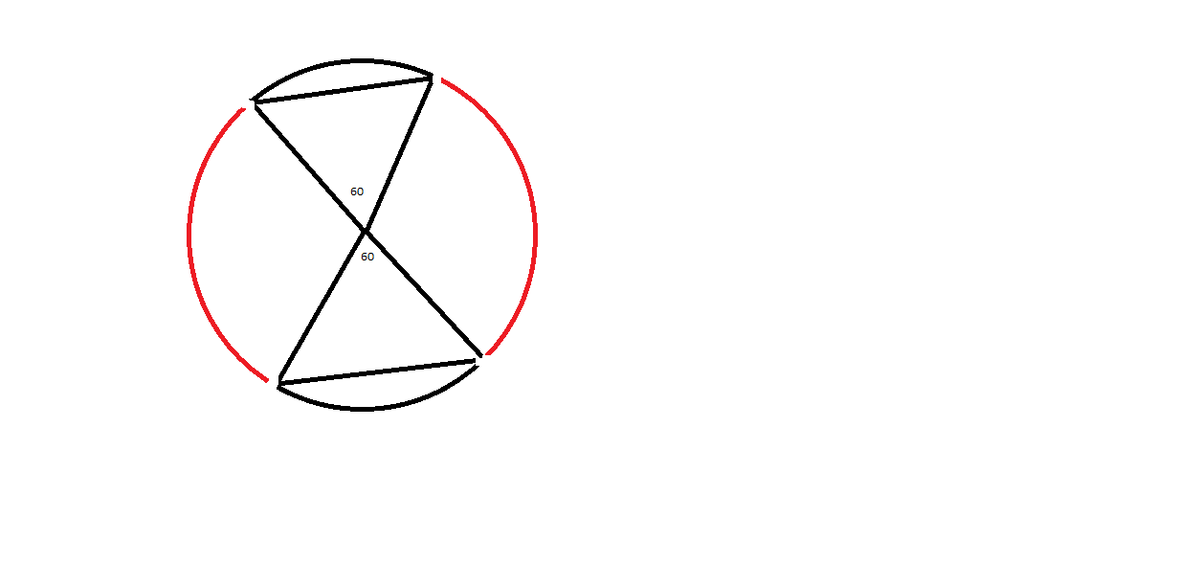
The red portion on the circumference is representative of where the points A and B can be placed for the chord to be greater than the radius of the circle.
Nice illustration!
None of the answers are correct. 5/6 is close to correct. The correct answer is sqrt(0,75). Consider setting the chord in the center. Length equal 2 x radius. Then move the chord up until length equal 1 x radius. At that point the chord has moved at a right angle on the radius according to Pythagorean theorem sqrt(1^2-0,5^2) equals sqrt(0,75).
Log in to reply
I cannot tell exactly what you mean when you say "the chord has moved at a right angle on the radius." Could you please be more specific?
Log in to reply
In other words keep the chord horizontally when you look at the problem.
- If you only consider placing the chord at equal spaced points along the circle, then yes the answer will be 2/3. But the question does not mention that requirement.
Log in to reply
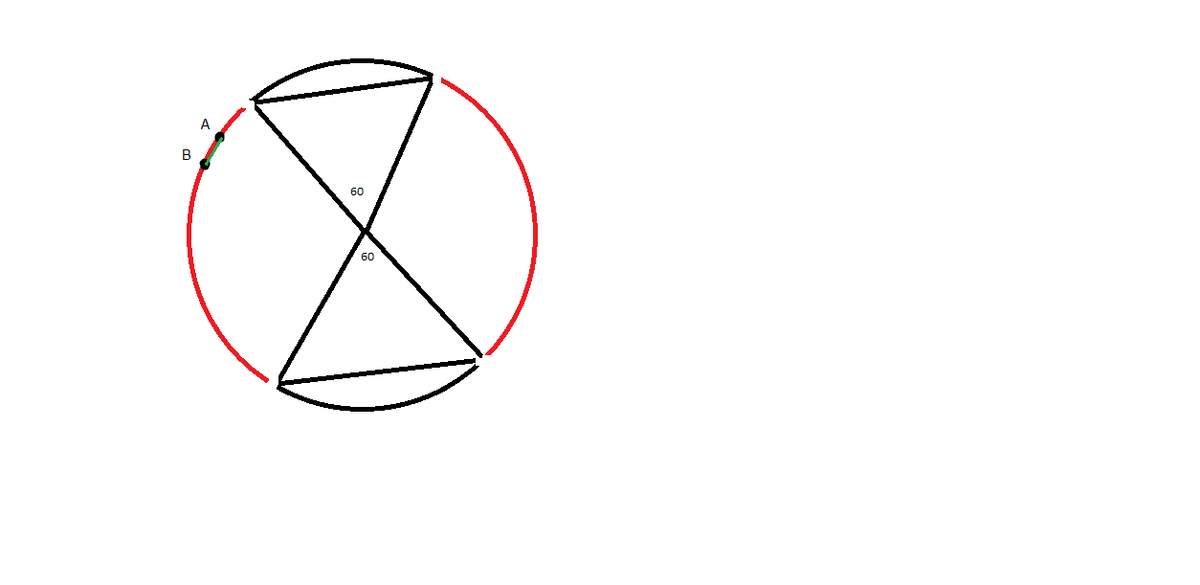
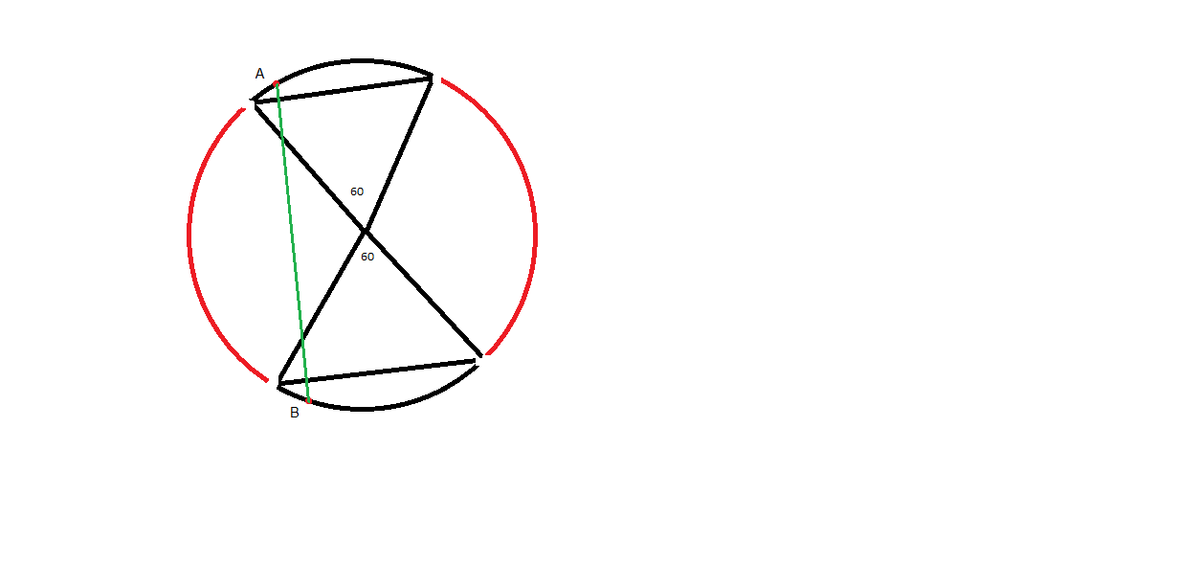
I believe I understand what you are trying to say. In the picture above, any chord perpendicular to the red line segment will be longer than the radius. The length of the red segment is 2 3 r by Pythagorean Theorem, so the probability should be 2 3 .
This is an example of the Bertrand Paradox. You can read up on it yourself, but the basic idea is that if someone uses different methods to find a random chord on a circle, it can lead to different results. According to this problem, we were supposed to choose two random points on the circle and connect them to find a random radius. You did not use this method. Instead, you chose a random radius, then chose a random point on the radius, and constructed the chord perpendicular to this point. As it turns out, using this method leads to different chords than the one stated in the problem. Here's a picture I found on Wikipedia:
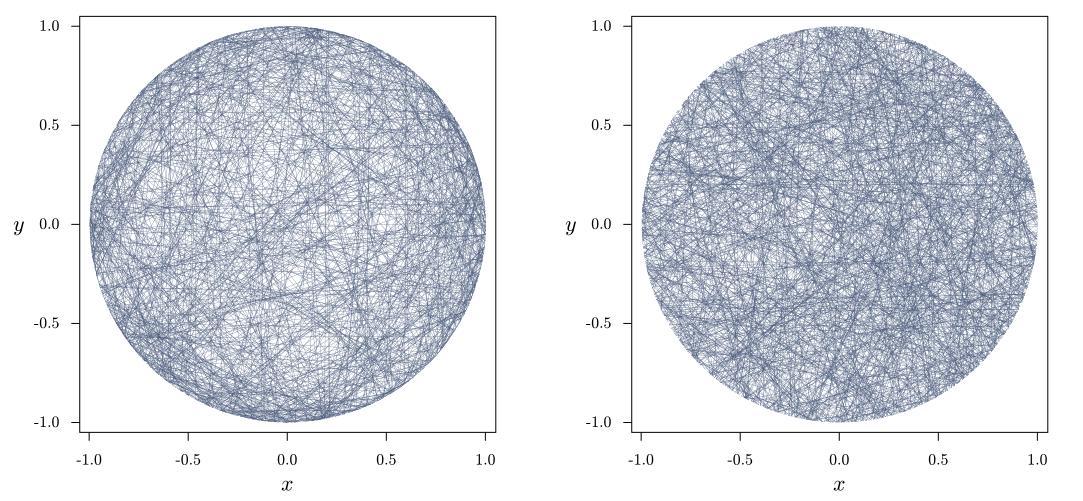
In each picture, many chords are randomly generated using a certain method. The first picture uses the method found in the problem. The second picture uses your method. It is clear that the chords generate differently, so this is why your answer is not the same as the answer to the problem.
But if the problem told us to use your method, you would be correct :)
Fix one point
Now draw a equilateral triangle having side length r vertex = centre of circle and the fixed point, chord is between the fixed point and the remaining vertex
Now rotate the chord along centre as the fixed point(towards the centre of circle) a point will come when it's length again equal to r
So the angle between them is 120
So answer is 120/180 = 0.667 APPROXIMATELY
if you think 120/180=0.667 (not 2/3), then uninstall mathematics from your brain.
Log in to reply
But 2/3 does equal 0.667 at least to 3 decimal places????
Log in to reply
That's not equality. That's the closest available representation in decimal though.
Log in to reply
@Thor - Magne Saevareid – Mathematically, that is equality, though, if it's the closest we can measurably get in terms of significant digits. 25821.5 = 25822.0 = 25822.4 if we can't see the decimal values.
You don't have to be snide about it.
Just because Yash didn't write the last line as "... 120/180 approx 0.667", that doesn't mean he/she should "uninstall mathematics from their brain" (whatever that means). It's just a small little error. You don't need to be so harsh.
Log in to reply
It's not even an error. It's just an approximation, which is perfectly valid. Sure, 2/3 is a better answer because it's 100% accurate instead of an approximation, but that doesn't mean 0.667 isn't perfectly acceptable.
Relevant wiki: Cosine Rule (Law of Cosines)
Let s , r , and θ be the length of the chord, radius, and the measure of the included angle respectively.
By law of cosine, we get
s = 2 r 2 ( 1 − c o s θ ) > r
2 r 2 ( 1 − c o s θ ) > r 2
1 − c o s θ > 2 1
c o s θ < 2 1
Notice that 0 < θ ≤ 1 8 0 and the only values that satisfy are 6 0 < θ ≤ 1 8 0 .
∴ The probablility is 1 8 0 1 2 0 = 3 2 .
The chord would equal the radius if an equilateral triangle were formed, in which case the central angle would be 60 degrees = 1/3 of the total possible of 180. therefore, a cental angle > 60 results in a chord > radius, so the answer is 2/3. Ed Gray
how do you derive 60 deg?
Log in to reply
In an equilateral triangle all angles are 60 deg
This is for people that are familiar with multiple choice questions and do a lot of them regularly. Not for people who don't appreciate humor.
This is not intended to be a formal solution for anyone to take too seriously. You'll understand what I mean about this a f t e r you properly read it.
The answer choices are 3 1 , 2 1 , 3 2 , 6 5 . 2 of these answers are above half, and 1 of them is below.
When a person is creating a multiple choice question, they usually try to make it so that the correct answer is hard to guess based on comparison to the other answer choices. They can achieve this in many different ways. For example, they generally make all the answers around the same interval. And also some other ways I don't know how to put into words. (i know you probably think i'm stupid now but continue reading anyway. please.
Going back to the beginning, more answers are concentrated above 1/2, so you can assume that the answer is probably above 1/2. *idk how to explain this, i never really tried to explain it before until now, so bear with me and my cheesy explanations. The answer probably won't be exactly 1/2 because half is such a perfect number and it's too good to be true.
eg. if the correct answer of a random question is 3/4. The creator of the question will know the general thinking process of a person trying to solve it. They will probably list the other answer choices at around the same interval. (they won't make the choices of eg 1/4, 3/2, 3/4, and 384 because 384 is obviously wrong) And since it is a fractions question, they will probably list another choice with the same numerator, and another choice with the same denominator. They will also have more answer similar to 3/4, just so it's harder to estimate the answer without actually doing calculations.
There are 2 numbers with the denominator of 3. There aren't any other 2 numbers with a common denominator. So you can assume that the answer probably has a denominator of 3. They listed 1/2 because it is a common and central number, and it is an obvious choice for what to list, because a lot of people (like noobs) will automatically assume any two random events have a 50/50 chance of happening. They probably listed 5/6 because since the correct answer is above 1/2, it is more likely for someone to guess wrong 5/6, than a number like 1/4. And 6 is a multiple of 3, so it is easy(er) for someone to make a mistake and accidentally think the denominator is 6 instead of 3.
**This is me being too lazy to calculate the answer.
or maybe just too stupid to figure out how to calculate it
maybe I'm too good at psycology.
I'm not sure
**idk stands for "I don't know"
btw, in case you were wondering, i used this method of guessing to guess the answer and i actually guessed it right.
i'm proud of me now
EDIT: THIS WEBSITE DOESN'T LET ME DO DOUBLE SPACING I'M TRIGGERED
My 'method' was along the same lines - I could tell at a glance that the probability had to greater than 1/2, and 5/6 seemed excessively high, so I plumped for 2/3.
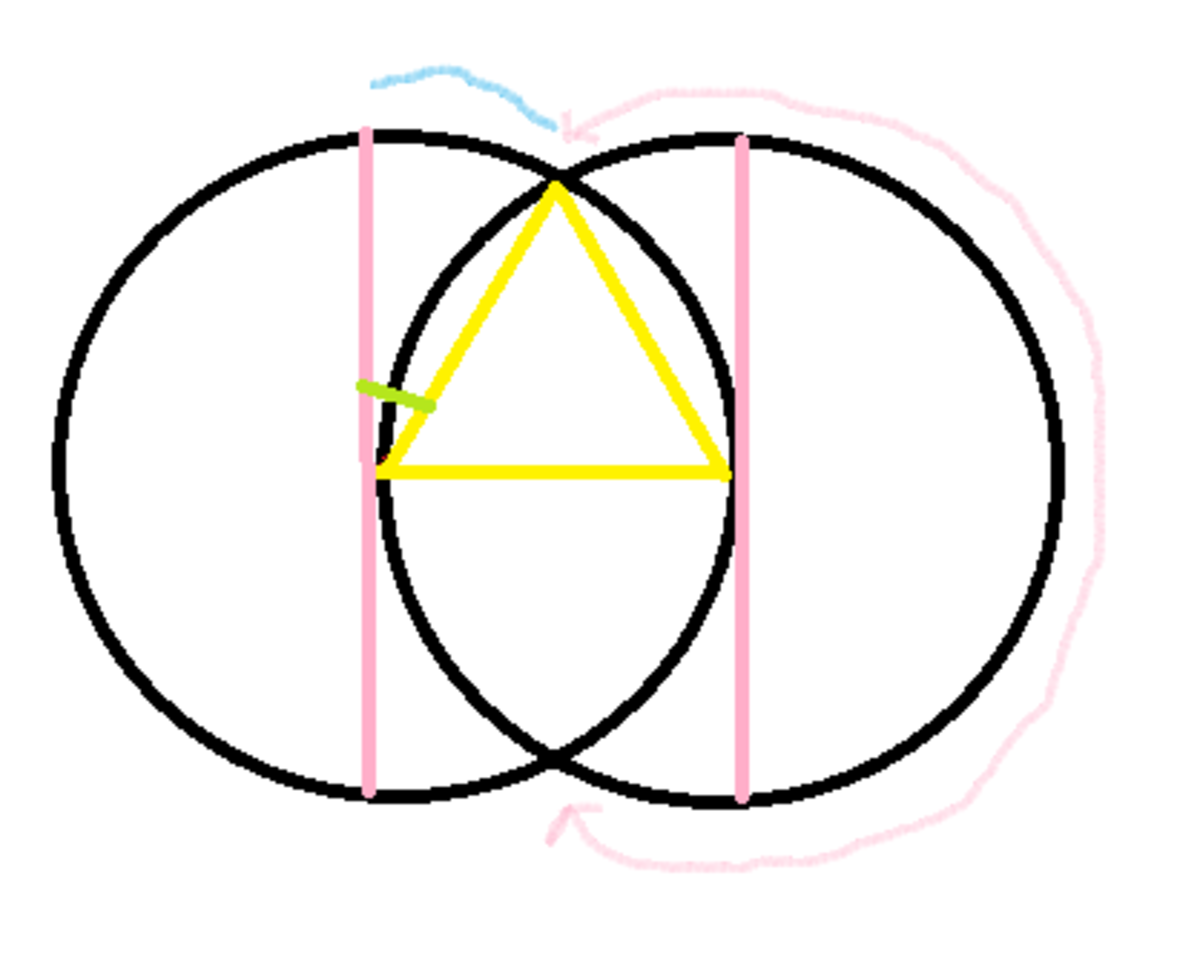
Choose any point on the circle, then draw a circle of radius r from that point as in the figure. Now any point on the pink line drawn will be at a distance > r , so we need to find out the perimeter covered by the pink line.
Pink Line = Perimeter of half circle i.e. (Pi r ) + 2 (Perimeter of the blue line).
Notice the green triangle is equilateral
Perimeter of the blue line = The blue line spans 30 degree of the circle so would be Pi r /6
Therefore Pink Line Perimeter = Pi r + 2*Pi r /6
Total circumference = 2*Pi r
Dividing them we get our answer as 2/3
What you must consider in this problem is at what point is S = R. Well, that’s when △SRR is equilateral. This is at the point where the angle between the two R sides is 60°. Given the symmetry of circles this occurs twice. Once on once half and once on the other meaning in total there are 120° of this circle where R ≤ S. This means there is 240° where S > R. Assuming the two points that the radii go to are picked completely randomly. Then given in 240° or 3 2 of the circle S is larger the probability of S being larger is when the points are random is 3 2
So yeah im stopping to think why (it's intuitive but there could possibly be something interesting...probably not) picking two points at random is equivalent probabilistically to choosing thr inner angle.
Yeah it's just the chance that the inner angle is bigger than 60 degrees (which corresponds to an aqulateral triangle which is the sorts border g event between the two outcome spaces. )
Anyway any angle bigger than sixty up to max (180) so 120 over 180....2(60)/3(60)
(pi)r = 180
r = 57(appx.)
so ratio becomes.....57 : 180
or...............................1 ; 3
so...1 - 1/3 = 2/3
Fix one point (p1) in place. Now pick a random second point(p2) on the circumference of the circle. Draw a triangle between the centre of the circle(M) , the fixed and second points. If the angle casted at M between the lines (p1M) & (p2M) is equal to 60 then the triangle formed would be an equilateral triage, thus the line (p1p2) would be exactly equal to the radius. Any lower than 60 degrees and said segment would be smaller, any larger it would be bigger. More than 180 degrees simply creates a new line, reverted from the one draw until now. So we have a case of degrees from 0 - 60 results in negative and 60-max(180) results in positive. 120/180=2/3
If we only consider half of a circle, picking randomly two points on the circle is like choosing an angle right there :
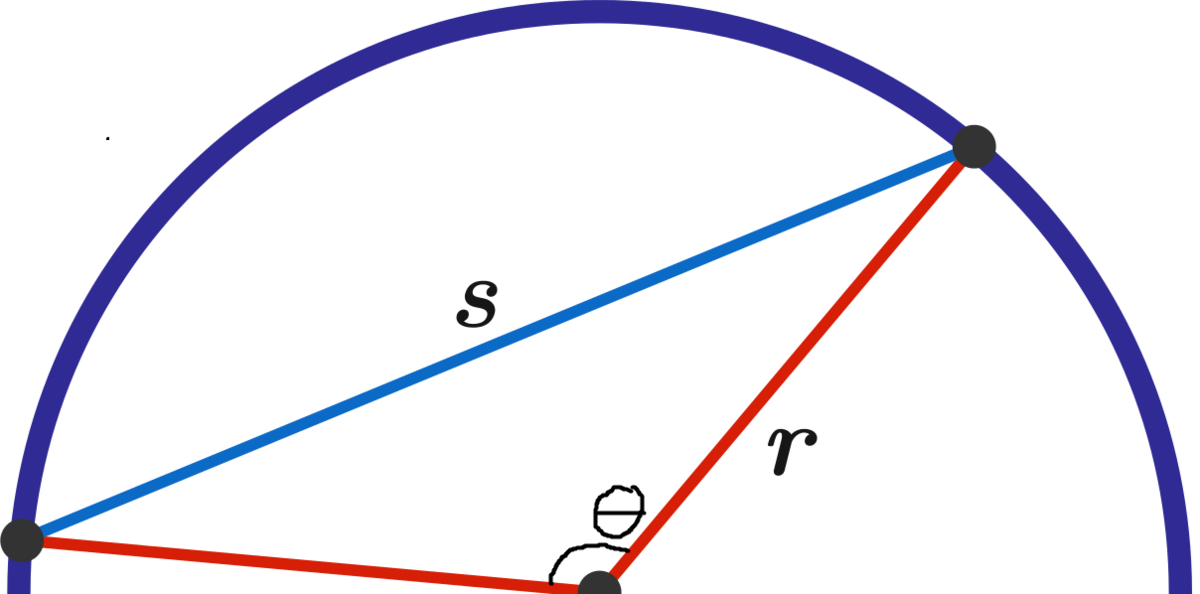
Therefore the chord is equal to the radius if the angle is 60°. If the angle is smaller than 60° then the chord will be smaller than the radius and because we can choose any angle between 0° and 180° , this situation occurs 1/3 of the time. Then we extend this solution to a full circle by adding 1/3 for the other half. Conclusion, the probabilty is 1/3 + 1/3 = 2/3
2 Solutions
1.If angle between the two radii (of the corresponding points)is greater than 60 then the above condition will be satisfied
Since the points are random the maximum angle is 180 and any angle from more than zero until 180 is possible
SO THE probability is 180-60/180 = 2/3
Second. Since the square of 3rd side if angle is ¤ is given by a^2 + b^2 - 2ab cos¤ Given that
2R^2 - 2R^2 cos¤ > R^2
Solving we get cos¤>1/2 ;i.e ¤>60
Maximum angle is 180 SO THE probability is 180-60/180 = 2/3
6 equilateral triangles, with 2 sides being radius and 1 being the chord, can fit inside of a circle (forming an hexagon shape). Remove all but 2 opposing triangles, and any isosceles triangle with a chord size bigger than the radius fits in between them, and fits the criteria.
The angle when line S is not longer than the radius starts exactly or below pi/3 rad. since there are 2 parts having pi/3 rad (opposite sides), and pi/3 rad is 1/6 of tau, that means the probability of line S being longer than the radius is 2/3 I'm 10 years old by the way..
None of these solutions are correct. However, the probability that the chord drawn between two points placed randomly along the circumference of the circle is greater than or equal to the radius of the circle is 2/3.
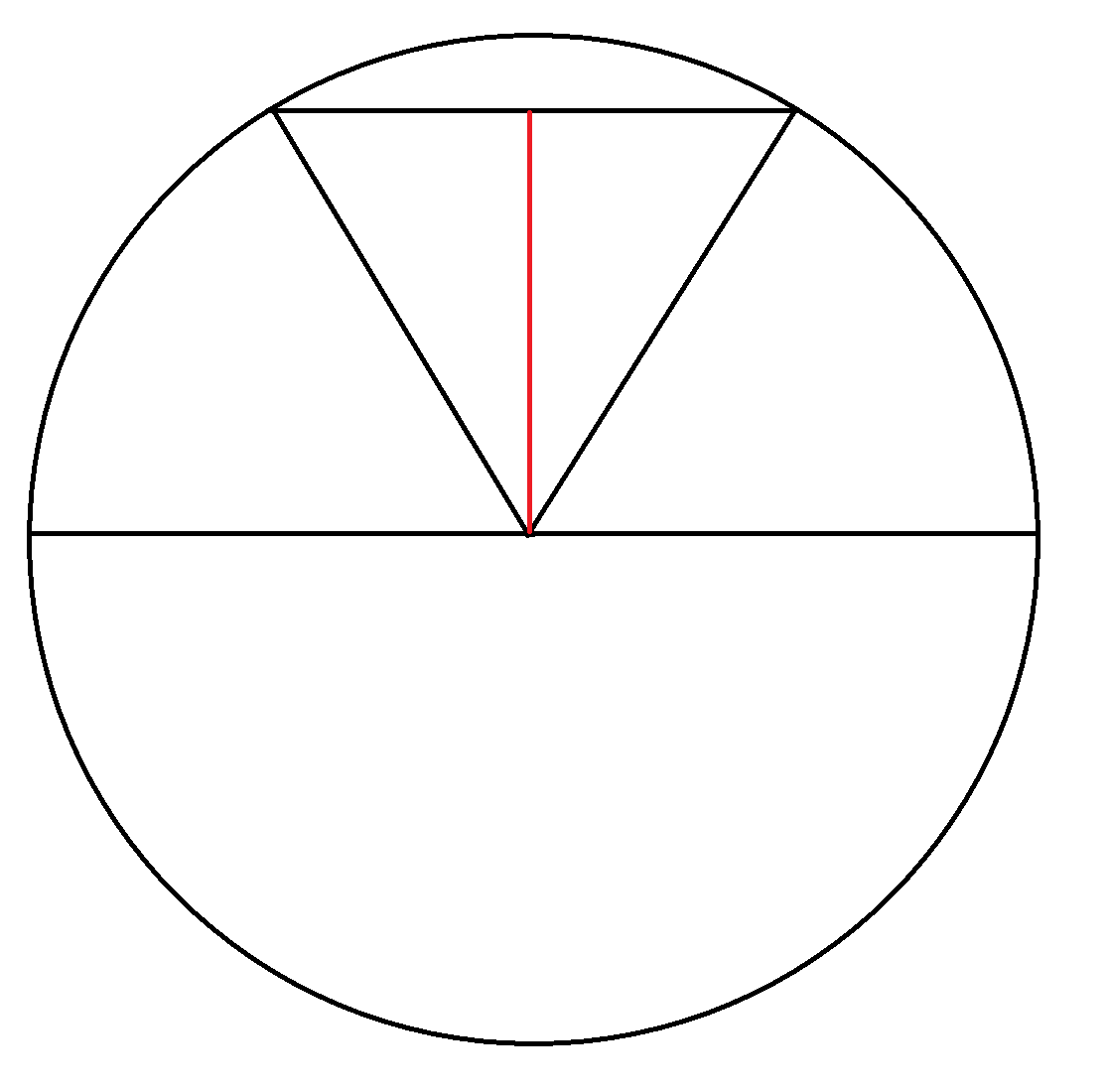
Relevant wiki: Circles Problem Solving - Basic
Consider the case where the chord is equal to the radius. Then the measure of the arc between the two points is 6 0 ∘ (it creates the equilateral triangle shown above). Now randomly select the first point. If the second point falls within 6 0 ∘ of this point, then the chord would be smaller than the radius. This is 3 6 0 ∘ 1 2 0 ∘ = 3 1 of the circumference. For the chord to be longer than the radius, the second point needs to land on the other 3 2 of the circumference.