A geometry problem by vansh gupta

Consider the diagram above. Let $r$ be the radius of the semicircle and $s$ be the side length of the square. Then by pythagorean theorem, we have

$r^2=s^2+\left(\dfrac{s}{2}\right)^2=s^2+\dfrac{1}{4}s^2=1.25s^2$ or $s^2=\dfrac{r^2}{1.25}$ (Area of the square)

The area of the semicircle is $\dfrac{1}{2}\pi r^2$ .

So the percent area occupied by the square is $\dfrac{\dfrac{r^2}{1.25}}{\dfrac{1}{2}\pi r^2}=\dfrac{1}{1.25}\times \dfrac{2}{\pi}\approx 50.9\%$

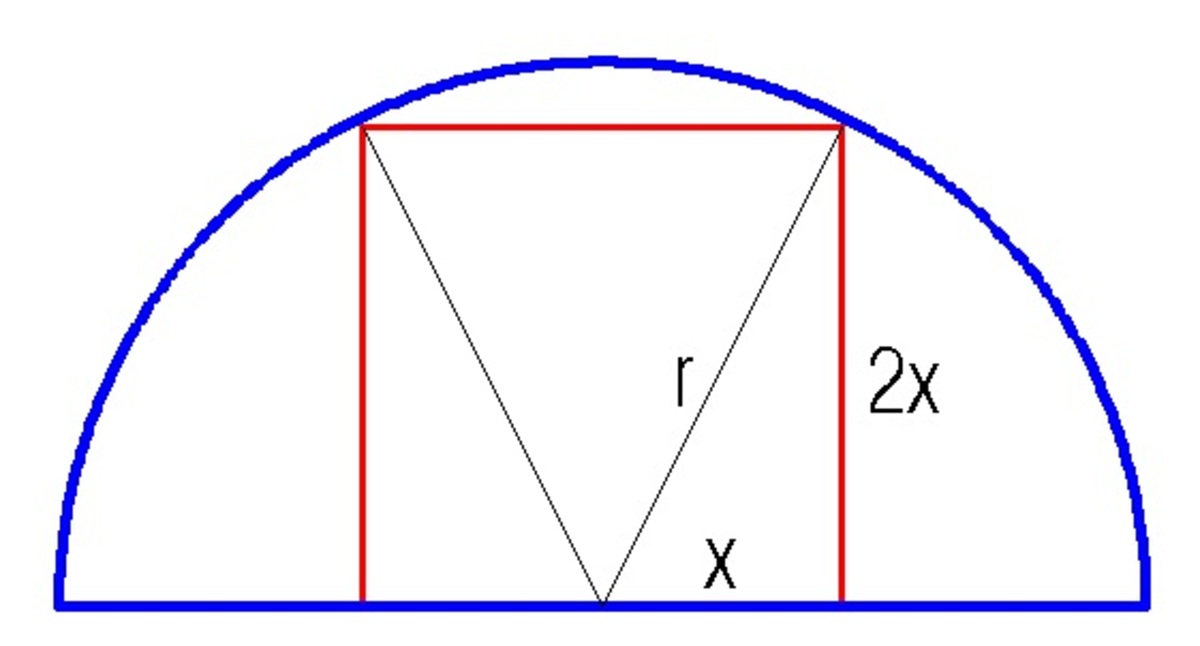By pythagorean theorem,

$r^2=x^2+(2x)^2=x^2+4x^2=5x^2$

Squaring both sides. we get

$r=x\sqrt{5}$

Solving for $x$ in terms of $r$ , we get

$x=\dfrac{r}{\sqrt{5}}$

One side of a square is therefore

$2x=\dfrac{2r}{\sqrt{5}}$

Area of the square is

$A_{square}=(2x)^2=(\dfrac{2r}{\sqrt{5}})^2=\dfrac{4}{5}r^2$

Area of the semi-circle is

$A_{semi-circle}=\dfrac{\pi}{2}r^2$

The ratio of the two areas is

$\dfrac{A_{square}}{A_{semi-circle}}=\dfrac{\dfrac{4}{5}}{\dfrac{\pi}{2}}$

It follows that,

$A_{square}=0.5093A_{semi-circle}$ (approximate)