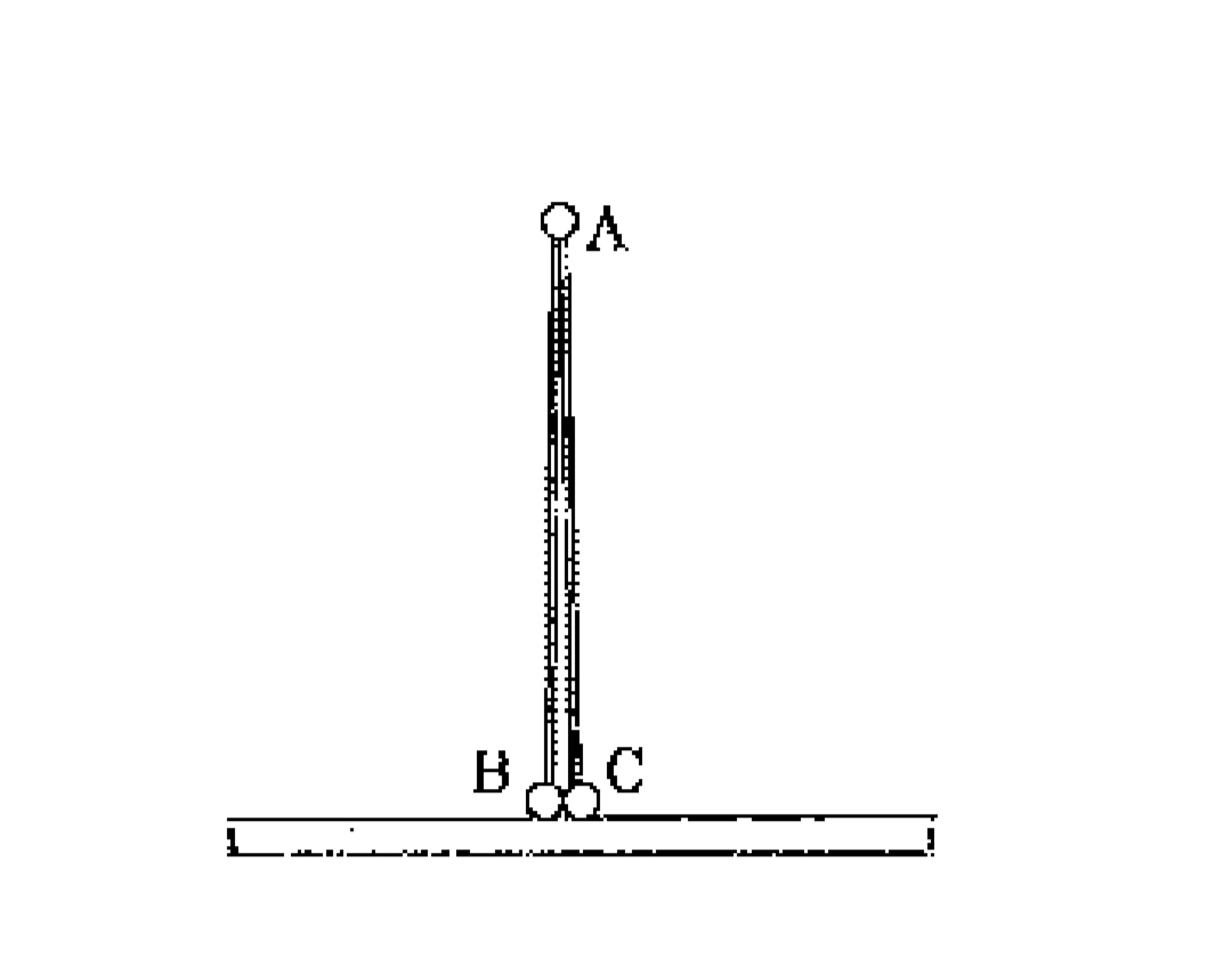
Problem in General Mechanics

Since the rods have the same length, both rods necessarily make the same angle $\theta$ with the horizontal. And we also need to define one more parameter, which is the horizontal coordinate of mass $C$ . Call this $x_C$ . The Lagrangian has three kinetic energy terms and one potential energy term.

Mass $C$ kinetic energy:

$T_C = \frac{1}{2} (2m) \dot{x}_C^2$

Mass $A$ kinetic energy and potential energy:

$x_A = x_C - \ell \cos \theta \\ y_A = \ell \sin\theta \\ \dot{x}_A = \dot{x}_C + \ell \sin \theta \dot{\theta} \\ \dot{y}_A = \ell \cos\theta \dot{\theta} \\ v_A^2 = \dot{x}_C^2 + 2 \ell \sin \theta \, \dot{x}_C \dot{\theta} + \ell^2 \dot{\theta}^2 \\ T_A = \frac{1}{2} m (\dot{x}_C^2 + 2 \ell \sin \theta \, \dot{x}_C \dot{\theta} + \ell^2 \dot{\theta}^2) \\ V_A = m g y_A = m g \ell \sin\theta$

Mass $B$ kinetic energy:

$x_B = x_C - 2 \ell \cos \theta \\ \dot{x}_B = \dot{x}_C + 2 \ell \sin \theta \dot{\theta} \\ T_B = \frac{1}{2} m (\dot{x}_C^2 + 4 \ell \sin \theta \, \dot{x}_C \dot{\theta} + 4 \ell^2 \sin^2 \theta \, \dot{\theta}^2)$

Lagrangian:

$L = T_C + T_A + T_B - V_A = \frac{1}{2} (2m) \dot{x}_C^2 + \frac{1}{2} m (\dot{x}_C^2 + 2 \ell \sin \theta \, \dot{x}_C \dot{\theta} + \ell^2 \dot{\theta}^2) + \frac{1}{2} m (\dot{x}_C^2 + 4 \ell \sin \theta \, \dot{x}_C \dot{\theta} + 4 \ell^2 \sin^2 \theta \, \dot{\theta}^2) - m g \ell \sin\theta$

Equations of motion:

$\frac{d}{dt} \frac{\partial{L}}{\partial{\dot{x}_C}} = \frac{\partial{L}}{\partial{x_C}} \\ \frac{d}{dt} \frac{\partial{L}}{\partial{\dot{\theta}}} = \frac{\partial{L}}{\partial{\theta}}$

Evaluating results in:

$\begin{bmatrix} 4 m & 3 m \ell \sin\theta \\ 3 m \ell \sin\theta & 4 m \ell^2 \sin^2 \theta + m \ell^2 \end{bmatrix} \begin{bmatrix} \ddot{x}_C \\ \ddot{\theta} \end{bmatrix} = \begin{bmatrix} -3 m \ell \cos \theta \, \dot{\theta}^2 \\ - m g \ell \cos \theta - 4 m \ell^2 \sin \theta \, \cos \theta \, \dot{\theta}^2 \end{bmatrix}$

Within a numerical integration program, solve the linear system for the double-dot terms on each time step. The speed of mass $A$ is about $1.311$ when $\theta = 60^\circ$ .

Simulation code is attached:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79

import math
import numpy as np
import random

#################################################

# Constants

deg = math.pi/180.0

dt = 10.0**(-5.0)

m = 1.0
L = 5.0
g = 10.0
theta_f = math.pi/3.0

#################################################

t = 0.0
count = 0

theta = 89.9*deg
xc = L*math.cos(theta)

thetad = 0.0
xcd = 0.0

thetadd = 0.0
xcdd = 0.0

#################################################

while theta >= theta_f:

    theta = theta + thetad*dt
    xc = xc + xcd*dt

    thetad = thetad + thetadd*dt
    xcd = xcd + xcdd*dt

    J11 = 4.0*m
    J12 = 3.0*m*L*math.sin(theta)

    J21 = 3.0*m*L*math.sin(theta)
    J22 = 4.0*m*(L**2.0)*math.sin(theta)*math.sin(theta) + m*(L**2.0)

    J =  np.array([[J11,J12],[J21,J22]])

    vec1 = -3.0*m*L*math.cos(theta)*(thetad**2.0)
    vec2 = -m*g*L*math.cos(theta) - 4.0*m*(L**2.0)*math.sin(theta)*math.cos(theta)*(thetad**2.0)

    vec = np.array([vec1,vec2])

    Sol = np.linalg.solve(J, vec)

    xcdd = Sol[0]
    thetadd = Sol[1]

    t = t + dt
    count = count + 1

#################################################

# Print results

print ""
print ""

print dt

vAsq = xcd**2.0 + 2.0*L*math.sin(theta)*xcd*thetad + (L*thetad)**2.0

vA = math.sqrt(vAsq)

print vA

#1e-05
#1.31146934239