Problem of the Day 4
x → 0 lim x + cos 2 ( x ) x − sin ( x ) = ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
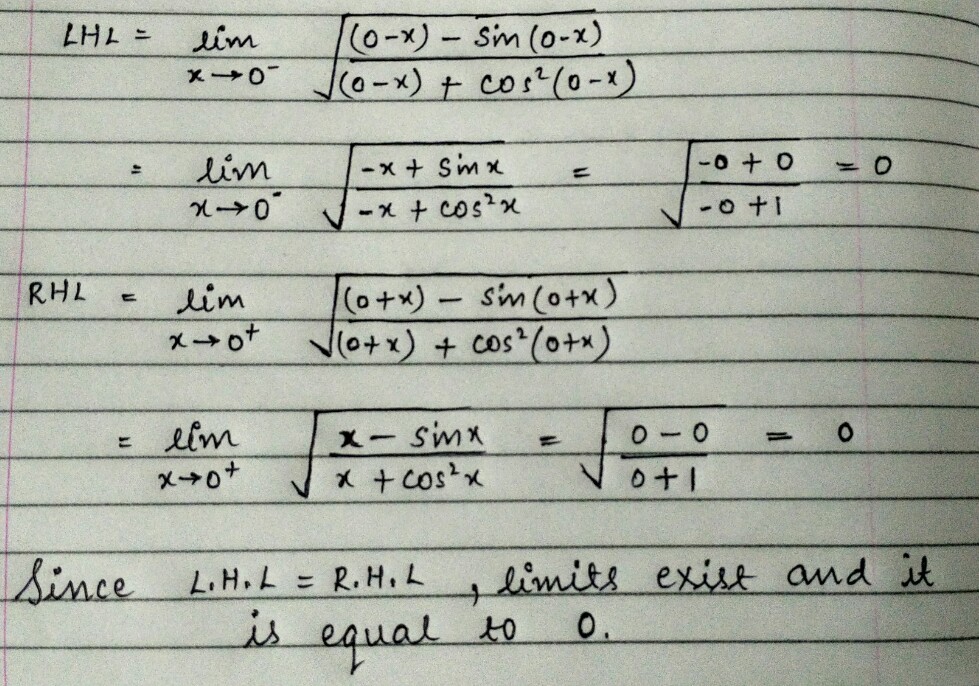
i think you should also show,LHL = RHL because that is the main aim why i added this question...
Log in to reply
Done Akhil Bansal :) :)
Log in to reply
Still incomplete solution,
You should show that . .
&
&
&
{
When
x
<
0
⇒
sin
(
x
)
>
x
,
numerator will be positive
When
x
>
0
⇒
x
>
sin
(
x
)
,
numerator will again be positive
You should numerator is positive because if it any point,numerator becomes negative,limit will not exist.(as denominator is clearly positive for both LHL and RHL)
Log in to reply
@Akhil Bansal – There's no need to do all these. You can do all the operations inside the radical first and show that it's positive at x = 0. Take its squareroot and it's still 0.
What is LHL and RHL?
Log in to reply
LHL= left hand limit and RHL = right hand limit :)