Problems With Everyday Objects: The Human Eye
 Above (constricted pupil)
Above (constricted pupil)
Below (dilated pupil)

Below (Geometric Representation
The human eye is a very beautiful and delicate part of our body.
It can show joy, sadness, boredom, and confidence with out making a sound.
When looking upon a loved one, the pupil (the black small circle in your eye) tends to dilate (increase in size). However, when we look at something that we feel indifferent to or bored of, such as the white board in history class, our pupils tend to constrict (decrease in size). Fun fact: the ratio of the width of the human head to the distance between your eyes tends to be around 1.618, or the golden ratio.
When fully dilated, the radius of the eye can be up to 4 as large as when fully constricted.
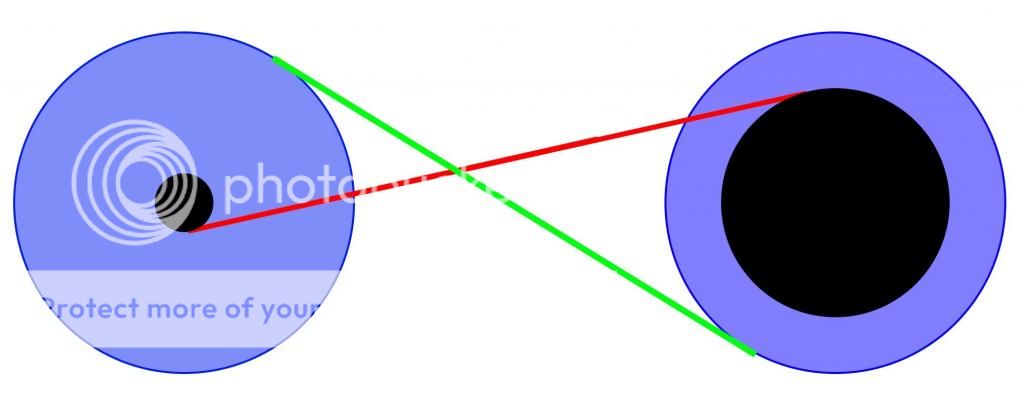
Depicted above are pictures of a constricted pupil, dilated pupil, and a geometric representation of two eyes, one constricted and one dilated.
The red and green lines are tangent to the black circles (pupils) and blue circles (irises) respectively. The left pupil is fully constricted and the right pupil is fully dilated (meaning it's radius is 4 times as large as the left one). The ratio of the radius of the constricted pupil to the radius of the entire left circle is 1:5. Finally, if the length of the red segment is 7 5 9 and the length of green segment is 1 6 1 1 , find the radius of the large black circle (dilated pupil).
(READ THIS) Trevor's Pro strats:
DO NOT TRY TO WORK WITH THE TWO NUMBERS THAT HAVE RADICALS.
Instead, begin to work with the given ratios and generalize two formulas to create a system of two equations
This problem is actually rather elegant, thus use of a computer program is not allowed, although you may use a calculator for the operations PEMDAS. Hint: the distance between the circles is integral.
All the numbers used in this problem are in millimeters. They are almost at a 1:1 scale with an actual human face.
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nice one, I didn't managed to solve the problem because I thought that the length of red line is 7 3 9 .
I apologize in advance for the sheer amount of text as there is a lot of explaining to do. I will have a geometric diagram with these lines drawn tomorrow as I left my iPad at school and thus I can't make one at the moment. Hope you like my solution!
Begin by drawing a line connecting the two circles centers, call the portion of this line that exists between the two blue circles d.
For now, label the green segment G and the red segment E .
What we are looking at here are two congruent and two similar triangles.
Working with the Green line
NOTE: all lines tangent to a circle form a 90 degree angle if a line is drawn from the point of tangency to the circle's center.
The line connecting the two circles centers will split the green line exactly in half. Infact, the point of intersection is also the midpoint between the two circles centers (aka, the mid point of d). This is because if you draw a line from both center's to their respective points of tangency, we have two right triangles with the same angles and the same bases, thus the triangles are congruent.
From this and the Pythagorean theorem, we get the equation ( b + 2 d ) 2 − b 2 = 4 G 2 where b is the radius of the large blue circle.
Working with the Red Line
The red line is much harder. Call the radius of the small black circle r and the radius of the larger black circle R.
We already know that we will have two similar triangles due to the properties of tangent lines mentioned earlier.
However, this time, one base is four times the base of the other. Thus the length of the larger triangle's longer leg is 4 times the length of the smaller triangle's longer leg. The triangle with base R 's longer leg will be of length 5 4 E because this length + 1/4 this length must equal E.
The other leg will be of length R and the hypotenuse will be 5 4 the total distance between the circles centers, or 5 4 ( b + d + b ) = 5 8 b + 4 d )
Thus by Pythagorean theorem: 2 5 1 6 E 2 = ( 5 8 b + 4 d ) ) 2 − R 2
Combining the two
So far, we have established that 2 5 1 6 E 2 = ( 5 8 b + 4 d ) 2 + R 2 and 4 G 2 = b 2 + ( b + 2 d ) 2
In the problem, we are given that 4 r = R and 5 r = B . Substituting so we are left with d and r in the two equations above.
2 5 1 6 E 2 = ( 5 4 0 r + 4 d ) ) 2 − ( 4 r ) 2 ⇒ r = 1 5 1 ( d 2 + 3 E 2 − 2 d )
4 G 2 = ( 5 r + 2 d ) 2 − ( 5 r ) 2 ⇒ r = 2 0 d G 2 − d 2
Now, we have to solve a relatively simple linear system, thus we must plug back in our original values of G and E.
1 5 1 ( d 2 + 3 ( 7 5 9 ) 2 − 2 d ) = 2 0 d ( 1 6 1 1 ) 2 − d 2
4 d 2 + 8 6 7 3 − 8 d = 8 4 4 8 − 3 d
We could bash and solve this, or we can use a little bit of logic to cut a lot of work.
Dividing both sides by four, we see the LHS is 0 ( m o d 4 ) , and since 8448 is (0 \pmod{4}) as well, d, must be divisible by four.
Now, the units digit for numbers divisible by four are 2,4,6,8, and 0. Upon squaring these digits and looking at the units digit, we get the digits 4,6, and 0.
Now, for d 2 + 8 6 7 3 to be an integer, d 2 + 8 6 7 3 must end in a 0,1,4,9,6, or 5. We see that out of the set 0,4,6, only the number 6 when added to 8673 could possibly be a perfect square.
Thus we can check d=4,16,24,36,44. After checking these, we find that only d=44 yields an integral radical. (44 mm is 2 mm less than the average distance between eyes for a human)
Plugging our value of d back into our equation gives us
r = 2 0 ( 4 4 ) ( 1 6 1 1 ) 2 − ( 4 4 ) 2 ⇒ r = 1
∴ since the ratio of r : R = 1 : 4 we have R = 4 r = 4 ( 1 ) = 4
(Another fun fact: a dilated pupil tends to be between 3-4 mm in radius)
We did it again! Apparently our brains are synchronized, (with a slight delay on my part). O.k., this is getting weird.... sigh ...... At least our approaches are different this time. :)
P.S.. I thought I was going crazy until the 2 9 4 1 got changed to 7 5 9 . Then the nice numbers popped out. Also, I had fun with your note regarding rectangles in a circle. When you get a chance, check it out. :)
Log in to reply
I wish our brains could synchronize, then my IQ would double XD. Sooo sorry about that. I accidentally did the problem assuming that the right angle occurred at the circles center's rather than the point of tangency. So that's why I ended up with 2 9 4 1 . Funny story, I only realized my error when I was typing my solution. Haha. And boom, 5 minutes later, "Brian Charlesworth has solved your problem." And at least our solutions aren't exactly the same this time. Lol
I can tell you liked that rectangle peoblem. Your solution is is genius and I've been piecing it together part by part over the past two days trying to understand it. I was thinking that for odd n it would have a symmetrical formation as well. The rest of it is pure intuition. :)
Log in to reply
Haha. When I wasn't getting an integer answer, (initially it was 4 3 5 ), I decided to look in the mirror and try and make a guess at the radius of my dilated pupil, (I was going to try 5 mm first, and if that didn't work try 4 mm). :)
Those are a nice couple of eyeballs, btw. You didn't draw either of them, by any chance? As for the rectangle problem, I'm still mulling over what to do with even n 's; packing problems are often unwieldy. This serves as an example of the potential weirdness.
Log in to reply
@Brian Charlesworth – I didn't draw any of them, I'm horrible at drawing. Lol. The best eye drawing I can do is ( • ). That's about it.
And as for even n, I believe that the rectangles' centers will spiral out, then in, then out, and in... And so forth, however, the space between the outer rectangles and the circle will eventually grow smaller than the space between the rectangles, thus at one point the pattern will become in,out,in,in,out...
Let r be the radius of the constricted pupil. Then the iris, (the blue circle), has radius 5 r and the dilated pupil radius 4 r . Also, let the distance between the centers of the two eyes be L .
Now 'shift' the red segment downward, maintaining the same slope, so that its endpoint on the right coincides with the center of the eye on the right. This endpoint has thus moved a distance 4 r , which means that, given the proportions of the eye on the left, the line segment will be tangent to this eye at P . The triangle having vertices P along with the two eye centers will then be a right triangle with legs length 5 r and 7 5 9 and hypotenuse length L .
Thus 2 5 r 2 + 2 8 9 1 = L 2 , (A).
Next, 'shift' the green segment upward, maintaining the same slope, so that its endpoint on the right coincides with the center of the eye on the right. The endpoint Q on the left will then be a distance of 1 0 r from the center of the eye on the left, such that the triangle with vertices Q and the two eye centers will be a right triangle with legs length 1 0 r and 1 6 1 1 and hypotenuse length L .
Thus 1 0 0 r 2 + 2 8 1 6 = L 2 , (B).
Equating (A) and (B) gives us that
1 0 0 r 2 − 2 5 r 2 = 2 8 9 1 − 2 8 1 6 ⟹ 7 5 r 2 = 7 5 ⟹ r = 1 ,
as we must have r > 0 . Thus the radius of the dilated pupil is 4 r = 4 .
For length of transverse common tangent(centres on opposite side) we have direct formula (Trevor's pro strats fails here :p)
Let distance between centre of 2 circles be 'd' And radius of constricted pupil 'r'
Let us solve for green line
We have
L g r e e n = d 2 − ( r 1 + r 2 ) 2
Here r 1 = r 2 = 5 r
For red
L r e d = d 2 − ( r 3 + r 4 ) 2
Here r 3 = r , r 4 = 4 r
Solving (squaring)
2 8 1 6 = d 2 − 1 0 0 r 2
2 8 9 1 = d 2 − 2 5 r 2
Eliminating 'd' we get
r = 1
4 r = 4