Projectile
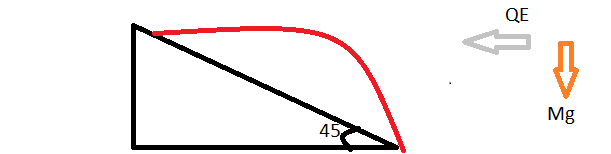 I have thrown a Ball up an inclined plane at some speed 'u' from the foot of the incline
I have thrown a Ball up an inclined plane at some speed 'u' from the foot of the incline
the incline is makes an angle of 45 degrees with the ground,
The ball carries a chage of 0.1 C and there exists a horizontal electric field of 100 N/C directed towards the incline
Find twice the maximum range on the incline
GIVEN:
1) g= 10 2)m=1 3)u= 20 all in SI units
BE CREATIVE
The answer is 56.5685.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
I truly agree with you,the concept of effective gravity is very important while dealing with mechanics problems.
Log in to reply
I believe you should remove your hint as removing it makes the problem more tough and only those who know the concept of effective gravity can do it easily.
Log in to reply
That is true. But i didnt want people to solve it in the hard way. Because if the hint enables them to think up a new way.... that would only enhance their creativity than to literally die doing the calculation and think they have actually achieved something by solving this problem. :) but yes i will remove the hint for now till some one calls it a stupid calculative problem :P
Log in to reply
@Mvs Saketh – i don't think it's difficult even i don't know Application of Effective Gravity concept. did it in an easy way than this in a shorter time.
i don't think it's difficult even i don't know Application of Effective Gravity concept. did it in an easy way than this in a shorter time.
Good Application of Effective Gravity concept...!! Really an Nice short and sweet question...!!
Yeah, same method bro +1
Find the trajectory of the projected ball and write the equation of wedges incline too , find it's intersection with the trajectory equation, and use distance formula to get the range ! Now you tell ( in comments ) who's more creative ; me ( used pure geometry) or Mvs Saketh ( used standard effective gravity approach) :)
I didn't use concept of effective gravity.
x = u t cos θ + 2 1 m q E t 2
y = u t sin θ − 2 1 g t 2
We know that y = x when ball lands on the incline.
Now we can solve for x :
x = ( m g + q E ) 2 2 m u 2 ( sin θ − cos θ ) ( m g cos θ + q E sin θ )
Fact that m g = q E comes in handy now.
x = 2 g u 2 ( ( sin θ ) 2 − ( cos θ ) 2 )
Now it's obvious that the maximum of x is when θ = 2 π
x = 2 g u 2
Range is equal to :
D = x 2 = g 2 u 2
Use forces and projectile motion to get an expression for range in terms of angle and then differentiate the term and re-substitute back into the equation.
Divide the forces qE =10 N and mg=10 N in the direction of motion of ball and in direction perpendicular of ball. qE cos 45 will support the motion of ball while mg 45 will oppose the motion and will cancel out each other.While the mg 45 and qE 45 will be perpendicular to motion pulling it down or towards the plank.Now this is equivalent to a projectile thrown on which g^' (effective gravity)= 2 q E + 2 m g .And Range= \frac{u^2 \sin 2\theta}{g^'} and we will take θ =45 to for maximum range. R= 1 0 × 2 2 0 2 ,and hence multiply it by 2 to get twice the maximum range which is the required answer..
The gravitational force is 10N and the electric force is also 10N both are directed at 90 degree to one another
the resultant is 14.14 directed at normal to incline.
hence the situation is equivalent to a projectile thrown on the ground where gravitational acceleration 'g' is equal to 14.14
so simply apply the formula
U^2/g except put g=14.14
Simple This concept of effective gravity often greatly simplifies problems :)