projectors
There's a war on the playground, and you're the charismatic leader of the Greasers. The Socs, your sworn enemies, have fashioned themselves a defensive fort, behind which they're hiding their prized possession, the crown.
The only way to win the war is by making a direct hit on the crown with a tennis ball. Blocked from a direct hit by the fort, the Greasers have to shoot it off the wall behind the fort and bank it into the crown.
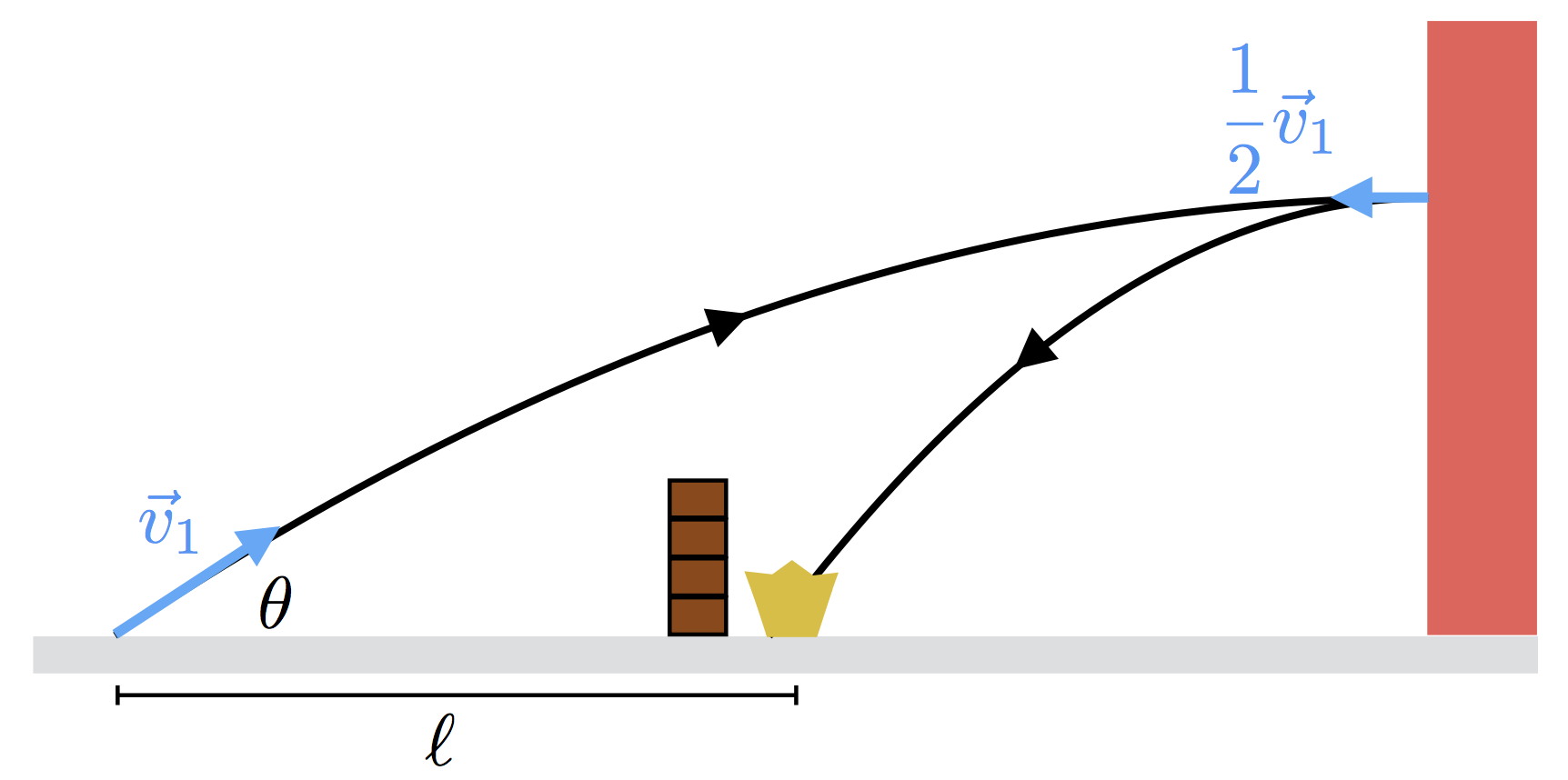
As shown in the diagram, the Greasers launch a tennis ball with speed v 1 = 2 0 m / s at an angle of θ = 6 π rad with the horizontal. At the peak of its trajectory, the ball hits the wall and reflects with speed 2 1 v 1 .
If the ball hits the crown as shown in the diagram, calculate the distance ℓ (in m ) between the launch point and the crown.
Assume that g = 9 . 8 1 m / s 2 .
The answer is 7.46229.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
The vertical velocity of the ball as it leaves the launch point is 20 x sin (pi/6), = 10m/s.
The time taken to decelerate to 0m/s vertical is 10/9.81s.
The horizontal velocity of the ball is 20 x cos (pi/6) m/s
Thus, the ball will travel horizontally 20 x cos (pi/6) x 10/9.81 m, =17.65597m.
Returning from the wall at a horizontal velocity of 10 m/s, the distance that it will travel in 10/9.81s is 10.19367m.
Then the difference between distance from launch point to the wall and wall to the crown is 7.4623m.
There is some confusion in that the velocity as the ball leaves the wall is half the initial velocity rather than half the initial horizontal velocity.
Relevant wiki: Projectile Motion
At the wall, the ball's horizontal speed changes from 1 0 3 m/s to 1 0 m/s .
Therefore instead of returning to its launch point, the ball only travels back 3 1 times as far.
The range of the projectile is g 2 v 2 sin θ cos θ ≈ 3 5 . 3 m
So l = 2 3 5 . 3 ( 1 − 3 1 ) ≈ 7 . 4 6 m .
Why the answer isn't 7 . 4 5 9 7 6 . . . . ?
Log in to reply
Because 35.3 is a rounded value:)
Log in to reply
Thanks. The last line should be l = 2 3 5 . 3 ( 1 − 3 1 ) ≈ 7 . 4 6 m .
Log in to reply
@Munem Shahriar – Good point, I've changed both lines:)
We will work with Aziz's diagram, adding d, the distance from the launch point to the wall. Notice that the time to teach the top of the trajectory and the time to fall back down from the wall to the crown will be the same. Let's call it T.
First let's apply the equation for uniform acceleration " v = a t " to the vertical component of motion, starting at the launch point and finishing at the top of the trajectory. This gives the equation
V sin θ = g T
Now let's apply the equation for unaccelerated motion " s = u t " to the horizontal component of the motion. First of all from the launch point to the wall, giving
d = V T cos θ
Then from the wall to the crown giving
d − L = 2 V T
Simple algebra with these three equations allows us to eliminate d and T to get
L = g V 2 sin θ ( cos θ − 2 1 )
Finally put in the numbers to get
L = 9 . 8 1 2 0 2 sin 6 π ( cos 6 π − 2 1 ) = 7 . 4 6 2
So, what we have and what we need.
We have:
- v 1 = 2 0 m / s
- θ = 6 π rad
- g = 9 . 8 1 m / s 2
- At the peak of its trajectory, the ball hits the wall and reflects with speed 2 1 v 1 .
We need:
- l
We can define l as l = A − B .
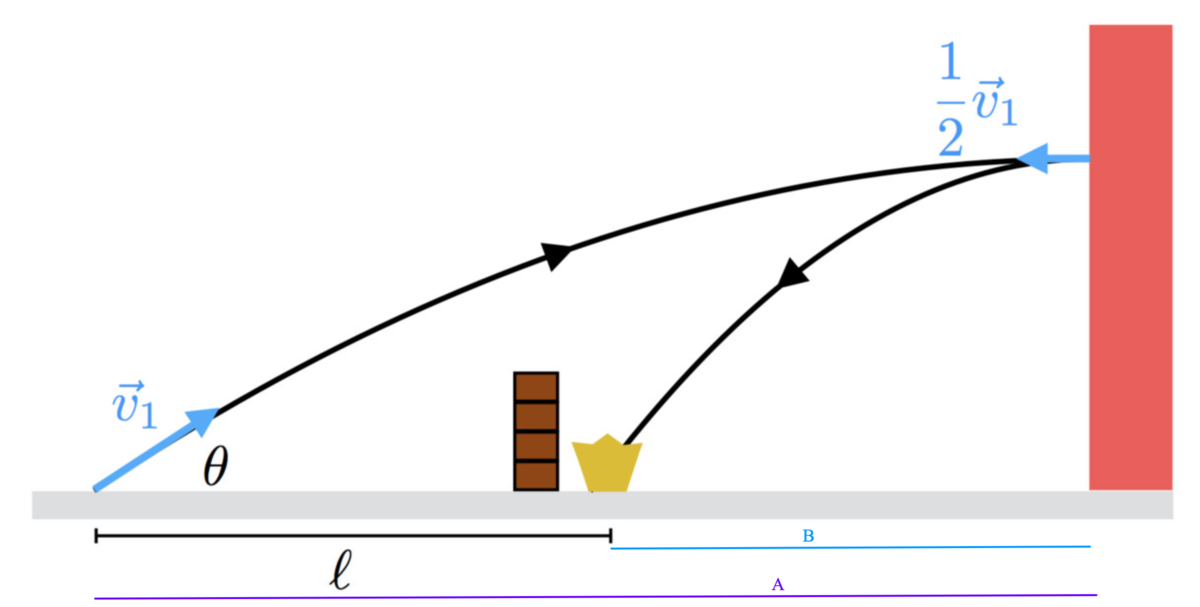
Thus we have to gather information about two distances: A and B .
Let's find A firstly. In the horizontal direction, the motion is described by the uniform velocity motion (UVM) equations of motion (acceleration in horizontal direction is 0 ):
- x ( t ) = v i x t + x i
- v x ( t ) = v i x
x i is an initial position and v i x is an initial velocity.
In the vertical direction, the motion is described by the uniformly accelerated motion (UAM) equations of motion (there is an acceleration ( g = 9 . 8 1 m / s 2 )):
- y ( t ) = 2 1 ( − 9 . 8 1 m / s 2 ) t 2 + v i y t + y i
- v y ( t ) = ( − 9 . 8 1 m / s 2 ) t + v i y
y i is an initial position and v i y is an initial velocity.
We know that the ball hit the wall at the peak of its trajectory (when the ball reaches its peak, it will have zero velocity in the y -direction), so it was when v y ( t ) = 0 .
- \(v_{ix} = v_1\cos \theta = \SI[per-mode=symbol]{20\cos (\SI{\frac{\pi}6})}{\meter\per\second} = \SI[per-mode=symbol]{10\sqrt{3}}{\meter\per\second}\)
- \(v_{iy} = v_1\sin \theta = \SI[per-mode=symbol]{20\sin (\SI{\frac{\pi}6})}{\meter\per\second} = \SI[per-mode=symbol]{10}{\meter\per\second}\)
Knowing these guys we can go further.
- v y ( t ) = ( − 9 . 8 1 m / s 2 ) t + v i y
- 0 = ( − 9 . 8 1 m / s 2 ) t + v i y
- 0 = ( − 9 . 8 1 m / s 2 ) t + 1 0 m / s
- ( − 9 . 8 1 m / s 2 ) t = − 1 0 m / s
- \(t = \SI[per-mode=symbol]{\frac{10}{\SI[per-mode=symbol]{9.81}{\meter\per\second\squared}}}{\meter\per\second}\)
- t = 1 . 0 1 9 s
Now we know we hit the wall after 1 . 0 1 9 s . So, the distance is:
- x ( 1 . 0 1 9 s ) = ( 1 0 3 m / s ) ( 1 . 0 1 9 s ) + 0 = 1 7 . 6 4 9 m
- A = 1 7 . 6 4 9 m
And the height:
- h m a x = y ( 1 . 0 1 9 s ) = 2 1 ( − 9 . 8 1 m / s 2 ) ( 1 . 0 1 9 s ) 2 + ( 1 0 m / s ) ( 1 . 0 1 9 s ) + 0
- h m a x = 5 . 0 9 6 8
Let's find B secondly. The ball hit the wall. What is going on now? The velocity has changed. Now we have:
- v 1 = 2 2 0 m / s = 1 0 m / s
When the ball hits the crown? When y ( t ) = 0 (the ball will hit the ground in this time). So, we have to calculate 0 = 2 1 ( − 9 . 8 1 ) t 2 + v i y t + y i . We need information about y i and v i y .
- \(v_{iy} = v_1\sin 0 = \SI[per-mode=symbol]{10\sin (\SI{0})}{\meter\per\second} = 0\)
- y i = h m a x = 5 . 0 9 6 8
Now, we can find a solution for this guy:
- y ( t ) = 2 1 ( − 9 . 8 1 ) t 2 + v i y t + y i
- 0 = 2 1 ( − 9 . 8 1 ) t 2 + 0 t + 5 . 0 9 6 8
- 0 = 2 1 ( − 9 . 8 1 ) t 2 + 5 . 0 9 6 8
- t = 1 . 0 1 9 3 6 s
So, we know that the ball will hit the crown after 1 . 0 1 9 3 6 s (after hitting the wall). Let's put this into x ( t ) = v i x t + x i . But, before we need to know the value of v i x .
- \(v_{ix} = v_1\cos \theta = \SI[per-mode=symbol]{10\cos (\SI{0})}{\meter\per\second} = \SI[per-mode=symbol]{10}{\meter\per\second}\)
Now we can figure out the value of x ( 1 . 0 1 9 3 6 s ) :
- B = x ( 1 . 0 1 9 3 6 s ) = ( 1 0 m / s ) ( 1 . 0 1 9 3 6 s ) + 0
- B = x ( 1 . 0 1 9 3 6 s ) = 1 0 . 1 9 3 6 m
We have A and B , so we can find out l = A − B :
- l = 1 7 . 6 4 9 m − 1 0 . 1 9 3 6 m = 7 . 4 6 m
Relevant wiki: Projectile Motion
Let the distance between the point of projection and the wall be d 1 and that between the wall and the crown be d 2 .
Now, d 1 is the distance between point of projection and the highest point in the path of projectile. So we have ( T is the time of flight of the complete projectile motion of the ball),
d 1 = v 1 cos θ ⋅ 2 T = ( v 1 cos θ ) × ( 2 1 ⋅ g 2 v 1 sin θ ) = 2 g v 1 2 sin 2 θ
The altitude of the highest point (where it hits the wall) is
h = v 1 sin θ ⋅ 2 T − 2 1 g ( 2 T ) 2 ⟹ h = v 1 sin θ ( g v 1 sin θ ) − 2 1 g ⋅ ( g v 1 sin θ ) 2 ⟹ h = 2 g v 1 2 sin 2 θ
After the projectile hits the wall (at exactly normal to the surface), the vertical velocity of the ball becomes zero and so the time it takes to come down is
h = 2 1 g t 2 ⟹ t = g 2 h = g 2 ⋅ 2 g v 1 2 sin 2 θ = g v 1 sin θ
Thus
d 2 = 2 v 1 ⋅ t = 2 g v 1 2 sin θ
The required length ℓ is expressed as
ℓ = d 1 − d 2 = 2 g v 1 2 ( sin 2 θ − sin θ ) = 2 × 9 . 8 1 2 0 2 ( sin 3 π − sin 6 π ) ≈ 7 . 4 6 2 3