Proof That 2 = 4

Calculus Level 3

What is wrong with this proof that $2 = 4$ ?

Step A:
Let ${ x }^{ {\displaystyle x }^{ {\displaystyle x }^{\displaystyle .^{.^.} } } }=y$ .
Substituting, we get ${ x }^{\displaystyle y }=y$

Step B:
$x=\sqrt [ y ]{ y }$ . Letting $y = 4$ , then $x = \sqrt[4]{4}$ and hence
${ \sqrt [ 4 ]{ 4 } }^{ {\displaystyle \sqrt [ 4 ]{ 4 } }^{ {\displaystyle \sqrt [ 4 ]{ 4 } }^{\displaystyle .^{.^.} } } }=4$

Step C:
$x=\sqrt [ y ]{ y }$ . Letting $y = 2$ , then $x = \sqrt[2]{2}$ and hence
${ \sqrt [ 2 ]{ 2 } }^{ {\displaystyle \sqrt [ 2 ]{ 2 } }^{ {\displaystyle \sqrt [ 2 ]{ 2 } }^{\displaystyle .^{.^.} } } }=2$

Step D:
Observe that $\sqrt { 2 } = 2^ \frac{1}{2} = \sqrt [ 4 ]{ 4 }$ . Hence, we get

$4 = { \sqrt [ 4 ]{ 4 } }^{ {\displaystyle \sqrt [ 4 ]{ 4 } }^{ {\displaystyle \sqrt [ 4 ]{ 4 } }^{\displaystyle .^{.^.} } } }= \sqrt [ 2 ]{ 2 } ^{ {\displaystyle \sqrt [ 2 ]{ 2 } }^{ {\displaystyle \sqrt [ 2 ]{ 2 } }^{\displaystyle .^{.^.} } } } = 2$

Which step is wrong?

Note: ${ x }^{ {\displaystyle x }^{ {\displaystyle x }^{\displaystyle .^{.^.} } } }=y$ is an infinite tetration, or infinite tower of exponentiation

A B D C

6 solutions

Brian Charlesworth
Oct 14, 2014

The maximum possible value $y$ can take in this type of equation is $e$ , corresponding to the unique solution $x = e^{\frac{1}{e}}$ . Thus the second equation in step $B$ is invalid.

For a discussion on this special value $e^{\frac{1}{e}}$ see this question .

No. $y$ can take any value in the equation $x^y=y$ as you can verify (for instance the points $(\sqrt 2,2)$ and $(\sqrt 2, 4)$ are pints that satisfy this equation. Note that $y$ is NOT a function of $x$ .

Here the question is to know for which values of $x$ the sequence $x, x^x, x^{x^x},\ldots$ converges. If it converges, then it converges to a value $y$ and satisfies $x^y=y$ but it is not true that if $x^y=y$ then the sequence converges to $y$ .

First we need to be sure that it converges for $x=\sqrt 2$ . If this is the case, it must converge to one of the values 2 or 4, but obviously not to both.

The problem is then in step B since he remark that the point $(\sqrt 2,4)$ is in the curve and implies that the sequence converges to 4, but as we see it is not a consequence form the fact that the point $(\sqrt 2, 4)$ is in the curve $x^y=y$ .

In step C he has the same problem.

Therefore, this proof is wrong in the first place because he is assuming the sequence is convergent for $x=\sqrt 2$ and second because even if he prove the sequence is convergent, he can't assume it converges to $y=2$ or to $y= 4$ just because it satisfies the equation $x^y=y$ . He must do something else to prove that it converges to one of this values.

In any case, the first mistake is step B.

To prove that the squecuence $\sqrt 2, \sqrt 2^{\sqrt 2}, \ldots$ is convergent, note that $\sqrt 2< 2$ since the function $(\sqrt 2)^x$ is increasing we have that $\sqrt2^\sqrt 2 < \sqrt 2^2 =2$ . Now by an easy induction we conclude that the sequence is bounded by 2. On the other hand, it is also easy to see that the sequence is increasing, therefore it is convergent and since it converges to either 2 or 4, but is bounded by 2, it must converge to 2.

Rogelio Pérez-Buendía - 6 years, 5 months ago

It took me a moment to make sense of the final part. So as we exponentiate it more times, since $\sqrt2^2 = 2$ the upper bound doesn't change.

In other words, what you're doing is to prove that $\sqrt2 \uparrow\uparrow n < 2$ for all $n \in \mathbb{Z}^+$ . For $n = 1$ it's obvious; for $n = k + 1$ we have $\sqrt2 \uparrow\uparrow k < 2 \\ \Rightarrow \sqrt2^{\sqrt2 \uparrow\uparrow k} < \sqrt2^2 \\ \Rightarrow \sqrt2 \uparrow\uparrow (k+1) < 2 \\$ therefore by the induction principle we can deduce that it's true for all $n$ . QED

Stewart Gordon - 5 years, 12 months ago

If step B is invalid, wouldn't that make anything that uses step B, like step D also invalid?

Hobart Pao - 6 years, 7 months ago

Nicotinamide, one can argue that Step D is wrong because it came to an obviously absurd conclusion. But the means it came to that conclusion is not. If I have a lengthy proof, a single flaw in the middle of it can potentially invalidate all the subsequent steps, but in troubleshooting a flawed proof, you need to pinpoint where it went wrong.

Michael Mendrin - 6 years, 7 months ago

I understand what you mean, but the question was vague.

Hobart Pao - 6 years, 7 months ago

@Hobart Pao – Ah, well, but I think the Brilliant staff just fixed that. Any better for you?

Michael Mendrin - 6 years, 7 months ago

Michael Mendrin
Oct 15, 2014

Here's a handy graphic that should help clear up the mystery with this one

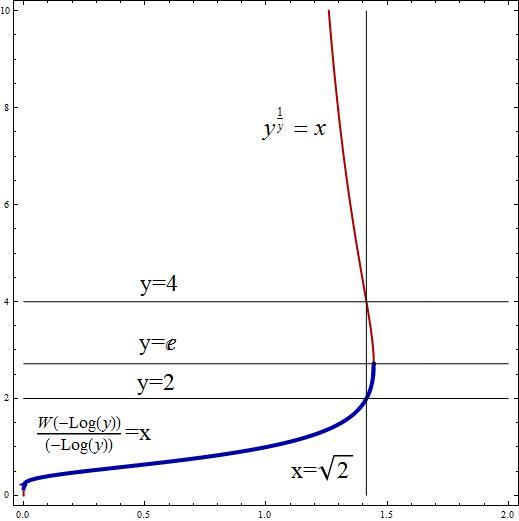
The thick blue graph is the actual infinite tetration function, which has the maximum value of $e$ , while the red graph is the implicit function ${ y }^{ \frac { 1 }{ y } }=x$ . The function $W(z)$ is the Lambert function, which is similar to the Log function, as follows

If ${ e }^{\displaystyle x }=y$ then $x=Log(y)$

If ${ xe }^{\displaystyle x }=y$ then $x=W(y)$

Both the blue and red functions match exactly right up to where the blue function terminates at $\left(\displaystyle { e }^{ \frac { 1 }{ e } },e \right)$ . However, as the blue function approaches $x=0$ at the other end, the story gets more complicated. See

Infinite Tetration

It does happen from time to time in mathematics that two different functions can have a perfect match part of the way,and then suddenly take off in different directions. And that's without even using the absolute value function, e.g. $\left| f(x) \right|$ . Just because two function "agree" perfectly much of the way doesn't mean they'll agree all the rest of the way.

If you put in Windows calculator ${ \sqrt { 2 } }^{ { \sqrt { 2 } }^{ { \sqrt { 2 } }^{ ... } } }$ you can get $2$ , $4$ , $16$ , $256$ , $65536$ , etc. These are strangers results.

Victor Paes Plinio - 6 years, 7 months ago

You must be using a Windows calculator that I'm not familiar with. I just now used my own Windows calculator, and sure enough, the result progresses towards $2$ . that is eventually, I get ${ (1.414...) }^{ \displaystyle 2 }=2$

Michael Mendrin - 6 years, 7 months ago

Yes is it, and if you continue doing it, after a new power of $\sqrt{2}$ the value becomes more higher like ${ 2 }^{ { 2 }^{ { 2 }^{ ... } } }$ .

Victor Paes Plinio - 6 years, 7 months ago

Problems like this are the reason this is the best site on the internet _

Pratyush Pandey - 4 years, 8 months ago

John M.
Oct 14, 2014

"John, simply put, the infinite tower can never have a value like 16. It doesn't matter what you have in the infinite tower, you just can't get up there. Just like in relativistic physics, there's a speed limit of c, infinite towers have a limit of e. OR it is immediately infinite right after x=e^(1/e)"

-Michael Mendrin, 4STD, October 12, 2014, Milky Way, Orion Ring, Sol, Earth, USA.

To support this, just out of myself, think about p-series sums; whenever $p$ is not greater than 1, it always diverges, starting at $p=1$ - the Harmonics. So I guess this is something of sort... Just not sums, or products, but this time exponentiation itself.

Another reason why $e_{coolness}>\pi_{coolness}$ .

Does "4D" stand for 4 dimensions?

Brian Charlesworth - 6 years, 8 months ago

4th Dimension.

Oh, and thanks for notifying - I added a clarification.

John M. - 6 years, 8 months ago

In that case, can we start referring to Michael as a Time Lord? I'm sure he'll appreciate that. :P

Brian Charlesworth - 6 years, 8 months ago

@Brian Charlesworth – Um, no, 4STD just means he lives in the 4th Space-Time dimension (because if it's time-space we'd have 3Ds of time and 1D of space - yeah there's such thing) - but sure, that'd be cool.

I personally refer to him as Mr. Mathopedia. I think that's on point xD

John M. - 6 years, 8 months ago

@John M. – Multiple dimensions of time? Holy eigenvalue, Batman! This sounds like a recipe for parallel universes. And here I thought that Godel proved that time does not exist. Apparently I have some reading up to do.

Brian Charlesworth - 6 years, 8 months ago

@Brian Charlesworth – Oooh you just like to trigger my philosophical spectrum, don't you!

Well, one can argue that the PASSAGE OF TIME is an illusion, but one cannot deny (unless stubbornly) the essential existence of it. A difference between the two, but yes, there's Time-Space vs. Space-Time. And after 6th D we introduce a new parameter other than time - I think, I'm not quite sure whether there is and what it is. And actually most of it is my speculation which makes sense to me, but I've built most of my repertoire from my own imagination and analysis of the 10th Dimension movie (which I've been advertising so much). I think the 7th D+ parameter is Energy - and trust me, I can argue real quick below how Energy is EVERYTHING.

Here we go:

Energy $\rightarrow$ Matter + Force

Matter + Force $\rightarrow$ Entropy

Entropy $\rightarrow$ Information

Information $\rightarrow$ Time

Time $\rightarrow$ Space

Space $\rightarrow$ Energy.

Space + Time + Information + Entropy + Matter + Force = Everything (in a real, 4D brane universe, that is).

BAM!

Did I lose you on any step there? Of course I did. That's alright, ask all ya want (but don't expect a timely reply ;))

John M. - 6 years, 8 months ago

@John M. – It doesn't take much to get you off and running with big thoughts; I admire that quality. :)

The "Entropy -> Information -> Time" is the fascinating one; Quantum Information Theory seems to be the coolest kid on the block right now. And yes, it all comes down to energy, whatever that may actually be.

P.S.. Thanks for the link to the 10D movie; a lot of speculation but really entertaining and thought provoking.

Brian Charlesworth - 6 years, 8 months ago

@Brian Charlesworth – Whether or not one wants to use the concept of time when doing physics is a matter of choice. It isn't absolutely necessary to have time as one of the physical dimensions. But I guess most people wouldn't know this.

Edit: Look up "Wheeler-DeWitt Equation"

Michael Mendrin - 6 years, 8 months ago

@Michael Mendrin – .... including me, apparently. Time as a choice, and not a necessity? I thought that quantum entanglement and the consequent diffusion of states made time unavoidable, or have I got this the wrong way 'round?

Is Godel's theory that time does not exist in a universe governed by the Theory of Relativity then imply that time is simply a variable of convenience that can be tossed away like a Lagrange multiplier after having served its purpose, and which, given other methods, was never necessary in the first place? My interest is piqued ..... but more mundane tasks beckon.

Brian Charlesworth - 6 years, 8 months ago

@Michael Mendrin – Thanks for the reference. It's a revelation that a mathematical framework can be established without requiring time as a variable, but intuitively dissatisfying. I know that common intuition has nothing to do with the pursuit of a GUT, but time, whatever it may be, has to be accounted for at some point, doesn't it?

Brian Charlesworth - 6 years, 8 months ago

@Brian Charlesworth – In theoretical-physics-speak, time is thought to be an "emergent property", along with other things like space and mass. I think what's hard for laymen to understand is that many theories or models in theoretical physics are interchangeable, i.e., you can kind of pick and choose which mathematically equivalent interpretation you want to go with, and you wouldn't necessarily be wrong. I think many people think "there can only be one truth, and everything else should be identified and shot in the alley!" In theoretical physics, at least, it doesn't work that way.,

Also see Julian Barbour's "End of Time". But his conclusion that "time doesn't exist" isn't exactly on target. He's just shown another way to do physics without it, but there's nothing wrong with doing physics with it.

Michael Mendrin - 6 years, 8 months ago

@Michael Mendrin – To do physics without time?? This must be one hella physics he's discussing...

You see, if anyone finds a way to do physics without time, I'd give them big kudos. But to me, this seems absurd; to discount time is to discount change, and the study of physics without the study of change must be the study of static physics, which, of course, noone really cares about.

So yeah... Tell me if he can describe an event over which change occurs but no time is involved...

John M. - 6 years, 8 months ago

@John M. – Okay, to get the gist of the idea of how it's possible to consider "change without time", think of a Platonic universe of mathematics , all the equations, geometry, etc., all interrelated in abstract ways. Certainly it looks different from idea to concept to abstraction, doesn't it? But we don't have to have physical dimensions such as time, space, or mass to consider or understand such a Platonic universe. Time is simply an emergent property, i.e., it's useful to have in analyzing a wide range of practical physics. But it'd be misguided to believe that time is necessary . A lot of theoretic physicists are real busy these days trying to figure out how things like space and time "emerged", and, no, this is not one and the same thing as the concept of the Big Bang, although they are certainly related.

Michael Mendrin - 6 years, 8 months ago

@Michael Mendrin – Actually I'd say that the principal definition of time is the measure of change. This is how I derived planck's time constant (without knowing it existed first): all change happens through motion - or - variations in patterns of matter in space (or space in space). Kinetic energy - the most fundamental type of energy - energy of motion. And so, planck's time is defined as the amount of time it takes light to travel one planck length. Why? Because this is the shortest time. Why? Because no change can be observed - no variation in pattern of matter or space in space - over any interval shorter than this. Any time shorter and the universe is still - there is no change - that is, till this much time passes (so sure go ahead and study static physics - you don't need time to describe how hard I'm pushing an object over a time interval shorter than planck's length. "but wait a minute, how is this possible? how can you measure something static?" - as in an "instantaneous quantity"? Well, let's thank Newton and Leibniz we can compute such things.)

So if time is a measure of change, then no non-static physics can exist without incorporation of time.

Argue against that, Mr. Mathopedia!

John M. - 6 years, 8 months ago

@John M. – Sure, I'll argue against that. This tetration problem, it involves 4 double steps, leading to some absurd conclusion. That's change from the first equation the last. Do we need time or space for such "changes"? No, we don't. You might try to argue that it takes "intelligent beings" operating in time and space to even think of those things, but "those things" are abstract realities "that are" without anyone or anything thinking them. That's the whole idea of Platonism, but I was using that concept only as an analogy. The point is, while it's useful to start with time and space, we don't have to, if we'd rather not, and still come up with useful physics.

Michael Mendrin - 6 years, 8 months ago

@Michael Mendrin – um... uhh... sorry but that analogy seems too far off. it's almost like trying to explain airplane dynamics with paper airplanes.

Remember "IMPOSSIBLE" ? Remember Rule #3? Yeah, I got that issue here. Math is abstract and is only used to describe Physical phenomenon. But math $\neq$ universe. Prof. Martin Lewin argued in one of his lectures that there are three fundamental quantities in physics: Length, Mass, Time. Well, I'll say he got his ass covered from all sides with those three. I liked to define our universe as Space-Time-Matter-Energy universe. Then I heard about $E=mc^2$ . So then it changed to Space-Time-Energy universe. And then I realized that's not what E=mc^2 means and changed back. And now above I argued simply - Energy. But I think I'll put back matter in there. Motion can be of non-material entities as well.

oh look I digressed.. Anyway, look at kinetic energy - mv^2. v = d/t. t. t. t. t. t. t. t. T!!! NO ENERGY = NO CHANGE. NO CHANGE = NO TIME. wait... why am I even... NO ENERGY = NO PHYSICS.

QUOD ERAT DEMONSTRANDUM.

John M. - 6 years, 8 months ago

@John M. – We really should continue this elsewhere. But I do want to point out to you that I said I'm using the "Platonic universe of mathematics" only as an analogy. Anyway, none of anything I said here is something I made up---those are all the things already being seriously discussed among theoretical physicists. If you like theoretical physics, you should at least be familiar with the ideas being floating around currently.

Michael Mendrin - 6 years, 8 months ago

@Michael Mendrin – I'm laughing at how this thread started with my simply asking what John meant by the "4D" he wrote after your name. :) Anyway, I'm beginning to warm to the notion that time is a convenient but not necessary variable. I can see how there can be "change" in a "static" universe by way of a semantic shift. However, the question that I'm dwelling on at this instant is: In a timeless paradigm, where all times are equally real, (or unreal), is the present no longer the intersection of the past and future but rather the portal to all that has ever existed? Is time travel not so far-fetched then? The old saying, "The more things change, the more they stay the same", takes on an added dimension, (sorry, puns are unavoidable in this conversation).

I've fished out a special edition of Scientific American devoted entirely to "A Matter of Time" to help me make some sense of all that has been discussed here. Perhaps it would be best if one of us posted a note titled "Time Matters?" (or whatever) and continued the conversation there so that others can jump in as well.

Brian Charlesworth - 6 years, 8 months ago

@Brian Charlesworth – I think that would be a good idea. I hope it's within the Brilliant format to occasionally have speculative talk, separate from problem-solving. We'll get back to this later.

Michael Mendrin - 6 years, 8 months ago

@Michael Mendrin – Yeah I did extremize myself but for sake of argument.

No pun intended.

Cheers

John M. - 6 years, 8 months ago

@Brian Charlesworth – Oh and just really briefly on how 7th dim could add the energy parameter:

So, we know Time operates on Space in an STD.

4th D - 1D timeline represents 3D space.

5th D - 2D phase space (plane time) represents 3D space.

6th D - 3D block time (cube time) represents 3D space.

(NOTE: Some people will say that instead of, per say, 2D timeline rep. 3D space, it's 2nd D timeline representing 4D space - that is, time is always the uppest dimension. But I think you could pretty much say they're mathematically equivalent - ask Mr. Mathopedia about this - I got nothing (but speculative words).

7th D - a new dimensional operator is introduced - whereas before space and time were being modified, now the universal constants are being modified. The 3Ds of time and 3Ds of space are condensed into a single point and stacked into a line (as it happened at the 4th D - space condensed into a single point and were stacked into a 1D timeline). So all previous dimensions are treated as a point and lined. And so, what can vary? Well, the space and time properties will vary with the universal constants for top speed, force, etc. In other words, ENERGY.

At the 10th D, 7, 8 (the higher dimensions just allow a broader range of possibilities for combinations of cosmic property distributions), and 9D are represented by a single point. And for some reason in the 10th dim vid that point isn't lined. But I guess that's how they accept it (dunno why).

So the string theory must line those 10th D points. Hence the multiverse theory.

okie I hope your head is intact. But me gots to go.

CHEERS!

John M. - 6 years, 8 months ago

@John M. – String Theory - Easy Peasy. :) Thanks for the summary. I felt like a 13-year old when I saw "STD" and laughed, but then I thought of the joke that Time is an STD - Spatially Transmitted Disease. :P Yeah, sorry, but I can't resist a pun to save my life.

Brian Charlesworth - 6 years, 8 months ago

In reality what you are proving there is that 2 infinity=4 infinity The problem has no solution since the infinite powers don't converge for any value >1.

Javier Montejo - 6 years, 7 months ago

Yeah they do.

See this

John M. - 6 years, 7 months ago

They don't, that's actually the problem I'm referring to. The LHS tends to infinity for x>1 and therefore that equation is not fulfilled for any value of x.

Javier Montejo - 6 years, 7 months ago

@Javier Montejo – Well this really isn't subjective...

You can see Mr. Mendrin's reasoning above, as to how the value of $x$ may not exceed $e^{1/e}$ , but anything less than that in magnitude is fine (including $\sqrt{2}$ ).

Alternatively, you can try raising $sqrt{2}$ into itself more and more times on WolframAlpha and see what happens (I gave you a head start).

Cheers

John M. - 6 years, 7 months ago

@John M. – My apologies, I had scripted the problem (with a bug) and I saw it diverging for √2. After some thoughts/scrabbling I agree with all that has been previously said about this. Cheers

Javier Montejo - 6 years, 7 months ago

Ekene Franklin
Aug 25, 2018

The maximum value possible in an infinite tetration is the Euler number e.

Ameya Anjarlekar
Aug 31, 2016

Lst given value be x Taking log on both sides 2logx=xlog2 x=4 doesnt satisfy

Aaaaaa Bbbbbb
Oct 14, 2014

Because: $x^{x^{x*{...}}}=y$ when $x != y^{1/y}$

Proof That 2 = 4

6 solutions

0 pending reports