Proof Without Words

Algebra Level 3

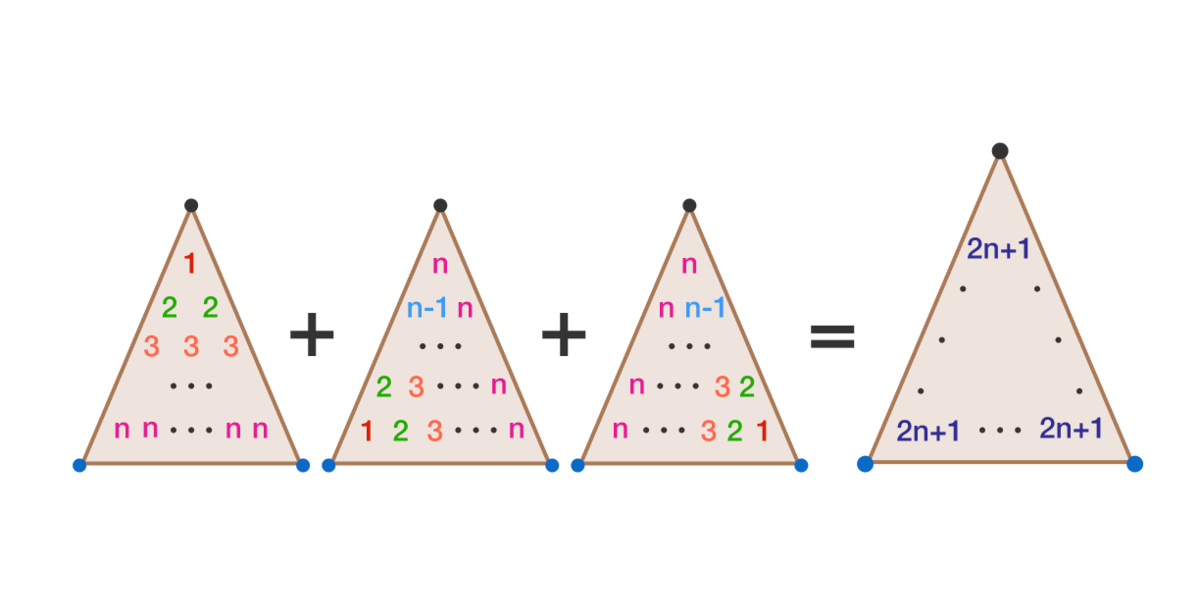
What is represented in the above image?

1^3 + 2^3 + 3^3 + \cdots + n^3 = \frac{1}{4} n^2(n+1)^2

1^2 + 2^2 + 3^2 + \cdots + n^2 = \frac{1}{6} n(n+1)(2n+1)

1 + 2 + 3 + \cdots + n = \frac{1}{2} n(n+1)

1 + 3 + 5 + \cdots + (2n+1) = (n+1)^2

1 solution

Michael Mendrin
Feb 6, 2017

Boy, that was really cute. Maybe no words were needed, but maybe a lot of squinting at the graphic was needed.

First, each triangle is the sum of squares ${1}^{2}+{2}^{2}+{3}^{2}+...+{n}^{2}$ . There's $3$ such triangles, they are all the same thing through rotation.

Thus the elements of the final triangle are all $2n+1$ . $\;$ A quick way to visualize why is to imagine $3$ planes dipped at the same angle relative to the $xy$ plane but rotated about the $z$ -axis $120$ degrees apart---the sum of the $3$ planes will be parallel to the $xy$ plane.

The number of elements in any of the triangles is $\dfrac{1}{2}n(n+1)$ . $\;$ Multiply that by $(2n+1)$ and then divide both sides by $3$ to get

${1}^{2}+{2}^{2}+{3}^{2}+...+{n}^{2}=\dfrac{1}{6}n(n+1)(2n+1)$

Now that I see this, I don't think I can unsee it. That's an easy way to remember the formula for the sum of consecutive squares.

Would colors on 1, 2, 3 help make them easier to identify / less squinting involved?

Calvin Lin Staff - 4 years, 4 months ago

Check out graphic I've put together

Michael Mendrin - 4 years, 4 months ago

A quick way to visualize why is to imagine 3 planes dipped at the same angle ...

Currently, my favorite way is to relate it to a ternary plot .

Calvin Lin Staff - 4 years, 4 months ago

A favorite among chemists! That was my first experience with them.

Here, with this problem, the crux is that the coefficients are a linear function of its position.

Michael Mendrin - 4 years, 4 months ago

Yep, you presented one way of comprehending this. But there's yet another interpretation which is currently one of the proposed solutions and is much more simple. Actually what we see here is a demonstration of the number of ways to add 3 positive integers less equal n such that the sum shall be 2n+1. There are n(n+1)/2 such options... - these are the number of items in each of the triangles. So the minute no words are said – there's yet another comprehension of the problem.

Aviel Livay - 4 years, 4 months ago

I think a ternary plot would illustrate that, as Calvin has noted. All the possible ways positive integers can add up to 2n+1.

Michael Mendrin - 4 years, 4 months ago

My point is that answer (a) : 1/2*n(n+1) is a correct answer. And of course answer (b) as well. Perhaps brilliant should expand the options and suggest (a)+(b) are correct and such.

Aviel Livay - 4 years, 4 months ago

@Aviel Livay – All of the options are true equations.

The question is "What is represented in the above image". In order for $1 + 2 + ... + n = \frac{1}{2} n (n+1)$ to be a correct answer, can you explain why (from the diagram) "the sum of the first n integers" is equal to "the number of ways $a + b + c = 2n + 1$ , and finally how you knew that "there are $\frac{ n(n+1) } { 2 }$ such options.

Calvin Lin Staff - 4 years, 4 months ago

@Calvin Lin – How did I know that there are n(n+1)/2 options for adding 3 positive integers that are smaller equal n such that their sum is 2n+1? I imagined 3 compartments and then I put 1 ball in each compartment, because there must be at least 1 in each compartment. Then I was left with 2n-2 balls and 3 compartments – number of options here are 2n*(2n-1)/2 = n(2n-1) But this number contains also the option where in the left compartment we shall put n or n+1 or n+2 etc on top of the first ball – this should not be counted. So I run k from n to 2n-2 and the sum of the two other compartments is 2n-2-k, the number of options is 2n-2-k+1. I actually sum n-1 + n-2 + … + 1 which give (n-1)n/2. But this is only for the left compartment – we should multiply this by 3… - so we get 3(n-1)n/2 Now to summarize we have n(2n-1)-3(n-1)n/2=0.5n^2+0.5n=n(n+1)/2

Now your other question is how we can see it from the diagram. Here’s the answer. You look at the top, left has 1, middle has n and right has n. This first row contains all the options for a sum of 2n+1 when the first number is 1. Going to the second row. Now we shall see the number of options to get a sum of 2n+1 when the first number is 2. This time there are obviously 2 options: 2+(n-1)+n & 2+n+(n-1). Then as we move on of course that the next row the first number has 3 so now there are 3 options. So we actually get 1 + 2+ 3 + … n = n(n+1)2/.

Aviel Livay - 4 years, 4 months ago

@Aviel Livay – The bijection is a great observation to make ! I think this is my first time seeing it.

The problem asks "What is represented in the above image?". The issue of "how do we use the image (as it is) to obtain the value of $\frac{n(n+1) } { 2}$ ?" still remains.

Currently, it seems to me (and I might be wrong) that you are either
1. Using a different argument to explain why this is true (e.g. relying on your first paragraph)
2. Using the fact that $1 + 2 + 3 + \ldots + n = \frac{ n(n+1) } { 2}$ to prove it (e.g in your first paragrpah, you use the fact that "I actually sum n-1 + n-2 + … + 1 which give (n-1)n/2" to prove that "the sum is n(n+1)/2". Also, in your second paragraph you say "So we actually get 1 + 2+ 3 + … n = n(n+1)/2", where (to me) the RHS value of n(n+1)/2) hasn't been justified within that paragraph)

(This is a new step that I'm introducing, to help bolster your claim)

Interpret the image as "find the number of ordered triplets of $1 \leq a, b, c, \leq n$ to $a + b + c = 2n+ 1$ ". Then, the number of solutions is represented by the LHS . We see that corresponding to when $a = 1, 2, 3, \ldots, n$ , there are $1, 2, 3, \ldots, n$ solutions. Hence, the total number of solutions is $1 + 2 + 3 + \ldots + n$ .

Calvin Lin Staff - 4 years, 4 months ago

Proof Without Words

1 solution

0 pending reports