Proximity to perfect squares

The first observation one should make is that this function has a special symmetry around square numbers. Take a look at the following values of the series:

$\sum_{n=1}^{\infty} \frac{f(n)}{n} = \frac{1}{2} - \frac{1}{3} + \frac{1}{5} + \frac{1}{6} - \frac{1}{7} - \frac{1}{8} + \frac{1}{10} + \frac{1}{11} + \frac{1}{12} - \frac{1}{13} - \frac{1}{14} - \frac{1}{15} + ...$ . If we group the terms that occur before the sum reaches perfect squares we get the following:

$\sum_{n=1}^{\infty} \frac{f(n)}{n} = \sum_{k=1}^{\infty} \left( \sum_{n=1}^{k} \frac{1}{k^2 + n} - \sum_{n=1}^{k} \frac{1}{(k+1)^2 - n} \right)$ . This is basically a new infinite series that is equivalent to the previous one but has the property that every term of the infinite sum is a positive one. With this, we can start bounding. Notice that:

$\sum_{k=1}^{\infty} \left( \sum_{n=1}^{k} \frac{1}{k^2 + n} - \sum_{n=1}^{k} \frac{1}{(k+1)^2 - n} \right) \leq \sum_{k=1}^{\infty} \left( \sum_{n=1}^{k} \frac{1}{k^2 + 1} - \sum_{n=1}^{k} \frac{1}{(k+1)^2 - 1} \right) = \sum_{k=1}^{\infty} \frac{k}{k^2 + 1} - \frac{k}{(k+1)^2 - 1} = \sum_{k=1}^{\infty} \frac{2k - 1}{k^3 + 2k^2 + k + 2} \leq \sum_{k=1}^{\infty} \frac{2k}{k(k+1)^2} = \sum_{k=1}^{\infty} \frac{2}{(k+1)^2} = \frac{1}{3} \left( \pi^2 - 6 \right) \approx 1.289...$

For the last equality I used the known result that $\sum_{k=1}^{\infty} \frac{1}{k^2} = \frac{\pi^2}{6}$ .

---

Using a computer to compute this sum up to the 1000000th term I got $0.542513834759228$ but the convergence is very bad. I can at least say that $0.54...$ are true digits of the real value.

---

I added up to $10^{12}$ terms to find $0.543512334760729...$ and now I can confirm the digits up to $0.543512...$

Note that $\begin{aligned} X_n \; = \; \sum_{j=n^2-n+1}^{n^2+n} \frac{f(j)}{j} & = \; -\sum_{j=1}^{n-1} \frac{1}{n^2-j} + \sum_{j=1}^n \frac{1}{n^2+j} \\ & = \; \frac{1}{n(n+1)} + \sum_{j=1}^{n-1}\left(\frac{1}{n^2+j} - \frac{1}{n^2-j}\right) \; = \; \frac{1}{n(n+1)} - 2\sum_{j=1}^{n-1}\frac{j}{n^4-j^2} \end{aligned}$ for all integers $n \ge 2$ . Note that $2\sum_{j=1}^{n-1}\frac{j}{n^4 - j^2} \; \le \; 2\sum_{j=1}^{n-1} \frac{j}{n^4 - n^2} \; = \; \frac{n(n-1)}{n^2(n^2-1)} \; = \; \frac{1}{n(n+1)}$ for all $n\ge 2$ , so we deduce that $0 \le X_n \le \frac{1}{n(n+1)}$ for all $n \ge 2$ . Since $\sum_{j=1}^{n^2+n}\frac{f(j)}{j} \; = \; \frac12 + \sum_{m=2}^n X_m$ we deduce that $\sum_{j=1}^\infty \frac{f(j)}{j}$ is convergent, with limit less than $\tfrac12 + \sum_{m \ge 2} \tfrac{1}{m(m+1)} = 1$ . Certainly, then, the limit is less than $2$ .

To be picky, if we denote $S_n = \sum_{j=1}^n \frac{f(j)}{j}$ , we have so far shown that the subsequence $S_{n^2+n}$ converges to some limit as $n \to \infty$ . Since $\big|S_m - S_{n^2+n}\big| \; \le \; \sum_{j=n^2-n+1}^{n^2+n} \frac{1}{j} \; \le \; \frac{2n}{n^2 - n + 1} \le \frac{2}{n-1} \hspace{2cm} n^2-n+1 \le m \le n^2 + n$ we can now deduce that the entire sequence of partial sums $S_m$ converges.

If the limit is $L$ , then $0 \le L - \sum_{j=1}^{n^2+n} \frac{f(j)}{j} \; = \; \sum_{m=n+1}^\infty X_m \; \le \; \frac{1}{n+1}$ and hence we deduce that the error term $L - \sum_{j=1}^n \frac{f(j)}{j}$ tends to $0$ as $n \to \infty$ no faster than $n^{-\frac12}$ .

Let's group the terms around a perfect square $\frac{1}{n^2}$ .
$\sum_{n=1}^{\infty} \frac{f(n)}{n} = (\frac{1}{2}) +(- \frac{1}{3} + \frac{1}{5} + \frac{1}{6}) +( - \frac{1}{7} - \frac{1}{8} + \frac{1}{10} + \frac{1}{11} + \frac{1}{12}) +( - \frac{1}{13} - \frac{1}{14} - \frac{1}{15} + \frac{1}{17} + \frac{1}{18} + \frac{1}{19} + \frac{1}{20} ) + \ldots$ .
In each group, we subtract off $n-1$ terms that are larger than $\frac{1}{n^2}$ , and add on $n$ terms that are smaller than $\frac{1}{n^2}$ . Thus, the total sum will be less than $- (n-1) \times \frac{1}{n^2} + n \times \frac{1}{n^2} = \frac{1}{n^2}$ .

Hence, we can conclude that

$\sum_{n=1}^{\infty} \frac{f(n)}{n} < \frac{1}{1} + \frac{1}{4} + \frac{1}{9} + \ldots = \frac{\pi^2}{6} \approx 1.644$

We can tighten up the bound by accounting for the initial terms. For example,

$\sum_{n=1}^{\infty} \frac{f(n)}{n} < \frac{1}{2} + \frac{1}{4} + \frac{1}{9} + \ldots = \frac{1}{2} + \frac{\pi^2}{6} - 1 \approx 1.144$
$\sum_{n=1}^{\infty} \frac{f(n)}{n} < \frac{1}{2} - \frac{1}{30} + \frac{1}{9} + \ldots = \frac{14}{30} + \frac{\pi^2}{6} - (1 + \frac{1}{4}) \approx 0.86$
$\sum_{n=1}^{\infty} \frac{f(n)}{n} < \frac{1}{2} - \frac{1}{30} - \frac{59}{9240} + \ldots = \frac{4253}{9240} + \frac{\pi^2}{6} - (1+\frac{1}{4} + \frac{1}{9}) \approx 0.74$
The next line (too ugly to write out) is $< 0.68$ and the line after that is $< 0.64$ .

---

Note: We can improve the bounding of each group. As Alexander Maly shows in the comments, each parenthesis is very slightly larger than $\frac{1}{2 n^ 4}$ . $\frac{ \zeta (4) } {2 } \approx 0.5411$ , which is much closer to the true value.

Using symmetry, you can figure that it must be smaller than a certain number, which could eventually be figured as 2.

You can solve this intuitively. Square numbers add nothing to f(n) so all we are concerned with is the distance between consecutive, perfect squares.

If you take the distance between any two very large, consecutive, perfect squares and tally all of the scenarios resulting in (1)s and (-1)s you will notice that the tallies differ by at most 2. Let's say that we have a distance of 1,000,000 between two arbitrary perfect squares, the first 499,999 are (1)s and the last 500,000 are (-1)s, there is now a 50/50 chance that our last number is either a (1) or (-1). Regardless of who gets the tally, the percent total of each tally will be approximately 50%, and will continue to get closer to exactly 50% so we can deduce that the function converges somewhere around .5

I don't know if my deduction is correct but what i thought is that, as the denominator keeps getting bigger and the numerator go from -1 to 1, it's not able to get higher than 2

We write the series as:

$S=(\frac{1}{2}-\frac{1}{3})+(\frac{1}{5}+\frac{1}{6}-\frac{1}{7}-\frac{1}{8}) \cdots = \sum\limits_{k=1}^{\infty} \sum\limits_{n=1}^k (\frac{1}{k^2+n}-\frac{1}{k^2+k+n}) = \sum\limits_{k=1}^{\infty} \sum\limits_{n=1}^k \frac{k}{(k^2+n)(k^2+k+n)}$

Since $n> 0$ ,

$\frac{k}{(k^2+n)(k^2+k+n)}< \frac{k}{k^2(k^2+k)}$

Therefore,

$S < \sum\limits_{k=1}^{\infty} \sum\limits_{n=1}^k \frac{k}{k^2(k^2+k)} = \sum\limits_{k=1}^{\infty} \frac{k^2}{k^2(k^2+k)}= \sum\limits_{k=1}^{\infty} \frac{1}{k(k+1)} = 1$

So $S$ converges to a value smaller than 1.

We can see that between two adjacent squared integers $n, n+1$ , there are exactly $2n$ integers. Half of them will contribute to the series with a plus sign, while the rest will get a minus sign. We can thus write the series as:

$\sum_{n=1}^{\infty} \left( \sum_{k=1}^n ( \frac{1}{k+n^2}- \frac{1}{k+n^2+n} ) \right)$ We can express the above nested sum in terms of the digamma function $\psi(x)$ , making use of the properties appearing in Digamma function , like $\psi(x+N)- \psi(x) = \sum_{k=0}^{N-1} \frac{1}{x+k}$ . We have: $\sum_{n=1}^{\infty} \left[2\psi(1+n+n^2)-\psi(1+n^2)-\psi(1+2n+n^2) \right]$ We can then approximate the digamma function by: $\psi(x) \approx ln(x)-\frac{1}{2x}+ \mathcal{O}(1/x^2)$ , which gets better and better as we sum over larger integers. We can drop the logarithmic behaviour, since for large n, all three functions behave as $2ln(n)$ . So $\sum_{n=1}^{\infty}\frac{f(n)}{n} \approx \sum_{n=1}^{\infty} \left( \frac{1}{2(n^2+1)}-\frac{1}{1+n+n^2}+\frac{1}{2(1+2n+n^2)} \right)$ If you work out the fractions, you can see that $\sum_{n=1}^{\infty}| \frac{f(n)}{n}| < \sum_{n=1}^{\infty} \frac{1}{n^3}= 1.20206$ . The series is thus bounded by above and converges to a number smaller than 2

Kind of stupid approach: ask computer to calculate first 1000 sums

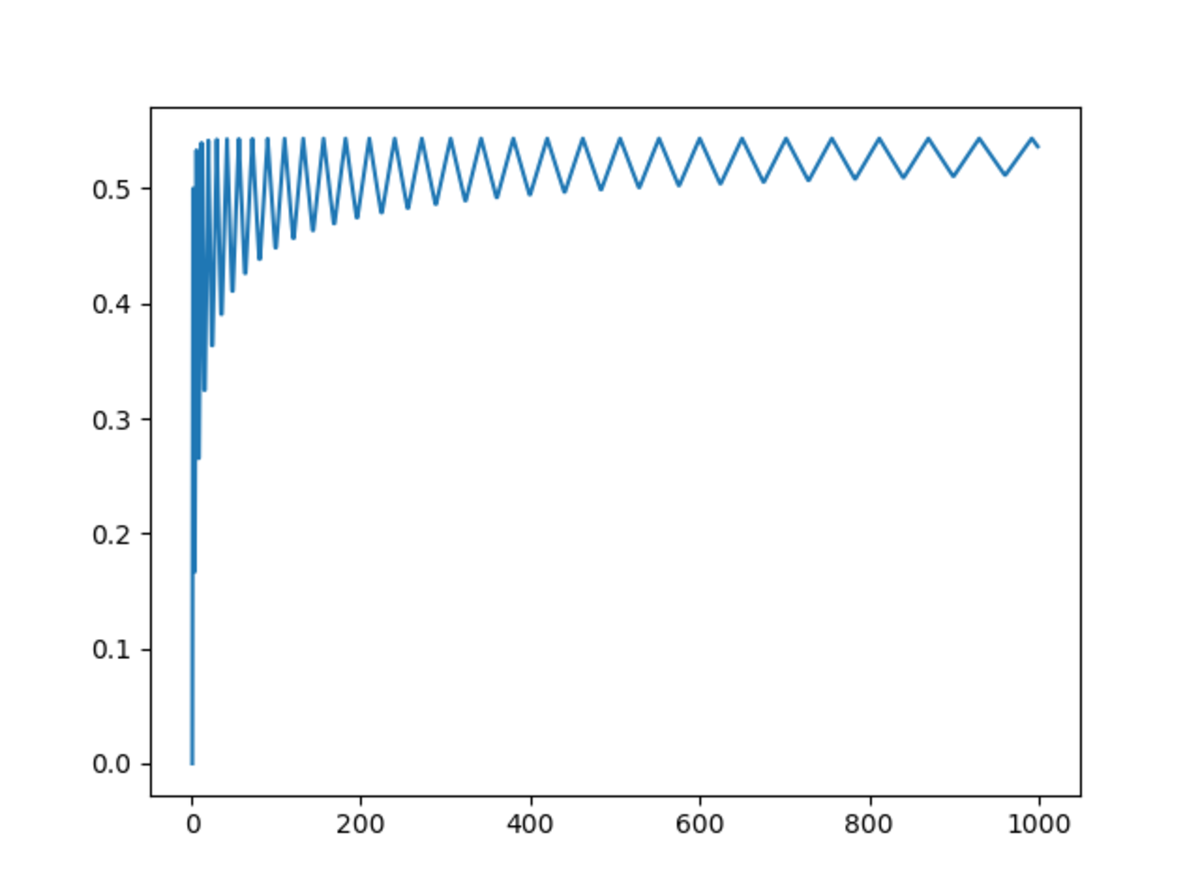Obviously converges to something around 0.5

Code