A geometry problem by Worranat Pakornrat

Geometry Level 4

Consider all sets of 4 points $A, B, C, D$ which satisfy the following conditions:

$AB$ is an integer.
$BC = AB + 1$ .
$CD = BC + 1$ .
$DA = CD + 1$ .
$AC= DA + 1$
$AC$ divides $AB \times CD + BC \times DA$ .

Over all such sets, what is $\max \lceil BD \rceil ?$

The answer is 13.

2 solutions

Worranat Pakornrat
Apr 19, 2016

Relevant wiki: Ptolemy's Theorem

According to Ptolemy's theorem, for any quadrilateral, the product of the diagonals will be less than or equal to the sums of the products of the opposite sides:

$(AB\times CD) + (BC\times DA) \geq AC\times BD$

Now let $AB = x$ and $BD = n$ for some positive integers $x$ & $n$ .

Then $x(x + 2) + (x + 1)(x + 3) \geq (x + 4)n$ .

$n(x + 4) \leq x^2 + 2x + x^2 + 4x + 3 = 2x^2 + 6x + 3$

$n \leq \dfrac{2x^2 + 6x + 3}{x + 4} = (2x - 2) + \dfrac{11}{x + 4}$

Since $n$ & $x$ are positive integers, $\dfrac{11}{x + 4}$ must also be an integer. Thus, $x = 7$ .

As a result, $n \leq (14 - 2) + 1 = \boxed{13}$ .

Therefore, the upper bound of $BD$ is $13$ in such constraints.

Moderator note:

Given all of the discussion, can you update the solution to reflect what you have learnt?

I believe that $BD = 13$ cannot be achieved.

It is not clear to me what is happening here.

I don't get this. Why does $\frac{11}{x+4}$ have to be an integer?

Clearly, $n=13$ isn't the solution, as Mr Mendrin demonstrated: There is no quadrilateral with dimensions $7,8,9,10; 11,13$

Otto Bretscher - 5 years, 1 month ago

Of course, sir, those dimensions do not exist. That's why I adjusted 13 to be the least upper bound of $BD$ instead.

Worranat Pakornrat - 5 years, 1 month ago

But if you drop the condition of the diagonal BD being of integer length, then you can make it as long as you wish by making AB as long as you wish... there is no upper bound.

I'm afraid this problem still makes little sense.

Otto Bretscher - 5 years, 1 month ago

@Otto Bretscher – Well, sir, but if we retain the condition of the least upper bound $BD$ being the integer (instead of the diagonal $BD$ itself), shouldn't the solution be unique in Ptolemy's inequality?

Worranat Pakornrat - 5 years, 1 month ago

@Worranat Pakornrat – I'm afraid not. The larger you make AB, the larger BD will be... it will grow without bound.

Otto Bretscher - 5 years, 1 month ago

@Otto Bretscher – That I agree, but for example, if $AB = 1000$ , then $BD \leq (1000*1002 + 1001*1003)/1004 = 2006003/1004$ .

This least upper bound is not an integer in Ptolemy's inequality. My point is, there may be countless possibilities for $BD$ ; however, I'm trying to point out that there is only one least upper bound which turns out to be the integer in Ptolemy's inequality.

Worranat Pakornrat - 5 years, 1 month ago

@Worranat Pakornrat – Well, a least upper bound of the diagonal BD simply does not exist, integer or not..think about it (bed time for me... I hope this is all cleared up when I wake up in the morning ; )

Otto Bretscher - 5 years, 1 month ago

@Otto Bretscher – Well, what if we define it as "supremum" then, sir?

Worranat Pakornrat - 5 years, 1 month ago

@Worranat Pakornrat – As I have just commented in the reports section, there is only one cyclic quadrilateral with sides $a,b,c,d$ with $b=a+1$ , $c=a+2$ , $d=a+3$ and matching diagonal $p=a+4$ , and that does not have integer sides. You cannot make $q=BD$ arbitrarily big - the only value it can take is about $9.64661$ . Thus the least upper bound of $BD$ does exist, since there is only one value that it can take, and that value is not $13$ .

Noting that the question has removed the requirement for cyclicity, we can make the following observations. There is a unique convex quadrilateral with sides $a,b,c,d$ with $b=a+1$ , $c=b+1$ , $d=c+1$ and matching diagonal $p=d+1$ for any integer $a>3$ (the triangles $ABC$ and $ACD$ are unique). For this quadrilateral $\cos \angle BAC \; = \; \frac{a^2 + 6a + 15}{2a(a+4)} \qquad \cos \angle CAD \; = \; \frac{a+7}{2(a+4)}$ Both of these cosines tend to $\tfrac12$ as $a \to \infty$ and hence both angles tend to $60^\circ$ as $a \to \infty$ . Thus, for large enough $a$ , both angles are greater than $45^\circ$ , and hence $\angle BAD > 90^\circ$ . Since the triangle $BAD$ is obtuse-angled, it is clear that $BD > a$ . Since $a$ can increase without limit, so can $BD$ . Indeed, since the triangles $ABC$ and $ACD$ will become increasingly closer to being equilateral as $a\to\infty$ , the diagonal $BD$ will be approximately $a\sqrt{3}$ for large $a$ .

Thus the diagonal $BD$ has no supremum.

Your new proposed solution contains big logical problems. Once you move from equalities to inequalitities, your ability to deduce that (in your notation) $x+4$ divides $11$ is gone. In addition, just because there exist numbers $a,b,c,d,p,q$ such that $pq = ac + bd$ does not mean that a quadrilateral exists with these numbers as edge and diagonal lengths.

Mark Hennings - 5 years, 1 month ago

@Mark Hennings – OK, I think this time it will make everyone happy.

Worranat Pakornrat - 5 years, 1 month ago

@Otto Bretscher – Hm...how about we look at it this way? Let $A$ be the set of the segment ratios and set $B_{i}$ be the set of possible values of $BD$ as shown below and $N$ be the set of natural numbers and $AB = x$ .

$A$ = { $\dfrac{2x^2 + 6x + 3}{x + 4}$ : $x \in N$ ; $x > 0$ }

Let $a_{i}$ be the element in set $A$ and $B_{i}$ = { $b \in R^+$ : $b <$ $a_{i}$ }.

Thus, $sup({B_{i}}) = a_{i}$ .

There is only one element in $A$ that is an integer, so there is only one supremum of $B$ that is an integer: $sup({B_{7})} = 13$ .

Worranat Pakornrat - 5 years, 1 month ago

@Worranat Pakornrat – You are overthinking this problem; the situation is really quite simple, requiring only grammar school geometry. For every large positive integer $x$ there exists a unique convex quadrilateral with $AB=x,BC=x+1,CD=x+2,AD=x+3$ and $AC=x+4$ : Just start with $AC$ and then construct the sides. I keep repeating myself: As we let $x$ grow without bound, $BD$ will grow without bound as well.

Otto Bretscher - 5 years, 1 month ago

In my humble opinion this question still does not make sense. As we have discussed at length, there are only two quadrilaterals with the required properties, one of them convex with a "long(er)" diagonal $BD$ . The length of $BD$ in the convex case is easy to compute with basic geometry; it is $12<BD<13$ . It makes little sense to ask for some hypothetical "supremum" of $BD$ that is not actually attained in any quadrilateral.

One way to salvage the problem is this: Keep the question and the answer as is, but ask at the end: "... what is the least integer upper bound of the diagonal $BD$ ?" This would make the problem somewhat interesting and meaningful, although perhaps not in the way you intended.

Otto Bretscher - 5 years, 1 month ago

The way the problem is now phrased, we need to show that there exists such a quadrilateral with $BD>12$ .

Solving a biquadratic equation, we can see that the two possible values of $BD$ are $\frac{1}{11}\sqrt{10609\pm480\sqrt{390}}$ . The larger one, in the convex quadrilateral, is about 12.8848, showing that the least integral upper bound is indeed 13.

Otto Bretscher - 5 years, 1 month ago

OK, the author has found a question which has an answer of $13$ .

The length $BD$ of the only convex quadrilateral that satisfies the conditions is $12.88$ .

The question would be much better if it stated that the rectangle was convex, and simply asked for the ceiling $\lceil BD \rceil$ , rather than the rather clumsy "least integral upper bound of $BD$ ", given that there is only one value for $BD$ under these conditions.

Mark Hennings - 5 years, 1 month ago

I must confess that I rather like the way the problem is now phrased. At the very least, it seems formally correct.

Finding out that there are only two solutions (and only one convex one) is a big part of the problem, involving some algebra (to get to $AB=7$ and then some geometry. We might be giving too much away if we ask for the ceiling of the convex solution right away.

The term "least integral upper bound" is pretty widely used (I did a google search); whether it is clumsy is a matter of taste. Remember that most of us are not native English speakers, so, things might sound different to our ears.

Otto Bretscher - 5 years, 1 month ago

Michael Mendrin
Apr 20, 2016

Given a cyclic quadrilateral of successive sides 7,8,9,10, the lengths of the diagonals are actually $\sqrt { \frac { 10153 }{ 73 } }=11.7933...$ and $\sqrt { \frac { 10439 }{ 71} }=12.1255...$ , not $11$ and $13$ .

I don't know of a good way to fix this problem. If Ptolemy actually created such a cyclic quadrilateral, maybe we should have another look at what he did or said?

Since the discussion of this problem is already detailed, I will add the report I have just posted...

This quadrilateral cannot exist. Suppose there were a cyclic quadrilateral $ABCD$ with integer sides $AB=a,BC=b,CD=c,DA=d$ with $b=a+1$ , $c=a+2$ , $d=a+3$ , as well as integer diagonals $AC=p,BD=q$ with $p=a+4$ . Then Ptolemy's First Theorem would tell us that $(a+4)q \; = \; pq \; = \; ac + bd \; = \; a(a+2) + (a+1)(a+3) \; = \; 2a^2 + 6a + 3$ and hence $a+4$ must divide $2a^2 + 6a + 3 = 2(a+4)(a-1) + 11$ , so that $a+4$ must divide $11$ . Since $a$ is a positive integer and $11$ is prime, it follows that $a=7$ , $b=8$ , $c=9$ , $d=10$ , $p=11$ and hence $q=13$ .

However, the triangles $ABC$ and $ACD$ should share the same circumcircle as the cyclic quadrilateral $ABCD$ . A triangle with sides $u,v,w$ has circumradius $R \; =\; \frac{uvw}{\sqrt{(u+v+w)(u+v-w)(u+w-v)(v+w-u)}}$ Since $ABC$ has sides $7,8,11$ , it has circumradius $\frac{77}{\sqrt{195}}$ . Since $ACD$ has sides $9,10,11$ , it has circumradius $\frac{33}{4\sqrt{2}}$ . Thus the circumcircles of $ABC$ and $ACD$ are not the same, and hence $ABCD$ is not cyclic.

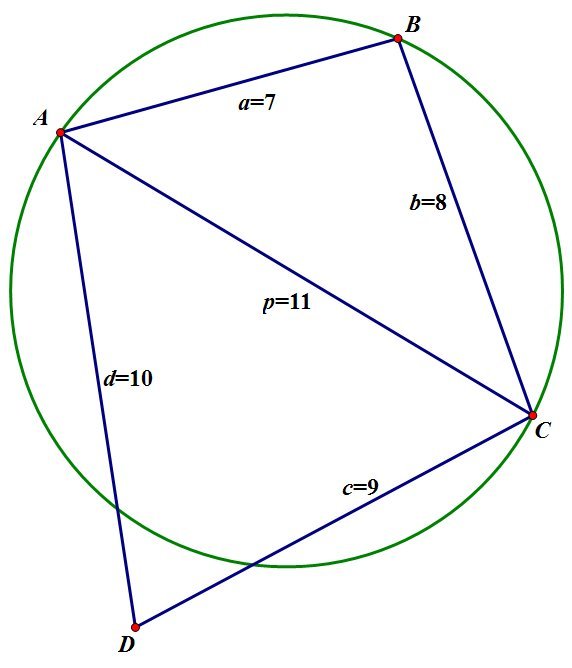
If we consider a quadrilateral with sides $a,b=a+1,c=a+2,d=a+3$ and diagonal $p=a+4$ , then $\begin{array}{rcl} \cos B & = & \displaystyle\frac{a^2 + (a+1)^2 - (a+4)^2}{2a(a+1)} \; = \; \frac{a^2 - 6a - 15}{2a(a+1)} \\ \cos D & = & \displaystyle\frac{(a+2)^2 + (a+3)^2 - (a+4)^2}{2(a+2)(a+3)} \; = \; \frac{a^2 + 2a - 3}{2(a+2)(a+3)} \end{array}$ If we want $ABCD$ to be cyclic, then $B + D = 180^\circ$ , and hence $\begin{array}{rcl} \cos B + \cos D & = & 0 \\ \displaystyle \frac{a^2 - 6a - 15}{2a(a+1)} + \frac{a^2 + 2a - 3}{2(a+2)(a+3)} & = & 0 \\ (a^2 - 6a - 15)(a+2)(a+3) + (a^2 + 2a - 3)a(a+1) & = & 0 \\ a^4 + a^3 - 20a^2 - 57a - 45 & = & 0 \\ (a + 3)(a^3 - 2a^2 - 14a - 15) & = & 0 \\ a^3 - 2a^2 - 14a - 15 & = & 0 \end{array}$ since $a$ must be positive. There is a unique real solution to this cubic equation, but the value of $a \approx 5.23$ is irrational.

We could salvage this problem by dropping the requirement for integer side lengths, and looking for the value $a = 5.23$ .

Mark Hennings - 5 years, 1 month ago

Thank you for your solution. I hope the new wording can help preserve the problem's contents.

Worranat Pakornrat - 5 years, 1 month ago

In reference to the first part of your post (before the figure), it is worth pointing out that a quadrilateral with the dimensions we want (7,8,9,10; 11,13) does not exist at all, cyclic or not.

Otto Bretscher - 5 years, 1 month ago

Could you please show us how you achieved these diagonals?

Worranat Pakornrat - 5 years, 1 month ago

The formulas for the length of the diagonals can be found here

Otto Bretscher - 5 years, 1 month ago

Thank you, sir. ;)

Worranat Pakornrat - 5 years, 1 month ago

Great observation, Mr Mendrin!

Otto Bretscher - 5 years, 1 month ago

Well, as I've noted in the View Reports section, what interests me about this problem is how easy it was to come to a fallacious conclusion. As how I imagine Worranat is wondering, "What went wrong?" Where did he go off the rails? I think the best way I can try to answer that is that if the quadrilateral is cyclic, and given the lengths of its four sides, then both diagonals are already fixed, and all we know about them is that the product follows Ptolemy's Theorem. Working them out is another matter. If we relax the condition that the quadrilateral is cyclic, then Ptolemy's Theorem cannot be used to find out anything, but fixing any one diagonal will uniquely determine the other.

Michael Mendrin - 5 years, 1 month ago

Looked at another way, it is a matter of reading implications. A cyclic quadrilateral has to satisfy Ptolemy's Theorem, but satisfying the equation of Ptolemy's Theorem does not guarantee a cyclic quadrilateral (a set of numbers $a,b,c,d,p,q$ that satisfy the equation in Ptolemy's Theorem does not have to correspond to an quadrilateral, cyclic or otherwise). The quadrilateral intended by the author does not satisfy Ptolemy's Second Theorem, which is another way of showing the problem to be wrong.

Mark Hennings - 5 years, 1 month ago

@Mark Hennings – Your statement is misleading: A quadrilateral that satisfies Ptolemy's Theorem does indeed have to be cyclic.

Otto Bretscher - 5 years, 1 month ago

@Otto Bretscher – Observe the bracketed clarification (added before your post). I stated that numbers that satisfy the equation do not have to define a cyclic quadrilateral - vide 7,8,9,10,11,13.

Mark Hennings - 5 years, 1 month ago

@Mark Hennings – Still, your statement that "a quadrilateral that satisfies Ptolemy's Theorem does not have to be cyclic" is false; it's hard to clarify a false statement ;) The "clarification" would be clearer if you said "...does not have to correspond to an actual quadrilateral", dropping "cyclic".

Otto Bretscher - 5 years, 1 month ago

@Mark Hennings – My apology for my mistake. I hope the new wording will help preserve the problem's contents and be more satisfying.

Worranat Pakornrat - 5 years, 1 month ago

Thank you for your solution. I hope the new wording can help preserve the problem's contents.

Worranat Pakornrat - 5 years, 1 month ago

A geometry problem by Worranat Pakornrat

The answer is 13.

2 solutions

Moderator note:

0 pending reports