Pull Your Fair Share
The center of a solid sphere of radius R is located a distance of 2 R from a point-particle.
Approximately what percentage of the gravitational force felt by the point-particle is due to the blue half of the sphere?
Note:
There is no ambient gravitational field.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Hi, i found the centre of mass of each semisphere at a distance of 3R/8 from the middle of the sphere and assumed that the centre of mass of each semisphere would be the point mass that exerts a gravitational force and found an answer 68.1% which is quite close to the value here.could you tell me where i went wrong? Couldnt really understand your solution its too complicated for me.thanks
Log in to reply
You can only assume that the gravitational attraction is as if from a point source, except as a good approximation at large distances, if the mass distribution is spherically symmetric. The whole sphere has this symmetry, of course, but neither of the two hemispheres do, so you cannot use the point source simplification for either of them.
Log in to reply
We can. Then tell me how to find centre of mass of discrete bodies
Log in to reply
@Roy Satyam – See my comment on Peter MacGregor's post, which works a simpler case, showing that we cannot treat a uniform disc as a point particle.
I don't understand why point source simplification can't be used... I am trying to solve the problem by using the centre of mass of the blue hemisphere at a distance (2R-3R/8) and mass M/2
Log in to reply
Since the hemispheres are not spherically symmetric, we cannot simply treat them as point particles. See my comment on Peter MacGregor's post, which works a simpler case, showing that we cannot treat a uniform disc as a point particle.
Force due to blue hemisphere, F1 = Gm (M/2)/(2R-3R/8)^2 Force due to whole sphere F2 = GmM/(2R)^2 Percentage = F1 * 100/F2 Is this not correct?
Log in to reply
Since the hemispheres are not spherically symmetric, we cannot simply treat them as point particles. See my comment on Peter MacGregor's post, which works a simpler case, showing that we cannot treat a uniform disc as a point particle.
Think about Gauss theorem for electrical charges, gravitation is similar , the total flux crossing closed surface, like a sphere, wherein the charges are enclosed is constant an equivalent to the sum of all charges inside, but it does not mean that flux per square foot at any place of the surface be uniform and on whole surface. However If distance of test charge is far away you can consider it in its center of gravity as you have assumed and avoid the almost allway nasty integral that use to appear. Notice the difference by your calculation and the exact one will amount around 8% of total, the farther you locate the test charge the smaller will amount the difference. Unfortunately our problem not allows us take that path but it does an idea of magnitude of the result.
The integral can be done analytically. When done, the ratio is found to be 2 1 ( 1 7 − 7 5 ) ≈ 0 . 6 7 4 . I found that a spherical coordinate system set up at the origin of the full sphere, with its polar axis directed toward the point mass provided a nice simplification that eliminated the azimuthal dependence right away, as it must.
G m ρ R ∫ 0 1 d r ∫ 0 2 π d θ ∫ 0 2 π d ϕ ( 4 − 4 r cos θ + r 2 ) 2 3 r 2 sin θ ( 2 − r cos θ )
Log in to reply
Indeed. This is a much better use of polar coordinates.
I also came to this step but was stuck by this integral, which still looks forbidding with its denominator. Could you please give me some hint how to do it analytically?
Log in to reply
The integral with respect to ϕ is trivial.
The integral with with respect to θ is now possible (it is a function of cos θ times sin θ , so easy).
After that, we have a relatively straightforward integral with respect to r . ...
Log in to reply
@Mark Hennings – I had difficulty by doing the integral with respect to θ, but now worked it out. Thanks a lot!
How do you derive this integral? I can see that you're integrating for gravitational attraction across every point on the sphere, but since gravitational attraction depends on mass, and the equation inside the integral is for an infinitesimal point, where does mass come into the equation?
Log in to reply
The mass appears as the density ρ times the infinitesimal volume element R 3 r 2 sin θ d r d θ d ϕ .
Log in to reply
Ah, I think I see. So, for reference, I'll have to turn Gm1m2/r^2 into an integration that finds m1 and r^2 based on where you are in the sphere? Is it as simple as that or am I missing a step?
Log in to reply
@Jonathan Spirit – Exactly so. Basically, you regard the hemisphere as if it were made up of a very large number of extremely small pieces, and add up the gravitational attraction from each piece. Letting the piece size tend to zero turns the sum into an integral.
Log in to reply
@Mark Hennings – I understand. But where did (2 - r sin theta cos phi) come from? Does it result when I look for the radius?
And is R^3 strictly necessary? I searched about the volume element but none of them contained R^3.
Log in to reply
@Jonathan Spirit – x = r sin θ cos ϕ y = r sin θ sin ϕ z = r cos θ Source This integration is using spherical coordinate system. It is easier to understand the solution if you know what it is. You can find it here
@Jonathan Spirit – I used R r , for 0 ≤ r ≤ 1 to parametrize the radial coordinate for the sphere of radius R . The volume element is then ( R r ) 2 sin θ R d r d θ d ϕ = R 3 r 2 sin θ d r d θ d ϕ If am looking for the axial component of the gravitational force, and so the integral is ∭ R 2 ( 4 − 4 r sin θ cos ϕ + r 2 ) G m ρ R 3 r 2 sin θ d r d θ d ϕ × 4 − 4 r sin θ cos ϕ + r 2 2 − r sin θ cos ϕ where the last term is the cosine of the angle between the axis and the vector from the infinitesimal mass element to the mass m .
Log in to reply
@Mark Hennings – Should there be a r in − 2 sin θ cos ϕ and − 4 sin θ cos ϕ ?
Log in to reply
@Rui Xin – "Not quite" and "yes". I have corrected both. Comparing my latest post with the original makes what I intended clear...
I used the same method as Sunny Chaturvedi (Nov 30), applying the inverse square law to the centres of gravity of the two hemispheres 3/8 R from the centre of the sphere. This gives a similar result of 68.113%, but i’m puzzled by the relatively high difference between this and the method above.
Applying Newton’s Law of Gravitation: G,m,and M are common, so the two components of the attraction are proportional to the inverse squares of the distances between the two centres of mass and the particle.
Since the centre of mass of a hemisphere is 3/8 R from the centre of the base, the distances of the centres of mass from the particle are 13/8 R and 19/8 R (2 R plus and minus 3/8 R).
The contribution of the blue hemisphere is simply 19 squared (361) over the sum of 19 squared plus 13 squared (169):
361/530 = 68.1132075471698... %
I’d appreciate if someone could explain the discrepancy — is the method flawed (if so, how?) and gives a similar result by coincidence?
Log in to reply
Look at the many comments after Peter’s solution and elsewhere. You cannot simply treat the hemispheres as point particles at their centres of gravity, since they are not spherically symmetric.
Log in to reply
Oops! Thank you very much for taking the time to respond, and sorry for asking something that has already been covered. Best wishes
This solution will use methods similar to those used to derive the shell theorems. G and m will not be omitted, and the overall sign will also be omitted since they don't affect the answer (can adjust at the end). First, the potential for the blue region will be dealt with first. Since potential is not a vector, it will be easier to deal with since the potentials can all be added together, whereas integrating the force would require dealing with components.
First we find the potential a disk of density
σ
∫
0
R
′
r
2
+
y
2
2
π
σ
y
d
y
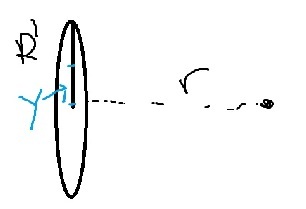 The general problem is 3-d dimensional, so later it will turn out that
σ
=
ρ
dx where x is the distance of the center of the disk away from the point mass. Evaluating the integral yields
2
π
σ
(
R
′
2
+
r
2
−
r
)
Now the potential for a thin disk of the sphere yields
d
V
=
2
π
(
R
2
sin
2
(
θ
)
+
x
2
−
x
)
ρ
d
x
The general problem is 3-d dimensional, so later it will turn out that
σ
=
ρ
dx where x is the distance of the center of the disk away from the point mass. Evaluating the integral yields
2
π
σ
(
R
′
2
+
r
2
−
r
)
Now the potential for a thin disk of the sphere yields
d
V
=
2
π
(
R
2
sin
2
(
θ
)
+
x
2
−
x
)
ρ
d
x
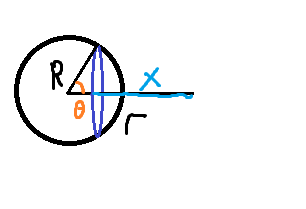 Drawing a right triangle and knowing that cos(
θ
=(r-x)/R, sin(
θ
) can be calculated. Also I'm going to get rid of
ρ
to be lazy. Plugging in the value for sin(
θ
):
d
V
=
2
π
(
(
R
2
−
r
2
−
x
2
+
2
r
x
)
+
x
2
−
x
)
d
x
=
2
π
(
2
r
x
+
R
2
−
r
2
−
x
)
d
x
Now integrating it from r-R to r: (You can verify that integrating from r-R to r+R yields 4
π
ρ
R^3/(3r) which is M/r, and U=-GMm/r.) We will be evaluating things about the blue half of the sphere for most of the problem.
V
=
∫
r
−
R
r
2
π
(
2
r
x
+
R
2
−
r
2
−
x
)
d
x
Using u-sub for u=2rx+r^2-r^2, du=2rdx for the first part, and some more work, the integral becomes
3
r
2
π
(
2
r
x
+
R
2
−
r
2
)
2
3
−
π
x
2
∣
r
−
R
r
3
r
2
π
(
r
2
+
R
2
)
2
3
−
π
r
2
−
3
r
2
π
(
2
r
2
−
2
R
r
+
R
2
−
r
2
)
2
3
+
π
(
r
−
R
)
2
Note how it's r-R instead of R-r, since raising something squared then taking the square root makes it positive. We know r>R, so we leave it as r-R.
3
r
2
π
(
(
r
2
+
R
2
)
2
3
−
(
r
−
R
)
3
)
−
π
(
2
R
r
−
R
2
)
Now we need to find the force. By definition of potential energy, we can find it by differentiating the above by r. There may be errors with the overall sign, but again that will be adjusted at the end. (F=-dV/dr, not +dV/dr. The order of integration above may also affect the overall sign, but whatever).
Pretty messy quotient rule:
3
2
π
r
2
2
3
(
r
2
+
R
2
)
1
/
2
⋅
2
r
2
−
(
r
2
+
R
2
)
2
3
−
3
(
r
−
R
)
2
r
+
(
r
−
R
)
3
−
2
π
R
After a bit of simplifying we end up with a not particularly nice equation.
2
π
r
2
r
2
r
2
+
R
2
−
3
1
(
r
2
+
R
2
)
2
3
−
(
r
−
R
)
2
r
+
3
1
(
r
−
R
)
3
−
R
r
2
Finally we plug in the situation given in the problem r=2R. After some simplifying, it ends up as
2
π
R
3
(
5
−
1
2
5
5
−
2
1
+
1
2
1
−
1
)
This, multiplied by density and G will be the gravitational acceleration at that point particle. For the entire sphere, the force (excluding density, G, and m)
3
4
π
r
2
R
3
=
3
π
R
Finally finding the ratio
3
π
R
2
π
R
(
5
−
1
2
5
5
−
2
1
+
1
2
1
−
1
)
And getting (sign got flipped)
−
6
(
5
−
2
3
−
1
2
5
5
−
1
)
=
2
1
7
−
7
5
≈
6
7
.
3
7
6
2
%
Drawing a right triangle and knowing that cos(
θ
=(r-x)/R, sin(
θ
) can be calculated. Also I'm going to get rid of
ρ
to be lazy. Plugging in the value for sin(
θ
):
d
V
=
2
π
(
(
R
2
−
r
2
−
x
2
+
2
r
x
)
+
x
2
−
x
)
d
x
=
2
π
(
2
r
x
+
R
2
−
r
2
−
x
)
d
x
Now integrating it from r-R to r: (You can verify that integrating from r-R to r+R yields 4
π
ρ
R^3/(3r) which is M/r, and U=-GMm/r.) We will be evaluating things about the blue half of the sphere for most of the problem.
V
=
∫
r
−
R
r
2
π
(
2
r
x
+
R
2
−
r
2
−
x
)
d
x
Using u-sub for u=2rx+r^2-r^2, du=2rdx for the first part, and some more work, the integral becomes
3
r
2
π
(
2
r
x
+
R
2
−
r
2
)
2
3
−
π
x
2
∣
r
−
R
r
3
r
2
π
(
r
2
+
R
2
)
2
3
−
π
r
2
−
3
r
2
π
(
2
r
2
−
2
R
r
+
R
2
−
r
2
)
2
3
+
π
(
r
−
R
)
2
Note how it's r-R instead of R-r, since raising something squared then taking the square root makes it positive. We know r>R, so we leave it as r-R.
3
r
2
π
(
(
r
2
+
R
2
)
2
3
−
(
r
−
R
)
3
)
−
π
(
2
R
r
−
R
2
)
Now we need to find the force. By definition of potential energy, we can find it by differentiating the above by r. There may be errors with the overall sign, but again that will be adjusted at the end. (F=-dV/dr, not +dV/dr. The order of integration above may also affect the overall sign, but whatever).
Pretty messy quotient rule:
3
2
π
r
2
2
3
(
r
2
+
R
2
)
1
/
2
⋅
2
r
2
−
(
r
2
+
R
2
)
2
3
−
3
(
r
−
R
)
2
r
+
(
r
−
R
)
3
−
2
π
R
After a bit of simplifying we end up with a not particularly nice equation.
2
π
r
2
r
2
r
2
+
R
2
−
3
1
(
r
2
+
R
2
)
2
3
−
(
r
−
R
)
2
r
+
3
1
(
r
−
R
)
3
−
R
r
2
Finally we plug in the situation given in the problem r=2R. After some simplifying, it ends up as
2
π
R
3
(
5
−
1
2
5
5
−
2
1
+
1
2
1
−
1
)
This, multiplied by density and G will be the gravitational acceleration at that point particle. For the entire sphere, the force (excluding density, G, and m)
3
4
π
r
2
R
3
=
3
π
R
Finally finding the ratio
3
π
R
2
π
R
(
5
−
1
2
5
5
−
2
1
+
1
2
1
−
1
)
And getting (sign got flipped)
−
6
(
5
−
2
3
−
1
2
5
5
−
1
)
=
2
1
7
−
7
5
≈
6
7
.
3
7
6
2
%
Nice solution using gravitational potentials. You have explained your reasoning in each step, this helped me understand this solution better. Thanks Sean!
Relevant wiki: Gravitation
Here is an analysis which gives an *approximate * answer to the problem.
Since we are looking for a ratio we can cut ourselves some slack, take R = 1 and ignore π , G, ρ and other numerical factors!
Measure x downwards from the red point, towards the centre of the sphere. Slice the sphere up like an onion, with the layers perpendicular to the x-axis. Now we have a stack of disks with their centres of gravity on the x axis, their distance from the red point being x , and their area being proportional to the square of their radius. By an easy application of Pythagoras this is 1 2 − ( 2 − x ) 2 = 4 x − 3 − x 2 . Now we imagine that all the mass of each disk of thickness d x is concentrated at its centre (see note).
Using the inverse square law for gravity, we can sum the effects of the disks by integration to find our ratio -
∫ 1 3 x 2 4 x − 3 − x 2 d x ∫ 1 2 x 2 4 x − 3 − x 2 d x = lo g 8 1 − 4 lo g 1 6 − 2 5 = 0 . 6 9 1 1 = 6 9 . 1 1 %
note.
The gravitational field of the disk and an equally massive point at its centre of gravity are only approximately the same (see Mark Henning's comment below). Treating them as equal is what turns this solution from an exact analysis into an approximation. The further the red point is from the sphere, the better this approximation becomes. I'm surprised to be within 5% of the correct answer when the point is only 2 R from the centre of the sphere!
This problem made me realize something I've heard many times but never really understood the significance of: a sphere of constant density can be replaced with a point mass at its centre of mass. So any distribution of mass that is not spherically symmetric (e.g. the discs you integrate over) will exert a force that is strictly smaller than what the same mass arranged in a symmetric way would do.
Can someone explain why the following thinking is incorrect: The centre of mass of a hemisphere is 3/8's 'the way up' from the base So the blue hemisphere's force on the point is FB = (GM)/(13R/8)^2 While the whole sphere force of FS = (GM)/(2R)^2 And therefore the amount excerted by blue hemisphere is FB/FS ~ 75.7%
Log in to reply
Me as well
Same.Wonder what went wrong.
You cannot model the hemisphere as a point particle, since the hemisphere is not spherically symmetric. As I showed above, it is not possible to take an object which is not spherically symmetric and model it is a point particle, except as a (good) approximation at large distances.
Log in to reply
Wow! I can't believe I've never though of this before! Now it seems obvious. A large hollow ring (radius R) would have center of mass at the geometric center of the ring, but the actual gravitational force acting on a point particle near (<<R) that center of mass would in fact be a lot weaker than G m1 m2/(distance to center of mass)^2 since the distance to the actual mass on the outer ring would be far greater than the distance to the center of mass. Thank you! It's just so damn tempting when a problem seems to have a simple answer...
I approximated the force due to the two hemispheres separately, and it led to me guessing the correct answer. Here was my thought process:
F_blue ~ (2-3/8)^-2
F_green ~ (2+3/8)^-2
pct blue = F blue/(F blue+F green) = 68.1%
Maybe the error partially cancels this way?
You are assuming that a uniform circular disc of mass m and radius a exerts a force of R 2 G M m on a mass M a distance R from the centre of the disc on the axis of that disc. In other words, you are assuming that you can treat the disc as a point mass. You cannot.
Splitting the disc up into circular sections (all parts of which are the same distance from the point mass, and subtend the same angle with the axis of the disc), the actual force is along the axis, and of magnitude ∫ 0 a π a 2 G M 2 π x d x × R 2 + x 2 1 × R 2 + x 2 R = a 2 2 G M m R ∫ 0 a ( x 2 + R 2 ) 2 3 x d x = a 2 2 G M m R [ R 1 − R 2 + a 2 1 ] which is approximately equal to R 2 G M m when R ≫ a .
Since the disc is not spherically symmetric, treating it as a point mass is only an approximation. The same applied to the whole hemisphere.
Log in to reply
What do you mean by "not spherically symmetric"? Is the point mass 'm' not on the perpendicular axis of the imaginary plane separating blue hemisphere and green hemisphere?
Log in to reply
The disc is not sphere-shaped! As I have shown here, you cannot replace the disc by a point mass at its centre.
Thanks Mark.
I'm kicking myself for falling into this error, and have modified my solution appropriately.
Well this is an approximate method just like that of Peter Macgregor's, the correct solution is already provided by Mark Hennings.
Let's cut the sphere in two parts and let the whole mass of each sphere (i.e. M/2) be concentrated at its centre of mass i.e. 3R/8 from base, now you have three point size particles, and gravitational field could be easily calculated and the ratio of required quantity comes out to be 68.11% (that's damn close)
Caution-this was just a quick objective approach, in practise we can never change the mass distribution in space to calculate field, it alters the field at every point.
:)
I did a numerical simulation in a spreadsheet (one of my favorite methods).
I created a semicircle in a 10 by 20 array, labeled .05 to .95 along the short X axis and -.95 to .95 along the longer Y axis (steps of .10 in both directions). Within the semicircle, each cell represents an annulus of mass within the sphere. The gravitational effect of each annulus is proportional to the mass, which is proportional to the radius of the annulus, thus the X label of the cell.it is inversely proportional to the distance from the cell's (X,Y) label to the point (0,2). This is then adjusted by the cosine of the angle between the center line and the line between (X,Y) and (0,2), to eliminate the outward direction of the gravity.
Summing over the 2 halves of the semicircle yields 5.480902 for blue and 11.340153 for green, with a ratio of 67.4164%.
Using Cartesian coordinates, otherwise similar to Mark Hennings' solution.
Assuming [ − 1 ≤ x ≤ 1 ∧ − 1 ≤ y ≤ 1 ∧ − 1 ≤ z ≤ 1 , ∫ 0 1 ( ∫ − 1 − x 2 1 − x 2 ( ∫ − − x 2 − y 2 + 1 − x 2 − y 2 + 1 ( ( 2 − x ) 2 + y 2 + z 2 ) 3 / 2 2 − x d z ) d y ) d x ] ⇒ − 6 1 ( 7 5 − 1 7 ) π
Assuming [ − 1 ≤ x ≤ 1 ∧ − 1 ≤ y ≤ 1 ∧ − 1 ≤ z ≤ 1 , ∫ − 1 1 ( ∫ − 1 − x 2 1 − x 2 ( ∫ − − x 2 − y 2 + 1 − x 2 − y 2 + 1 ( ( 2 − x ) 2 + y 2 + z 2 ) 3 / 2 2 − x d z ) d y ) d x ] ⇒ 3 π
− 3 6 π ( 7 5 − 1 7 ) π ⇒ 2 1 ( 1 7 − 7 5 ) ≈ 0 . 6 7 3 7 6 2 0 7 8 7 5 0 7 3 6
Relevant wiki: Gravitation
If the density of the sphere is ρ , using polar coordinates we can write the attractive force from the blue hemisphere as G m ρ R ∫ 0 1 d r ∫ 0 π d θ ∫ − 2 1 π 2 1 π d ϕ ( 4 − 4 r sin θ cos ϕ + r 2 ) 2 3 r 2 sin θ ( 2 − r sin θ cos ϕ ) while the total attractive force from the whole sphere is G m ρ × 3 4 π R 3 ( 2 R ) − 2 = 3 1 π G m ρ R which is of course the same as we obtain from the above integral, replacing the ϕ limits by − π and π .
Evaluating this multiple integral numerically, we see that the blue sphere is responsible for 6 7 . 3 7 6 % of the total gravitational attraction.