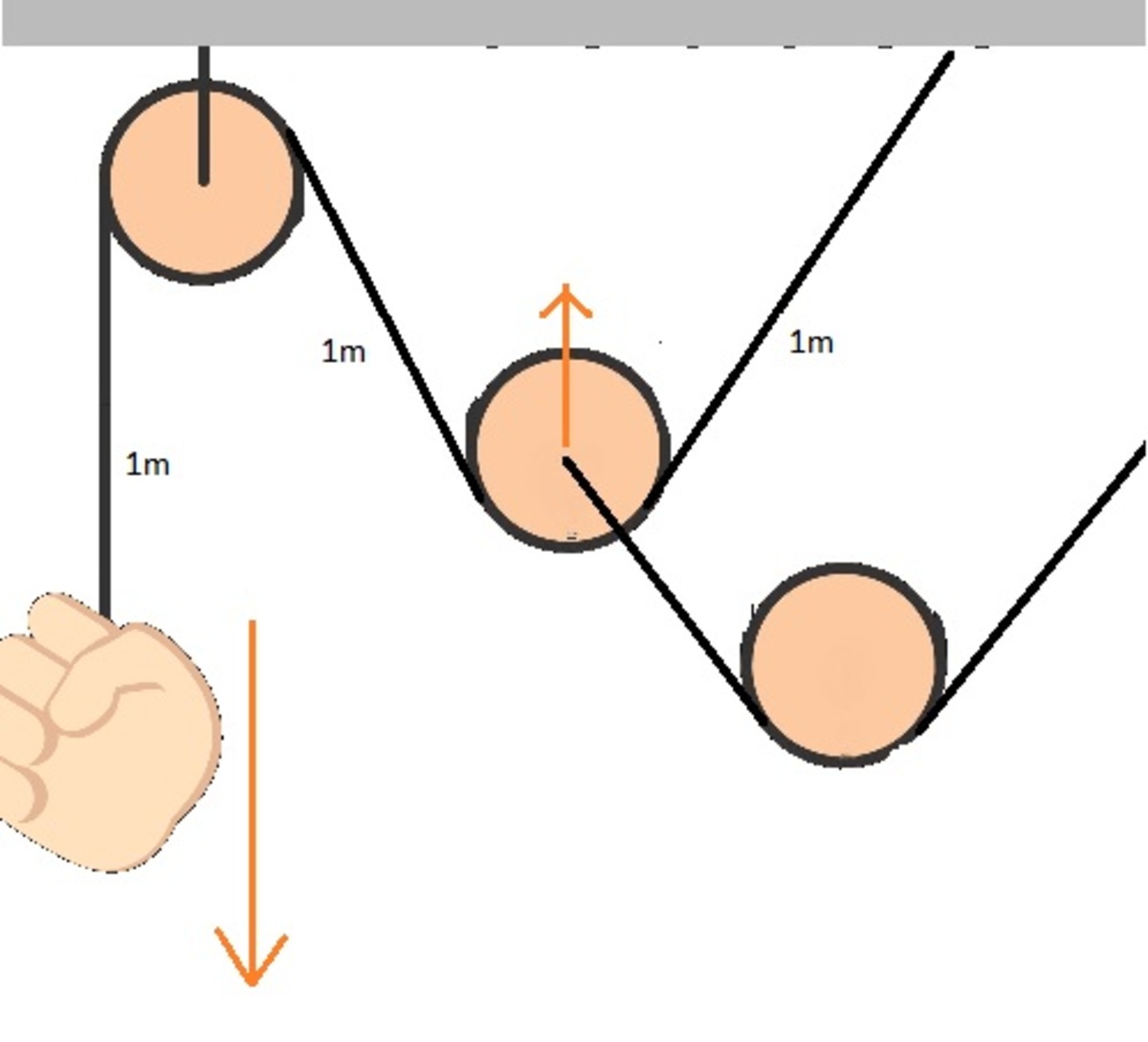
Pulley System
Note
: the rope lengths are
NOT
drawn to scale.
How far (in meters) should the hand pull the rope to move the pencil from A to B ?
Assume that the hand pulls the rope straight down and that the pulleys are far enough apart that they do not collide with each other.
The answer is 64.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
The problem itself needs to be better explained. I understand one needs to know about pulleys but the picture in the original problem is misleading.
Log in to reply
I totally agree : didn't know what to do with the picture myself.
Log in to reply
It’s an interesting puzzle but even the clip you included with your solution might have helped get some information.
I don't know why is that! I think the drawing is clear and no need for more explanation. More explanation mean solving the problem, need a pit effort to think how to solve it and it is not a complecated system!
Log in to reply
I solved it assuming the rope connecting the first with the second pulley has a length of infinity, and each pulley connected to the previous one(not connected to the previous rope) starting from the 3rd left to right. I think the figure should show that to make it clear.
Log in to reply
@Mehdi K. – The picture in my solution is a part of the original picture that I attached to the problem, it's clearly shows that the rope connected to the pulley not the the other rope. Brilliant staff did modified the picture (they put the 1 m between A and B) as I wasn't showing that in the picture but I did mention in the comments. I don't know if the original picture still not clear to you!
Yeah, I was confused too. A brief description of how the pulleys were arranged would have added much needed context.
I do not think this is the correct solution. The problem asked for the distance that the hand needs to travel to move the pencil 1 meter. If 1 meter of rope was pulled from the pulley, then 1 meter would also be pulled into it on the other end, resulting in the pulley moving 1 meter. Since the load pulley has to move one meter of rope to move the pencil the acquired distance, its loading pulley also needs to move up one meter. This will result in a chain that will has each pulley using one meter of rope.
Moving along to the working end of the system, the second-to-last pulley will need to move up 1 meter. To do that, the hand will have to pull on 2 meters of rope: 1 from the rope connected between the ceiling and the pulley, and 1 between the last two pulleys. The last pulley will not affect this length, since it will not change position as the pulley is directly latched onto the ceiling, and the working rope that is being used above it to pull the pencil and contributing to the system will only push down on it, instead of being pushed toward the ceiling. Therefore, I conclude that only 2 meters of rope will need to be pulled by hand in order for the pencil to move up 1 meter.
Log in to reply
the normal pulley mechanics don't apply as each pulley is attached to the ceiling, so its only 2 meters
The design of this pulley system would not allow the hand to move the pencil at all.
Log in to reply
the drawing is not to scale. The assumption should have been clearer: Assume that the hand pulls the rope straight down and that the pulleys are far enough apart that they do not collide with each other nor the ceiling.
Can you please elaborate your solution. Why is a pull of 2m required for each pulley to move 1m? Why is the tension required for a pulley multiplied by the tension required for the previous pulley? I know I'm wrong but shouldn't a pull of 1m be enough as the pull would be carried on to each successive pulley and finally to the pencil.
I found the diagram confusing. The way it is drawn I couldn't tell what rope went where or see how the pulleys are connected or how they work together.
The drawing is bad, that's not how rope would go through the pulleys.
Geez, guys, lighten up a bit.
The picture shows that for the pulley to move up 1 m,
each
of the two ropes supporting it must move 1m. Which means 2m of rope must be pulled.
The rope lengths aren't drawn to scale as it says. That's the first misleading part. 64 m is much too long in the picture. The picture the way it is drawn shows the pulleys are connected uniformly. It almost looks not possible as drawn. Once you tug there is an extra meter in which it pulls before pulling the other pulleys. The pulleys in between look irrelevant to the problem other than adding length. It looks to me that 2 m is enough. If you take the radius of each pulley looks about 0.5 m. That gives a diameter of 1m. Count the number of pulleys that would fit between. 8 pulleys a little bigger than 1m in diameter and a fraction of a meter apart. More than 8 meters to begin with. At 2 m for every tug, you're looking at 64 m
The condition that "For each moving pulley it is require to pull 2 m of rope to move the pulley one meter" is applicable only if we are given the explicit information that the ropes are all exactly at 90 degrees. And also that the wheels themselves are negligible in circumference, else the solution does not hold. For example, in the original diagram, imagine that the second-from-left wheel is supported by ropes that are at 45 degrees on either side. Your solution will fail. Interesting question, but needs more detail for an accurate solution.
Uh, you'd need more rope than the diagram allows. Problem unsolvable under realistic conditions with the literal diagram. The rope being pulled stops being able to be pulled any further after at most a few meters.
Better to Go from B to A, no more rope needed and Go faster, thanks to the Apple tree and take care of tour Head! ;)
@Ahmed Almubarak Why is relation geometric 2 4 8 15... not arithmetic 2 4 6 8....
Ok. Let's try this. Forget about the diagram and simplify. Let's say we have one pulley with a rope around it.
This rope goes down 1 meter and then you have the pulley and finally goes back up one meter for a total on 2 meters. The pulley always rests in the middle, in this case one meter down.
Now, pull up one side one meter so that you have only one meter around the rope. The pulley will rest in the middle and that's half a meter.
From the previous set up I think I can generalize and say that for every distance D I pull up, the pulley will go up half D.
Now let's see the last pulley (7). This pulley does not move so the translation on the rope on the left side of it is the same as the translation on the right side of it and from my previous point if the hand pulls down a distance D then pulley (6) will go up half D.
Finally, if you want the first pulley to go up one meter then the second one will have to go up 2 meters, the third one 4, the fourth 8 the fifth one 16, the Sixth one 32 and the hand 64.
Exactly! It's clear that this is a problem ennounced in ideal conditions, so every pulley doubles the amount needed to pull.
There are 7 pulleys, only 6 of which do any distance changing since the leftmost simply redirects the pull. Pulleys have rotational symmetry so any translational movement be it the center or the outskirts will differ by a constant, C. Thus far, the rope will need to be pulled A*C^6, A being the starting length (that is, A will be scaled by C, 6 times). C is 2 because there are two circumferential points that transverse with the center of the pulley.
The diagram isn't representing a meaningful pulley system. All that is shown in the diagram is a rope looped around some wheels. It wouldn't accomplish anything. Read this http://www.explainthatstuff.com/pulleys.html Pulley systems have several loops of rope holding up the same mass, thus spreading out the force - so th effort you have to put in is reduced. In any case, the multiplier of a pulley system isn't an exponential, it's just a multiplier. Four ropes = 1/4 th force, 4x the distance. Simple. Because work done = force X distance moved.
The premise that "for the pencil to move up 1m, the previous pulley must be pulled up 2m, and the one before it by 4m and so and so forth till you get the answer as 64", is applicable only if we are given the explicit information that the ropes are all exactly at 90 degrees. And also that the wheels themselves are negligible in circumference, else the solution does not hold. For example, in the original diagram, imagine that all the wheels are supported by ropes that are at 45 degrees on either side. For convenience I have marked 1m lengths on the picture. Now when the left most rope is pulled down 1m, the second wheel will not be shifted up by 0.5m. If the ropes were 90 degrees, then yes, the second wheel would have moved by 0.5m.
Interesting question, but needs more detail for an accurate solution.
The only thing they explicitly mentioned as not being to scale were the rope lengths.
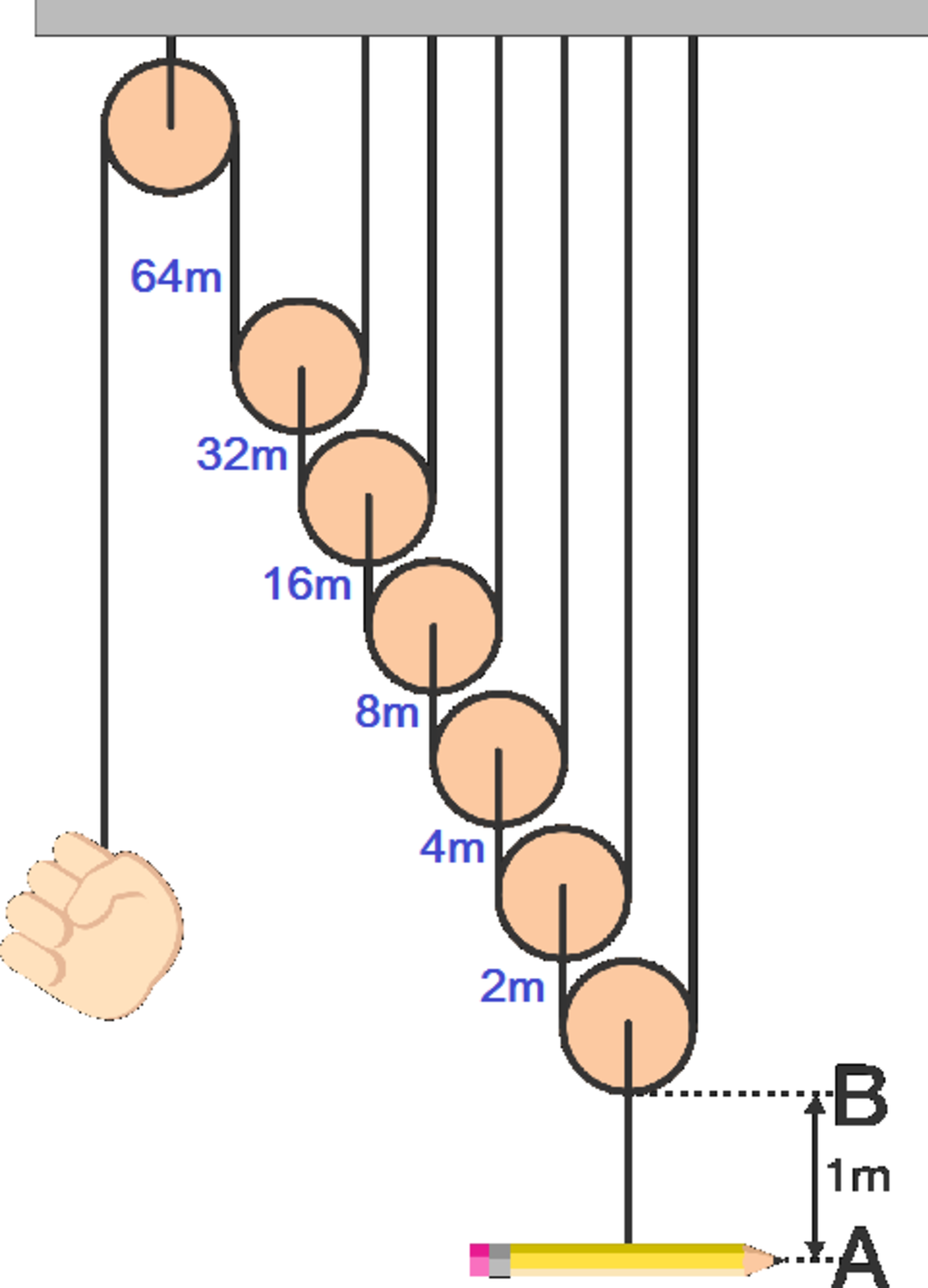
For each pulley to raise 1 m of height, we need to pull 2 m of rope. Since there are 6 movable pulleys we need to pull 2 6 = 6 4 m of rope.
Watch this 3min video on how pulleys work
For each pulley that isn't fixed, the mechanical advantage is such that the hand pulls with half as much force. There are 6 non-fixed pulleys, so the force required to lift the pencil is (1/2)^6 = (1/64) the weight of the pencil.
In order for energy to be conserved, the work done by the hand will equal the work done to the pencil.
Work by hand = (1/64 weight of pencil) * (length of rope pulled)
Work done to pencil = (weight of pencil) * (1 meter)
Set these quantities equal and solve for the length of rope: (1/64) L = 1 m -> L = 64 m
For each moving pulley it is require to pull 2 m of rope to move the pulley one meter. see below picture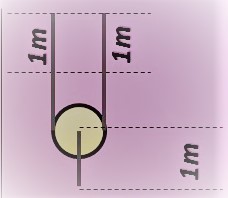 So first rope will move 2 m, second will move 4 m, third 8 ... rope 6
2
6
=
6
4
m
So first rope will move 2 m, second will move 4 m, third 8 ... rope 6
2
6
=
6
4
m