Pulleys and strings

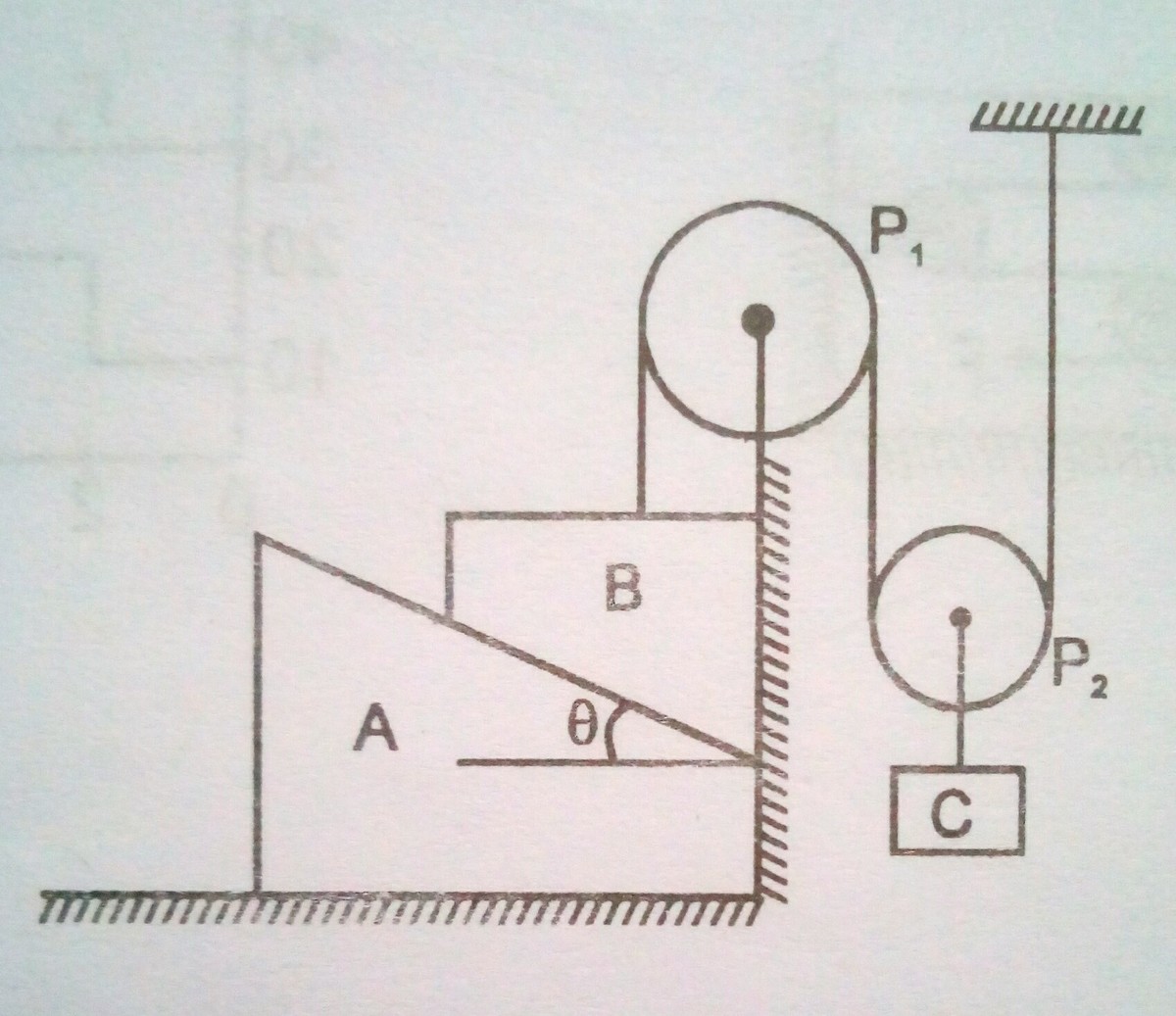
In the above figure, $P_{1}$ and $P_{2}$ are massless pulleys, $P_{1}$ is fixed and $P_{2}$ can move. Masses $A,B$ and $C$ are $\dfrac{9m}{64},2m$ and $m$ respectively. All surfaces are smooth and the string is massless. If it is given that $\theta=\tan^{-1}\left(\dfrac{3}{4}\right)$ , find the magnitude of acceleration of block $C$ in $\text{ms}^{-2}$ .