Pulleys Pulleys Everywhere -3
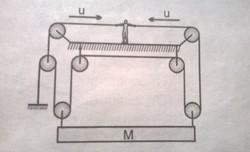 System is shown in the figure and man is pulling the rope form both sides with constant speed
. Then the speed of the block will be? (
can only move vertically)
System is shown in the figure and man is pulling the rope form both sides with constant speed
. Then the speed of the block will be? (
can only move vertically)
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Imagine blocks A and B being pulled at the speed of u instead of man pulling the string at speed u .
By the concept of virtual-work method ∑ T . V = 0
Let the velocity of mass M be v in upward direction. Applying "T.V" we get
− T u − 2 T u + 2 T v = 0
So v = 4 3 u .