Pulleys to the Rescue

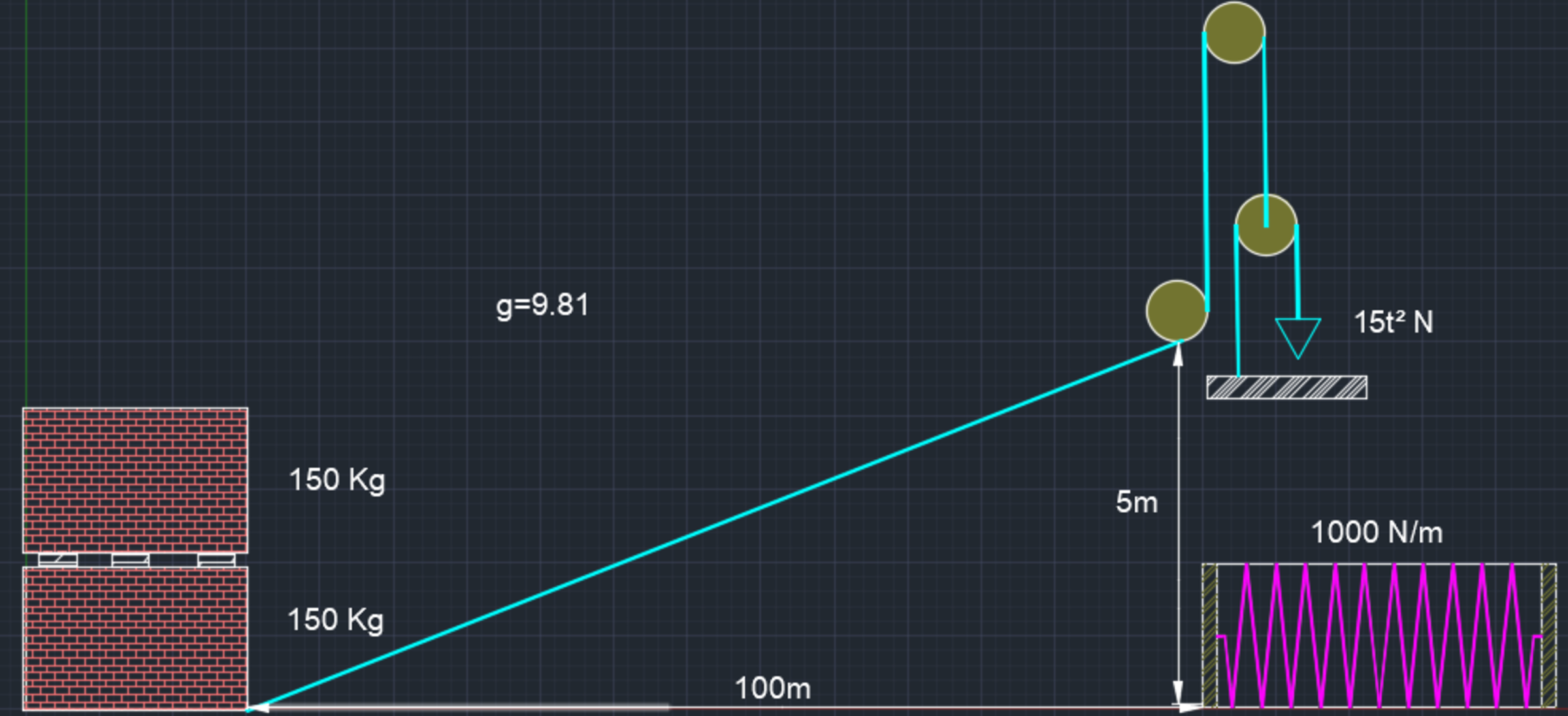Classical Mechanics Level pending

Workers at a brick manufacturing plant are behind schedule and need to move crates of bricks quicker. They decide to stack one crate upon another and modify the motor-cable system to accommodate the additional weight. The motor can exert a maximum force of 1500 N after 10 seconds. Before t=10 seconds the motor exerts a force F(t)=15t^2 N. The motor abruptly disconnects at t=12.5 sec. They aren't sure if the crates will remain stacked under the applied force but give it a try. There is a spring with k=1000 N/m at the motor. How far from the spring will the crates come to rest if the motor runs for a full 12.5 seconds? Note: The coefficient of static friction b/t the floor and crate = o.70. The coefficient of static friction b/t the crates = 0.65. The coefficient of kinetic friction = 0.45. There is no friction beneath the spring and energy is conserved. g=9.81 m/s^2.


The answer is 1.964.

A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Steven Chase
Mar 24, 2020 
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
 
import math

# Constants

h = 5.0

m = 300.0
k = 1000.0
us = 0.7      # Assume that blocks hold together
uk = 0.45
g = 9.81

dt = 10.0**(-5.0)

print "height"
print h
print ""

####################################################################

# Determine the time at which the block starts moving
# This is when the horizontal pull exceeds .....
# ... the product of the static friction coeff and the upward normal force
# (Fx,Fy) are the pulling forces from the cable

t = 0.0

theta = math.atan(h/100.0)

Fx = 0.0
N = m*g

while Fx <= us*N:

    F = 30.0*(t**2.0)

    Fx = F*math.cos(theta)
    Fy = F*math.sin(theta)

    N = m*g - Fy

    t = t + dt

print "tstart"
print t
print ""

####################################################################

# Calculate the block motion until t = 12.5
# ...when the motor stops pulling
# x corresponds to the location of the block (treated as a point particle)

tstop = 12.5 

x = 0.0
xd = 0.0
xdd = 0.0

while t <= tstop:

    x = x + xd*dt
    xd = xd + xdd*dt

    theta = math.atan(h/(100.0-x))

    if t <= 10.0:
        F = 30.0*(t**2.0)
    else:
        F = 30.0*100.0

    Fx = F*math.cos(theta)
    Fy = F*math.sin(theta)

    N = m*g - Fy

    Fxnet = Fx - uk*N

    xdd = Fxnet/m

    t = t + dt

print "x when pull stops"
print x
print ""

####################################################################

# Calculate sliding distance after pulling stops

E = 0.5*m*(xd**2.0)

# E = uk*m*g * D

D = E / (uk*m*g)

print "dt"
print dt
print ""

# Subtract the sum of the two distances from 100

print "Final distance from spring"
print (100.0 - (x+D))



####################################################################

#height
#5.0

#tstart
#8.15051999986

#x when pull stops
#42.7723285436

#dt
#1e-05

#Final distance from spring
#1.96353475105

0 Helpful 0 Interesting 1 Brilliant 0 Confused

You've sold me on you're iterative approach to problem solving. It makes things so much easier than fussing around with complicated integrals or equations. By the way, since I have all this time on my hands, I revisited that FEM program with a mass hanging from two springs. Made both k's equal and found the answer using minimum energy. When I ran same problem in FEM, got a completely diff. answer again. Turns out, even when the program models springs, it 1st determines forces from initial geometry and holds them constant throughout deflection. For stiff members I can see this is valid, but not for springs. Anyway, hope your doing well. Happy problem solving!

A Former Brilliant Member - 1 year, 2 months ago

Log in to reply

Thanks. Yes, I like that I can do things in baby steps, without having to deal with big expressions. That's an interesting note about the FEM program only being applicable to semi-rigid beams. It looks like you are using Mathcad. I also use Mathcad a bit, but not for dynamics problems.

Steven Chase - 1 year, 2 months ago

Log in to reply

Agreed, I can see your point. I like Mathcad - alot - but I've found you really have to be careful when solving complicated problems. I've gotten erroneous results several times. It has to do with the way Mathcad routines approximate equations. Just today I solved an integral problem. It was a level 5 deal and the integral was equated to an expression. So, I typed it in and solved for beta. But it was wrong. Then I evaluated the integral alone, and then set the expression equal to that value and got the correct answer. It seems like integrals are especially sensitive in Mathcad. I take it you're an electrical engineer based on some of your postings?

A Former Brilliant Member - 1 year, 2 months ago

Log in to reply

@A Former Brilliant Member – Yes, I'm an electrical engineer. Of course, the numerical integration techniques I use require convergence tests (running with progressively smaller time steps) to verify the quality of the result. But those checks tend to be pretty reliable, since the accumulated error (for a given time period) is a function of the time step.

Steven Chase - 1 year, 2 months ago

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...