Push Hard!
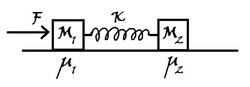 Find the
minimum
Force
F
required to move
M
2
.
Find the
minimum
Force
F
required to move
M
2
.
Details and Assumptions:
∙
M
1
=
3
K
g
∙
M
2
=
5
K
g
∙
μ
1
=
0
.
4
∙
μ
2
=
0
.
6
∙
g
=
9
.
8
m
/
s
2
The answer is 26.46.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Discussions for this problem are now closed
actually.... have you tried ... using force at some angle....... NOT JUST HORIZONTAL..... FORCE WILL BECOME EVEN LESS......
But the thing is that the one who has set this problem has shown the direction force. Otherwise u r absolutely correct..
Great idea :)
SOLUTION IS WRONG..IT SHUD BE 41.16
I think I know what you did wrong, since I did the same thing. You can't just use Newton's second law with k.x, because it is a variable force. That means, to find F you need to solve the differential equation (next solution), because you need to take into account that a also varies with time and a is the second derivative of position with regard to time.
No, it is correct. This was the objective of the problem...I knew many people were gonna get it wrong..
Why didn't we use the force equations from the FBDs?
When M1 reaches the equillibrium position where limiting friction acts on M2, M1 will have some kinetic energy... as F>μ1M1g and due to this K.E , wvwn if we remove force F, M1 will move on it's own dissipating energy in friction and spring potetnial energy.. Hence it is better to use a force such that at the equillibrium position K.E=0
can you explain me clearly why the change in kinetic energy in M1 is equal zero?
Change in K.E is zero for M2, not for M1...
It is zero for both of them (that's why the word "just moves" is used)
srry dude it is a constant force and it will create an acceleration for m1 and the spring force will try to decelerate it. but when it reaches the position at which m2 also just starts to move , the velocity of m1 is not zero. the force will be zero on that position of m1 but it will have velocity. please recheck your solution. do it using forces. :)
Zero for M 1 meaning between final and initial states because if it is zero for every elementary displacement then F has to vary accordingly.
@Sudeep Salgia – Yes, and thats why, the change in K.E is zero...thats what I said.
when u diffrentated 1/2kx2 it shud be kx not 1/2kx.plz check
I didn't differentiate, my friend...I just set
Δ
K
.
E
.
as zero, and then I
cancelled
one
x
from the equation....
I hope you understand.
excellent solution
Solution without using energy.
let x be a displacement for M 1 . Using Newton 2nd law for M 1 we get, a + M 1 k x = M 1 F − μ 1 M 1 g with initial condition x ( 0 ) = 0 and v ( 0 ) = 0 .
Those are equation for simple harmonic oscillation, then we could write the solution as x ( t ) = k F − μ 1 M 1 g ( 1 − cos ( ω t ) ) and the velocity, v ( t ) = ω k F − μ 1 M 1 g sin ( ω t )
For minimum F , the second mass will move when M 1 at maximum compression, i.e. the velocity is zero. It occurs at t = π / ω and the maximum compression is x m = 2 k F − μ 1 M 1 g .
Since M 2 just about to move, then k x m = μ 2 M 2 g , or F = 2 2 μ 1 M 1 g + μ 2 M 2 g
Hence, F = 2 6 . 4 6 N .
Yes, well done.
wat the hell!!!! u r using shm where dissipating forces r working!! XD XD lol. it could have done shm if the floor was smooth
The resultant force is constant since dissipation forces are not variable with distance or velocity in this case..hence it is justified.
Can you tell me how to write the equation x(t) from the Newton's Second Law step by step please?
force greater than U1M1g will start move first block and it would cross mean position and stop at other exreme..spring will be most compressed when this block reaches other extreme. hence second block can move with least force at this moment.. F-U1M1g = Kx, 2kx=U2M2g.. solving it we get F=26.46 N
Let M 1 be displaced by a small distance x
Using the Work energy theorem,
F x − μ 1 M 1 g x − 2 1 K x 2 = Δ K . E .
For the situation that M 2 just moves,
Δ K . E . = 0
Thus,
F − μ 1 M 1 g − 2 1 K x = 0
F = μ 1 M 1 g + 2 1 K x
For M 2 to move slightly,
μ 2 M 2 g = K x
Hence,
F = μ 1 M 1 g + 2 1 μ 2 M 2 g
F = ( μ 1 M 1 + 2 μ 2 M 2 ) g
Therefore,
F = ( 0 . 4 × 3 + 0 . 3 × 5 ) × 9 . 8 = 2 6 . 4 6 N