Pushing the boundaries
 Let circle
A
have the equation
x
2
+
(
y
−
2
)
2
=
4
and circle
B
have the equation
x
2
+
(
y
+
1
)
2
=
9
.
Let circle
A
have the equation
x
2
+
(
y
−
2
)
2
=
4
and circle
B
have the equation
x
2
+
(
y
+
1
)
2
=
9
.
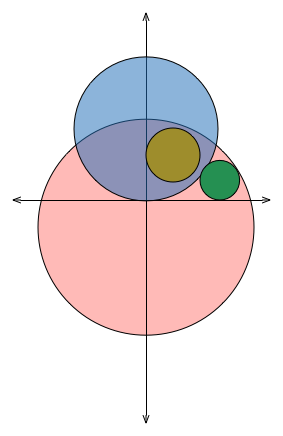
Now let C 1 be the circle in the first quadrant that is tangent to A , B and the y -axis, and C 2 be the circle in the first quadrant that is tangent to A , B and the x -axis.
If the center of C 1 is at ( x 1 , y 1 ) and the center of C 2 is at ( x 2 , y 2 ) , then find
( y 2 x 2 ) ∗ ( x 1 + 3 y 1 ) .
Clarification: To guarantee a unique solution, both C 1 and C 2 must lie inside B and must both lie entirely within the first quadrant, (inclusive of the x and y axes).
The answer is 16.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nice solution, Krishna; thanks for posting it. Just one typo, though; in your last line, it should be R X rather than X R . :)
Log in to reply
Hey! I found that there is 1 more C 2
x 2 + ( y − 1 ) 2 = 1
This is tangent to A at origin(x-axis too)
And to B at (0,2)
What do you say?
Log in to reply
Yes, that triangle would meet all the requirements, except my intent was that both C 1 and C 2 must lie entirely within the first quadrant, (inclusive of the x - and y -axes). I will add another clarification so that my intent is clear; thanks for pointing this out. :)
You have a few typos
r 2 + ( y − 2 ) 2 should be r 2 + ( 2 − y ) 2
and X 2 + ( X − 2 ) 2 should be X 2 + ( 2 − R ) 2
Why do you think the rating has been dropping?
Log in to reply
Is that a typo? They are same
Log in to reply
Oh yeah... crap... But I don't get why it is X − 2 instead of R − 2 or 2 − R for the second one
C 1 has center ( ( 1 2 3 − 2 0 ) , ( 8 − 4 3 ) ) , and C 2 has center ( 2 , 2 1 ) .
Thus ( y 2 x 2 ) ∗ ( x 1 + 3 y 1 ) = ( 2 1 2 ) ∗ ( 1 2 3 − 2 0 + 2 4 − 1 2 3 ) = 4 ∗ 4 = 1 6 .
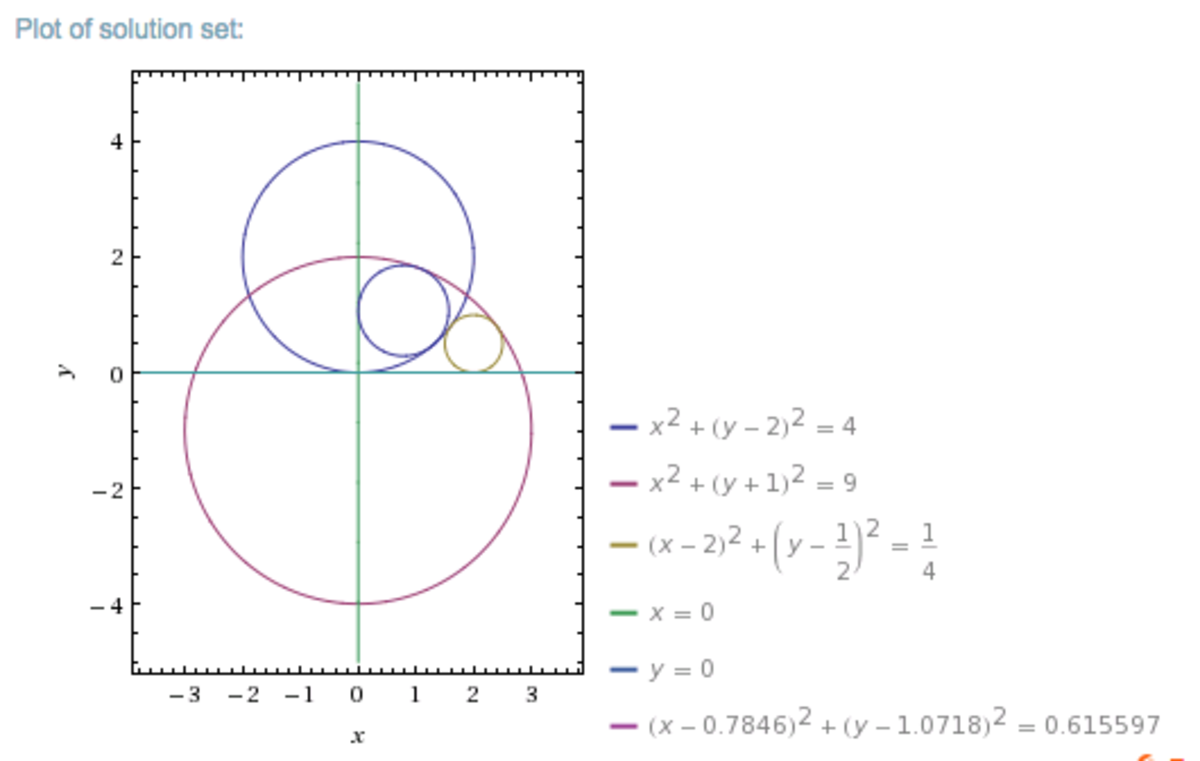
I will post the solution method shortly, but for now,
here
is a diagram of the quartet of circles.
EDIT: I apologize for "pushing the boundaries" of everyone's patience in the refinement of this question. I appreciate all your input. :)
The problem is ambiguous. The circle with equation ( x − 4 ) 2 + ( y − 2 ) 2 = 4 is also tangent to A , B , and the x -axis (and it lies in the first quadrant).
Log in to reply
@Jon Haussmann Thank you! I had a sense that there might be an ambiguity but I just wasn't seeing it; now it's so clear I wonder how I missed it. Thank you also for leaving a comment rather than reporting the question; this is why I like to get some sort of solution posted right away, (even if it's not complete), so that others can catch a mistake like this and let me know directly. Regards.
Log in to reply
No problem! Interestingly, I also had a feeling that there was another circle C 2 that satisfied the conditions, but I couldn't find it. I guess we all have our blind spots.
Log in to reply
@Jon Haussmann – Haha. Yes, I guess we do. Pranshu Gaba found yet another one, which I hope, given the amended clarification, will be the last. :)
I missed the point that the whole circle C1 had to be in the first quadrant. I thought that it was sufficient that the centre was in the first quadrant. I consequently got the center of C1 to be (38...., 14...)
Log in to reply
@Guiseppi Butel – Sorry about that. :( When I first wrote the question I had "lying entirely in the first quadrant" in the text, but then shortened it for sake of brevity before posting the question. I guess I should have left it there rather than ending up adding a clarification after the fact. It's often a challenge to avoid ambiguity when posting an original question, particularly in geometry.
Log in to reply
@Brian Charlesworth – I guess I took your title "Pushing the boundaries" too literally. My first center has humungus coordinates (in the 10th power of 10), trying to solve a triangle where the hypotenuse was 2 units greater than value for the x coordinate. After I corrected my error I still got a value greater than 30 for the x coordinate.
Log in to reply
@Guiseppi Butel – Oh wow, I didn't see that possibility at all. :)
Log in to reply
@Brian Charlesworth – I am getting a third possible circle for C 1 . Its center is ( 2 5 1 2 6 − 8 , 5 4 + 4 6 ) . It touches A internally and B externally. I think adding the condition that C 1 must also lie inside B will eliminate that case.
Log in to reply
@Pranshu Gaba – Sigh.... You're absolutely right. There are circles showing up everywhere. The added condition you have suggested should (finally) clear up any ambiguity, so thank you for that. :)
I see that you solved the question despite the ambiguity. I hope that you didn't end up wasting attempts on the other possibilities.
Log in to reply
@Brian Charlesworth – It wasn't a problem since there was only one case where the final answer was an integer. The question now looks complete to me .
Log in to reply
@Pranshu Gaba – Great. Thanks for the feedback. :)
I'm confused by your pink circle and the brown circle. I can't see their connection with the parameters supplied.
Log in to reply
The moderator put that image up without my knowledge, and I agree that it does not represent the parameters of the question. I will ask @Calvin Lin if a more representative image can be posted instead.
Log in to reply
Ooops. Is the image better now?
Log in to reply
@Calvin Lin – Perfect. Thank you!
Log in to reply
@Brian Charlesworth – Circle B is not represented, to my thinking. Its center is (0,-1) with radius 3.
Log in to reply
@Guiseppi Butel – Alright, I moved it further down so that it's better represented.
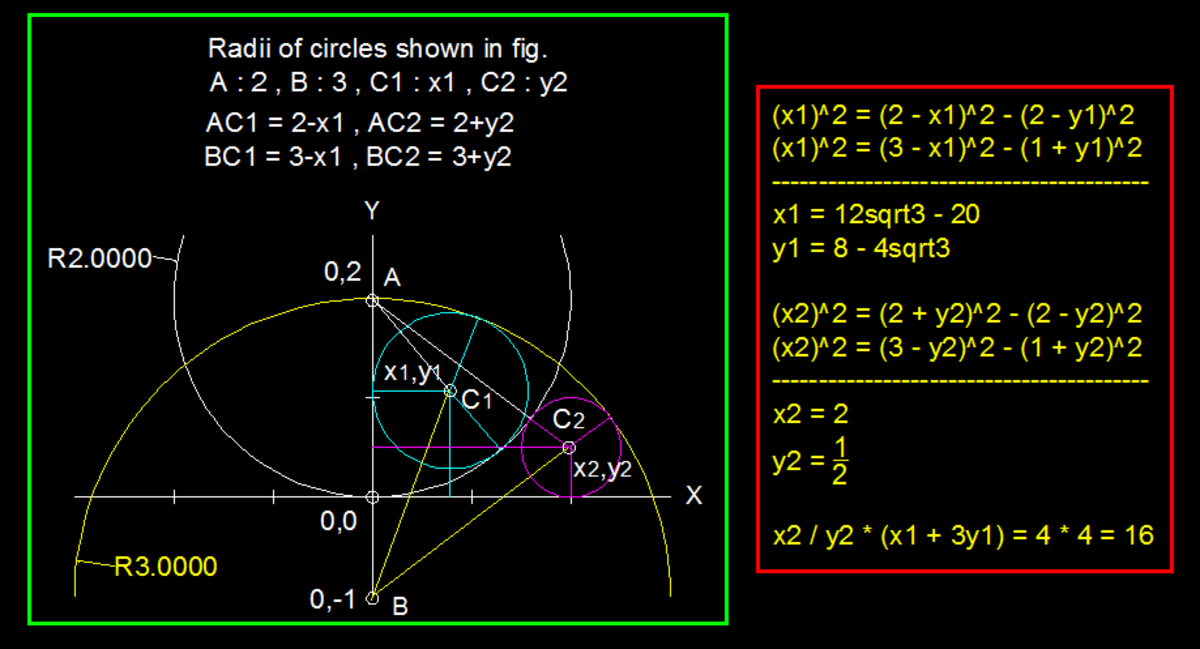
Ok so let me post the solution try to understand without diagram
Solving for C 1
Let centre be (x,y) and radius r
As C 1 touches y-axis, x-coor. of centre = r
C 1 will touch both circles internally so
Distance between centres = difference in radius
r 2 + ( y − 2 ) 2 = 2 − r
r 2 + ( y + 1 ) 2 = 3 − r
Solving these 2 equations we get
r = 1 2 3 − 2 0 , y = 8 − 4 3
r + 3y = 4
Solving for C 2
Let the centre be (X,Y) and radius 'R'
As C 2 touches x-axis, y-coor. = R
C 2 will touch the circle with centre(0,2) externally and circle with centre(0,-1) internally
X 2 + ( R − 2 ) 2 = 2 + R
X 2 + ( R + 1 ) 2 = 3 − R
Solving these 2 equations you will get
R = 2 1 , X = 2
Finally,
R X × ( r + 3 y ) = 1 6