Put in your 2-cents worth -It's all in the penny-

Geometry Level pending

A penny rotates about a stationary quarter. The penny never loses contact with the quarter and does not slip in its rotation. The radius of the quarter is 5/4 that of the penny.

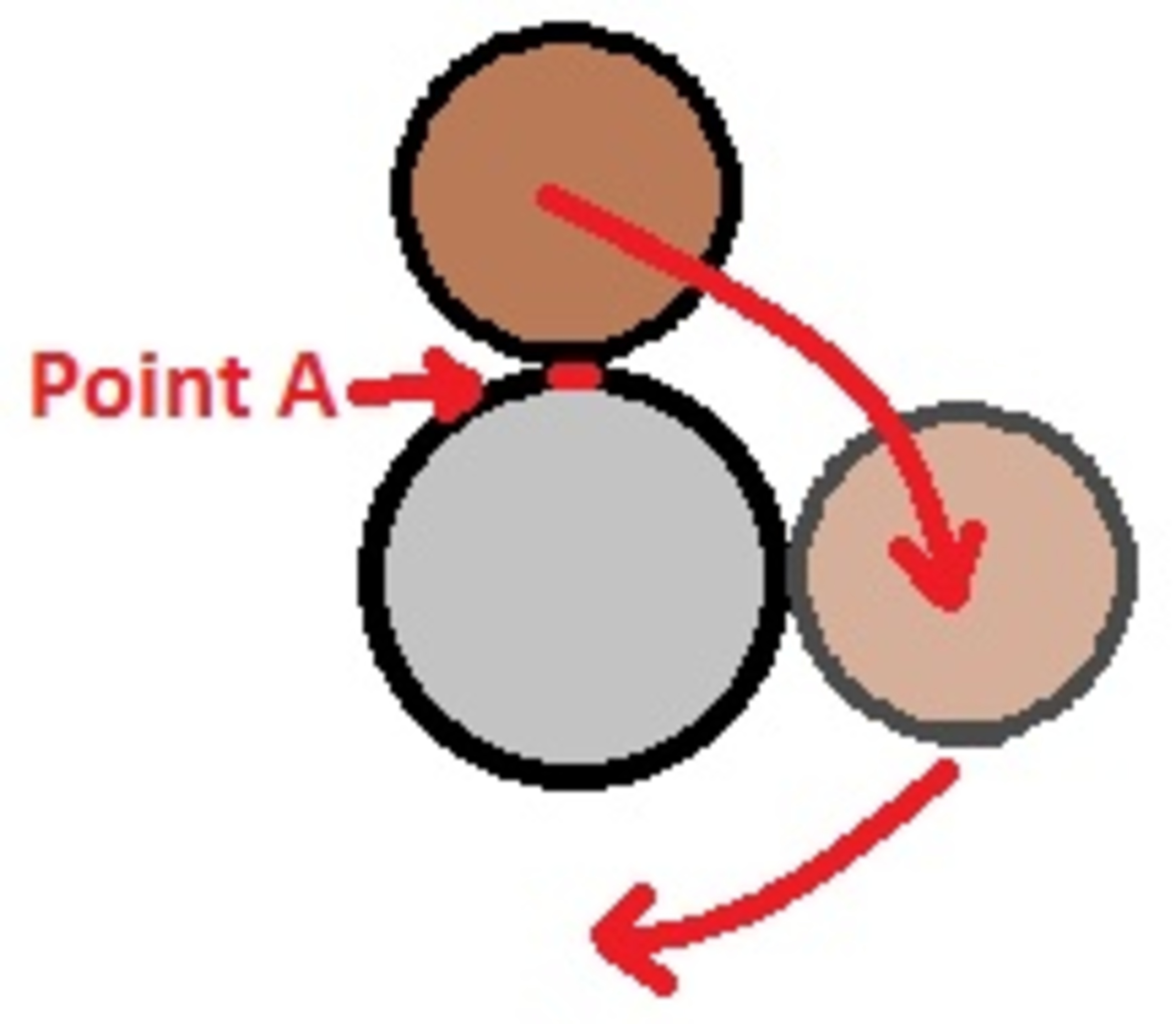
The penny rotates from point A on the quarter until it contacts the same point again. How many revolutions does the penny make in the time that it travels around the quarter?

Hint: Try to measure the number of revolutions a quarter would make if it rotated around a stationary quarter. (Do this physically)

The answer is 2.25.

1 solution

Jared Jones
Sep 11, 2015

The center of mass will move the same distance as the paint track left on the ground.

When a coin is rolled about another coin, the same principle holds true. The center of mass of the rotating coin moves in a concentric circle around the edge of the other coin. The distance traveled by the rotating coin is greater than the circumference of the other coin and thus the angular rotation is also greater.

The answer is a ratio of the sum of the radii to the penny's radius. 1.8/.8 = 2.25

Relevant question .

Pi Han Goh - 5 years, 9 months ago

Can we do the following :

G.P.E = K.E

mgh = $\frac{1}{2}$ m $v^{2} \Longrightarrow$ v = 7

Hence: w = v/r = $\frac{7}{\frac{5}{4}}$ = 5.6

Therefore: Frequency = 5.6 / (2 $\pi$ ) = 0.89

Time Period = 1 /f = 1.12

Please Help

Syed Baqir - 5 years, 9 months ago

No. This isn't a problem involving the gravitational or centripetal forces. The penny need not rotate around the quarter at any specific rate, only rotate all the way along the quarter without slipping and return to point A. Your procedure would be the basic setup for an object revolving in a perfect circle around a body in space due to the gravitational force exerted between the two objects. Another obvious reason for why such model fails to capture the situation is that it assumes zero friction.

Jared Jones - 5 years, 9 months ago

You are correct, But In Physics there are some limitations like:

if penny rotates around stationary corner then it will Only Rotate iff it have w "Rotational Speed" .

To find speed we do energy and it looks correct because question said from point A to point A again.

By the way are we supposed to find Rotation per minute or Rotation per second ?

Syed Baqir - 5 years, 9 months ago

@Syed Baqir – You need neither rotation per minute, nor rotation per second; the only thing that is needed is the revolutions the penny makes after it has completed its path around the quarter. The penny can rotate quickly or slowly. Its rotation speed can vary and it can still complete the path. Revolutions are complete rotations (2pi radians).

Jared Jones - 5 years, 9 months ago

@Jared Jones – hmm, Thanks ......... :D

Syed Baqir - 5 years, 9 months ago

Put in your 2-cents worth -It's all in the penny-

The answer is 2.25.

1 solution

0 pending reports