Pyramidal Mystery
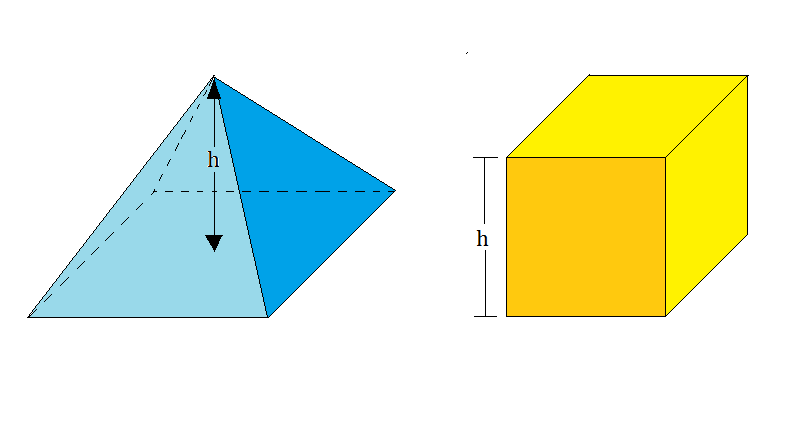
A square-based pyramid and a cube have the same surface area and height, as shown above. The pyramid's lateral surface consists of 4 equivalent triangles, where the heights of the triangle and the cube are co-prime integers.
What is the surface area of the pyramid?
The answer is 96.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let s be the side length of the square base of the pyramid. Then the height of the each lateral triangle is the hypotenuse of the right triangle, which has h and 2 s as the adjacent arms.
Hence, the triangle's height is h 2 + 4 s 2 .
It is given that the the surface area of the pyrimid is equal to the cube's surface area.
4 × 2 1 × s ( h 2 + 4 s 2 ) + s 2 2 s ( h 2 + 4 s 2 ) 4 s 2 ( h 2 + 4 s 2 ) = 3 6 h 4 − 1 2 ( h 2 ) ( s 2 ) + s 4 1 6 h 2 s 2 s h s = = = = = = 6 h 2 6 h 2 − s 2 4 h 2 s 2 + s 4 3 6 h 4 3 6 1 6 = 3 2 2 3 h
Then the height of the triangle = h 2 + 4 1 ( 2 3 h ) 2 = h 2 + 1 6 9 ( h 2 ) = 4 5 h .
Thus, the ratio of the triangle's height to the cube's height is 5 : 4 , and since these heights are co-prime, then h = 4 and the triangle's height = 5 .
And so s = 6 .
As a result, the pyramid's surface area = 6 2 + 4 × 2 1 × 5 × 6 = 9 6 .
Alternatively, the cube's surface area = 6 × 4 2 = 9 6 .