Pythagorean identities will just have to do
E = ∫ 0 π / 2 1 − sin ( 2 0 1 6 x ) d x
Find E .
Bonus: Generalize for ∫ 0 π / 2 1 − sin ( 1 2 n x ) d x , where n is a positive integer , and prove it.
The answer is 1.414213562.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Note another to find the integral of \rt(1-sinx) or is to multiply top and bottom by rt(1+sinx) which gives cosx/rt(1+sinx) which is an easy u sub to give 2rt(1+sinx)+C. Also works for rt(1-sinx)
sqrt(1 - sin 2016x) = abs(sin 1008x - cos 1008x), then treat as 504 separate integrations, each giving (2 x sqrt2)/1008). The first quarter cycle (0 to pi/4032) and the last three-quarter one can be treated as one whole cycle
Can you please explain how you got €=I/4
Log in to reply
I have changed the solution to explained it.
what if we make the integrand a perfect square an then simplify the two seperate integrals i.e (sin1008x-cos1008x)^2
It doesn' give the solutions even the integral calculator gives a different solution: CHECK THE FOLLOWING LINK BY PUTTING YOUR EXPRESSIONS...
https://www.symbolab.com/solver/definite-integral-calculator/%5Cint_%7B0%7D%5E%7B1.57%7D%5Csqrt%7B1-%5Csin%5Cleft(2016x%5Cright)%7Ddx
I'm trying to understand step 3 (dropping 2 k π due to periodicity and having k pop out of integral) and step 6, where we get cos out instead of sin. Any help?
Hello, first of all, I know I am wrong, but I am writing in order to somebody tells me where is my fail.
The primitive I achieve is 1008(Sqrt(1+sin(2016x)) and if we take the values x=0 and x=Pi/2, we obtain 0 as a result, which is absolutely false since the function is always positive. I know I am making a mistake, but I am not sure where...maybe in the process where cos(2016x) is involved?
Thank you for your help!!
Lemme just
E = ∫ 0 2 π 1 + sin ( 4 n x ) 1 − sin ( 4 n x ) 1 + sin ( 4 n x ) d x = ∫ 0 2 π 1 + sin ( 4 n x ) ∣ cos ( 4 n x ) ∣ d x sin ( 4 n x ) is periodic over 2 n π . = n ⋅ ( ∫ 0 8 n π 1 + sin ( 4 n x ) cos ( 4 n x ) d x − ∫ 8 n π 8 n 3 π 1 + sin ( 4 n x ) cos ( 4 n x ) d x + ∫ 8 n 3 π 2 n π 1 + sin ( 4 n x ) cos ( 4 n x ) d x ) t = sin ( 4 n x ) ⇔ d t = 4 n cos ( 4 n x ) d x = n ⋅ 4 n 1 ( ∫ 0 1 1 + t 1 d t − ∫ 1 − 1 1 + t 1 d t + ∫ − 1 0 1 + t 1 d t ) = 4 1 ( [ 2 1 + t ] 0 1 + [ 2 1 + t ] − 1 1 + [ 2 1 + t ] − 1 0 ) = [ 1 + t ] − 1 1 = 2 .
You have to justify the first step.
Log in to reply
What do you mean?
Log in to reply
It's not clear how my original integral is equal to his/her first line. S/he skipped some important steps here.
Log in to reply
@Hobart Pao – I don't see what's skipped.
I just multiplied 1 + sin ( 4 n x ) to the numerator and denominator,
and used the identity 1 + sin ( 4 n x ) 1 − sin ( 4 n x ) = 1 − sin 2 ( 4 n x ) = cos 2 ( 4 n x ) = ∣ cos ( 4 n x ) ∣ .
Log in to reply
@Boi (보이) – Nevermind, I'm stupid...sorry.
Log in to reply
@Hobart Pao – It's okay!
And nah you're not, everyone makes mistakes ^^;
E = ∫ 0 2 π 1 − sin ( 4 k x ) d x = 4 k 1 ∫ 0 2 k π 1 − sin θ d θ = 4 k k ∫ 0 2 π 1 − sin θ d θ = 4 1 ( ∫ 0 π 1 − sin θ d θ + ∫ π 2 π 1 − sin θ d θ ) = 4 1 ( 2 ∫ 0 2 π 1 − sin θ d θ + 2 ∫ π 2 3 π 1 − sin θ d θ ) = 2 1 ( ∫ 0 2 π 1 − sin ( 2 π − θ ) d θ + ∫ π 2 3 π 1 − sin ( 2 π − θ ) d θ ) = 2 1 ( ∫ 0 2 π 1 − cos θ d θ + ∫ π 2 3 π 1 − cos θ d θ ) = 2 1 ( ∫ 0 2 π 2 sin 2 θ d θ + ∫ π 2 3 π 2 sin 2 θ d θ ) = 2 ( cos 2 θ ∣ ∣ ∣ ∣ 2 π 0 + cos 2 θ ∣ ∣ ∣ ∣ 2 3 π π ) = 2 ( 1 − 2 1 + 0 + 2 1 ) = 2 Let θ = 4 k x ⟹ d θ = 4 k d x Since the integrand has a period of 2 π See note. Since sin θ is symmetrical about 2 π and 2 3 π Using identity ∫ a b f ( x ) d x = ∫ a b f ( a + b − x ) d x Since cos 2 u = 1 − 2 sin 2 u
We note that the result applies to all multiples of 4, which 2016 is one. Therefore, ⟹ ⌊ 1 0 0 0 E ⌋ = 1 4 1 4
Note: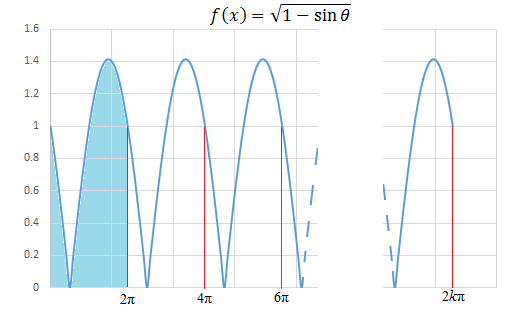
The figure is a plot of f ( x ) = 1 − sin θ , we note that the area under the curve from 0 to 2 k π or k cycles is the same as the area under the curve from 0 to 2 π or 1 cycle multiplies by k .
⟹ ∫ 0 2 k π f ( x ) d x = k ∫ 0 2 π f ( x ) d x