Quadrilateral in a Cubic Polynomial
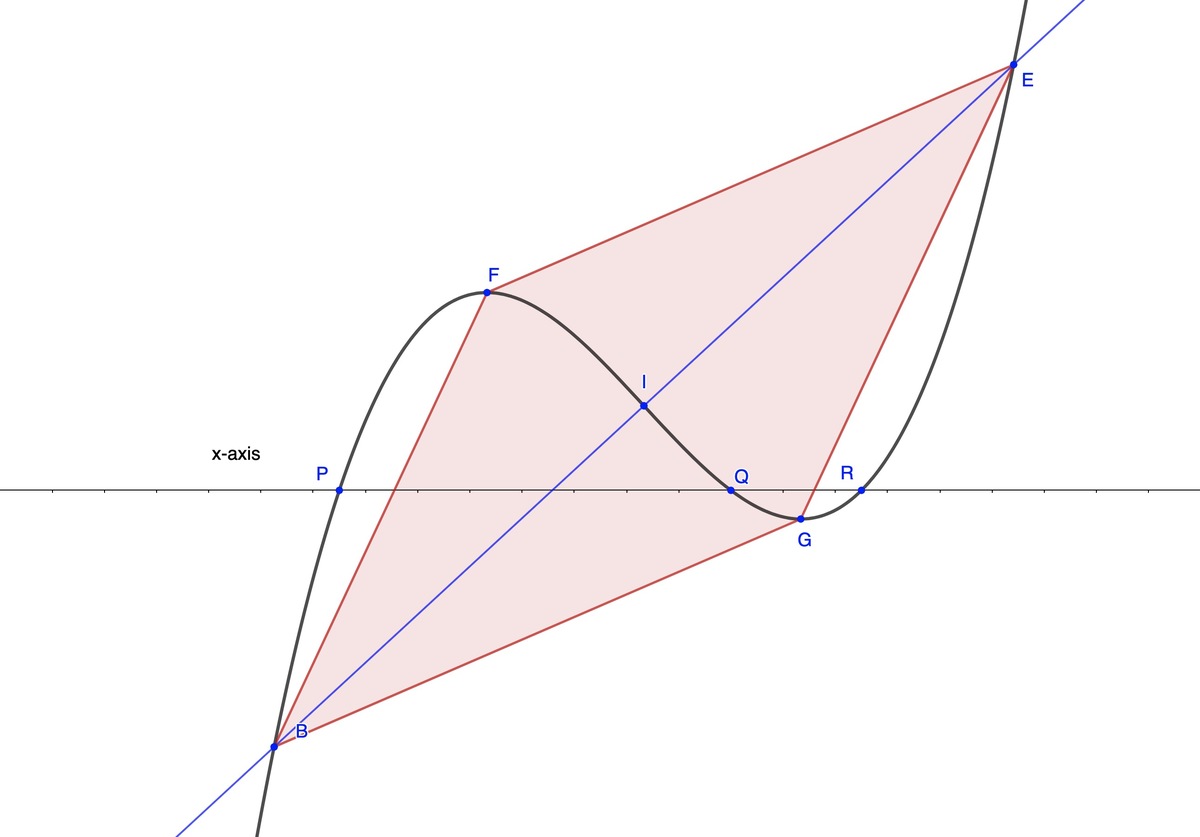
A monic polynomial of degree 3 has three unique integer roots, P,Q and R between 0 and 36 inclusive. A quadrilateral BFEG has been constructed as follows: F and G are the two extrema and I is the inflection point. The blue line is normal to the curve at I. This normal intersects the polynomial in two additional places, B and E.
If the minimum area of the quadrilateral can be expressed as c a b , where a and c are coprime and b is square free, then provide the sum a + b + c .
The answer is 25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
NIce solution! A slip of the pen: x = 3 1 ( P + Q + R ) .
Here is my computer assisted solution heavily relying on sympy module for python.
I consider a polynomial f L , R ( x ) = ( L + x ) x ( x − R ) , where L and R are some natural numbers (i.e. I shift the polynomial from the problem in such a way, that 0 is its middle root).
After few calculations (cf. code below) it turns out, that the area of the quadrilateral of our interest expressed as a function of L and R has the form: A ( L , R ) = 8 1 ( L 2 + L R + R 2 ) 2 3 L 4 + 2 L 3 R + 3 L 2 R 2 + 2 L R 3 + R 4 + 9 ( 2 L 4 + 4 L 3 R + 6 L 2 R 2 + 4 L R 3 + 2 R 4 + 2 7 ) . It attains its minimum for L = R = 1 . The minimal value is 9 1 0 6 , which gives the answer 25.
And the code:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |
|
Nice use of sympy.
As Mark Hennings has already pointed out in his solution, the cubic has order 2 rotational symmetry about its point of inflection I , hence, the quadrilateral is a parallelogram. Working in 2D, its area A can be given by A = ∣ ∣ ∣ det ( F E , F B ) ∣ ∣ ∣ .
We notice that a translation of the cubic by vector I O , ( O is the origin) does not affect the compound shape of the cubic and the parallelogram, but it simplifies quite a bit the algebraic manipulations needed.
Due to the symmetry, the zeros of the translated cubic
g
are
0
,
±
c
for some positive real number
c
.
Hence,
g
(
x
)
=
x
(
x
2
−
c
2
)
=
x
3
−
c
2
x
.
Consequently,
g
′
(
x
)
=
3
x
2
−
c
2
⇒
g
′
(
0
)
=
−
c
2
⇒
slope of
B
1
E
1
=
c
2
1
⇒
equation of
B
1
G
1
:
y
=
c
2
1
x
.
To find points
E
1
and
B
1
, we solve simultaneously
{
y
=
c
2
1
x
y
=
x
3
−
c
2
x
and we easily get
E
1
(
c
c
4
+
1
,
c
3
c
4
+
1
)
,
B
1
(
−
c
c
4
+
1
,
−
c
3
c
4
+
1
)
.
For the point
F
1
,
g
′
(
x
)
=
0
⇔
3
x
2
−
c
2
=
0
⇔
x
<
0
x
=
−
3
c
g
(
−
3
c
)
=
(
−
3
c
)
3
−
c
2
(
−
3
c
)
=
3
3
2
c
3
⎭
⎬
⎫
⇒
F
1
(
−
3
c
,
3
3
2
c
3
)
Thus, F 1 E 1 = ( c c 4 + 1 + 3 c , c 3 c 4 + 1 − 3 3 2 c 3 ) and F 1 B 1 = ( − c c 4 + 1 + 3 c , − c 3 c 4 + 1 − 3 3 2 c 3 ) .
Finally, A = ∣ ∣ ∣ det ( F E , F B ) ∣ ∣ ∣ = ∣ ∣ ∣ det ( F 1 E 1 , F 1 B 1 ) ∣ ∣ ∣ = 3 2 c 4 + 1 ( 3 2 c 2 + c 2 1 ) .
Now, due to the concavity of the cubic, the distance between
P
and
R
cannot exceed the length of segment
M
N
, which is parallel to the x-axis, through the point of inflection
I
.
Hence,
2
⩽
R
−
P
⩽
M
N
=
L
K
=
2
c
. Thus,
c
⩾
1
.
If we label c 2 = x , we have a function for the area of the parallelogram: A ( x ) = 3 2 x 2 + 1 ( 3 2 x + x 1 ) , x ⩾ 1 . For x ⩾ 1 , A ′ ( x ) = 3 3 x 2 x 2 + 1 2 ( 4 x 4 + 2 x 2 − 3 ) > 0 . Thus, A ( x ) is increasing, so A min = A ( 1 ) , which occurs when c = 1 2 = 1 .
Since 2 ⩽ R − P ⩽ 2 c = 2 , it turns out that the zeros P , Q , R of the initial cubic are three consecutive integers, i.e. ( P , Q , R ) ∈ { ( 0 , 1 , 2 ) , ( 1 , 2 , 3 ) , … , ( 3 4 , 3 5 , 3 6 ) } No matter which triad is the actual zeros of the cubic, the minimum area of the parallelogram is A ( 1 ) = 9 1 0 6 .
For the answer, a = 1 0 , b = 6 , c = 9 , hence, a + b + c = 2 5 .
the area asked will be minimum when the three zeros of the polynomial are the closest. So, let us choose the polynomial y = x ( x − 1 ) ( x − 2 ) = x 3 − 3 x 2 + 2 x .
So the coordinates of I are ( 1 , 0 ) obtained from the condition d x 2 d 2 y = 0 and the equation of the curve.
Coordinates of F and G are ( 3 3 − 3 , 9 2 3 )
and ( 3 3 + 3 , 9 − 2 3 ) respectively, obtained from the condition d x d y = 0 and the equation of the curve.
Slope of B E is 1 , and it's equation is y = x − 1 . Solving this and the equation of the curve we get the coordinates of B and E as
( 1 − 2 , − 2 ) and ( 1 + 2 , 2 ) .
Hence the required area is 9 1 0 6 , a = 1 0 , b = 6 , c = 9 and a + b + c = 1 0 + 6 + 9 = 2 5 .
I have the same solution. But "the area asked will be minimum when the three zeros of the polynomial are the closest" it is open question. I try оther a,b,m for polynom mx(x-a)(x-b) and see that minimum area for m=1, a=1, b=2.
Log in to reply
So the proposition is justified. Isn't it? The area is minimum when the three zeros are closest!
Log in to reply
Yes minimum when the three zeros are closest - but I have no rigorous justification for it.
Log in to reply
@Yuriy Kazakov – See my proof for why the area is minimized when the roots are consecutive.
What about a coefficient in front of your polynomial? When considering y = a x ( x − 1 ) ( x − 2 ) , there are smaller values for the area than A = 9 1 0 6 ≈ 2 . 7 2 2 for different values of a . The smallest I found was when a = 2 3 + 5 7 , which leads to an area of A = 1 8 1 8 5 8 + 1 1 4 5 7 ≈ 2 . 3 0 3 . I think the question is flawed, and should include that the polynomial must be a monic polynomial (where the leading coefficient is 1 ).
Log in to reply
Quite right. I've edited it. Thank you!
Fine rezult.
I've just come and so sorry for not answering you. Yes. That is the truth. Because of excitement, I missed the constant factor :).
Is this college mathematics?
Log in to reply
Yes, I would say so. This problem would be difficult to do without using derivatives, which is taught in Calculus. Calculus is a college class, although some advanced students do take Calculus in their last years of high school.
Ok , that is why i couldn't solve this
Since a cubic has order 2 rotational symmetry about its point of inflection, the quadrilateral is a parallelogram, and hence has area ∣ ∣ ∣ B F × B G ∣ ∣ ∣ Suppose that the polynomial has distinct integer roots P < Q < R , and hence is ( X − P ) ( X − Q ) ( X − R ) . It is easy to evaluate the coordinates of F and G , and to solve the equation of the cubic simultaneously with that of the normal to the cubic at I (where x = 3 1 ( P + Q + R ) ) to find the coordinates of B - both of these calculations simply require us to solve quadratics. After much algebra and simplification, we obtain the surprising result that the area of the quadrilateral is A ( X ) = 2 7 3 X 2 ( 2 7 + 2 X 2 ) 9 + X 2 where X = P 2 + Q 2 + R 2 − P Q − P R − Q R We note that 2 X = ( Q − P ) 2 + ( R − Q ) 2 + ( R − P ) 2 ; since Q − P , R − Q ≥ 1 and R − P ≥ 2 we see that X ≥ 3 for all allowed values of P , Q , R . Moreover d X d A = 2 7 3 X 2 9 + X 2 2 ( 4 X 4 + 1 8 X 2 − 2 4 3 ) and hence d X d A > 0 for all X ≥ 3 . Thus the smallest possible value of A occurs when X = 3 , which happens when P , Q , R are consecutive integers. The minimum value of A is thus 3 1 0 3 2 = 9 1 0 6 , making the answer 1 0 + 9 + 6 = 2 5 .