Quadrilaterals are back!

Probability Level 3

Figure the total number of quadrilaterals in the given figure.

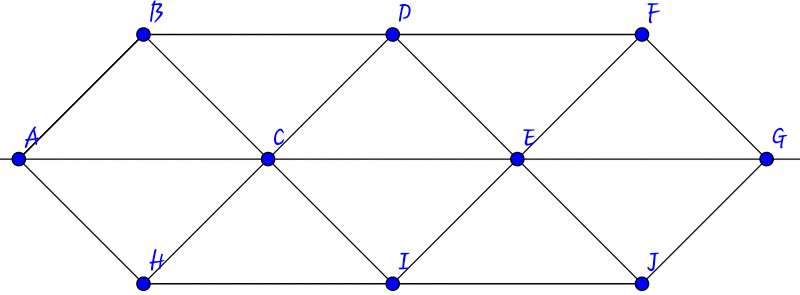
There are two defined points (C and E) on line segment AG. There is one defined point (D) on line segment GF. There is one defined point (I) on line segment HJ.

Structure:-
B is connected to A and C by line segments.
D is connected to C and E by line segments.
F is connected to E and G by line segments.
H is connected to A and C by line segments.
I is connected to C and E by line segments.
J is connected to E and G by line segments.

Clarification:- BI , DJ, HD and FI are straight lines.

The answer is 33.

1 solution

Ashish Menon
Apr 17, 2016

In figure ABFG, there are $10$ quadrilaterals.
In figure AGJH, there are $10$ quadrilaterals.
Then the only quadrilaterals which are left are :- ABDH, CDFI, DEIH, FGJI, JGFE, JGFD, IEDC, IEDB, HCBA, BAIH, DJIC, IJDB and HDFI.
$\therefore$ The total number of quadrilaterals = $\boxed{33}$ .

you are wrong $29$ is not the correct answer.

Atul Shivam - 5 years, 1 month ago

Oh my gosh, can you explain how?

Ashish Menon - 5 years, 1 month ago

See the report!!!

Atul Shivam - 5 years, 1 month ago

@Atul Shivam – See the comment to your report!!! :P

Nihar Mahajan - 5 years, 1 month ago

Your answer is still incorrect

I am agree with you that total number of quadrilateral that can be formed from ABFG &AGJH is 10+10=20

But let me confirm that quadrilateral left are $ABCH,CDEI,EFGJ,ABDH,ABIH,BIED,HIED,CDFI,CDJI, DFGJ, IFGJ,BDJI,DFIH$ which is 13 in numbers so total quadrilateral possible are $20+13=\boxed{33}$

Atul Shivam - 5 years, 1 month ago

I forgot those 4, ok ill post a report

Ashish Menon - 5 years, 1 month ago

Don't delete the problem because of this, thanks.

Nihar Mahajan - 5 years, 1 month ago

@Nihar Mahajan – Yes, thanks

Ashish Menon - 5 years, 1 month ago

U forgot 4 quadrilateral

Atul Shivam - 5 years, 1 month ago

Quadrilaterals are back!

The answer is 33.

1 solution

0 pending reports