Quady Areas
In both of the quadrilaterals (a rectangle and a parallelogram) below, four inner segments extended from the four vertices form a rectangle in the center. At the same time, two congruent triangles are generated on opposite sides.
Must this only occur in rectangles and parallelograms?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
As shown, we could start out with almost any (inner) rectangle, attach 2 (large enough) congruent triangles, and then connect up the 4 points.
This gives us a quadrilateral which 2 opposite sides that are equal in length, but it need not be an isosceles trapezoid.
It is also clear that it is a necessary condition that the quadrilateral must have 2 opposite sides that are equal in length.
Is this condition sufficient? Namely, given any quadrilateral with 2 opposite sides that are equal in length, can we partition the inner rectangle and triangles accordingly?
Log in to reply
I don't think it is possible for an isosceles trapezoid with base angles that are less than or equal to 45°. Two congruent right triangles with at least one set of parallel lines will necessarily have one right angle outside or on the trapezoid.
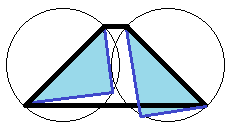
Log in to reply
If you drop perpendiculars from the top side, that gives us the degenerate case where the inner rectangle is a line, so I don't consider this a "true" counterexample.
Log in to reply
@Calvin Lin – This quadrilateral has a rectangle that is partly outside the rectangle.

The congruent sides have slopes of m and − m , where m < 1 , and one of the top angles of the quadrilateral is nearly (but not quite) a straight line.
However, if we allow for rectangles that are partly outside or on the original quadrilateral, then I believe that any two congruent sides can be partitioned accordingly by the following method: make two congruent circles with the given congruent sides A D and B C as diameters, extend A D and B C until they meet at G , create the bisector G H of the two extensions, create A E and B F parallel to G H such that E and F are on the two congruent circles, and create two congruent triangles △ A E D and △ B F C .

Since A D and B C are diameters of the circle, both ∠ A E D and ∠ B F C are right angles. As corresponding angles to bisected angles, ∠ D A E ≅ ∠ D G H ≅ ∠ C G H ≅ ∠ C B F . Therefore, the two triangles are congruent by AAS congruency. The parallel sides and right angles can then be used as a guide to draw the interior rectangle.
The two white triangles in your example are not congruent.
Log in to reply
The blue shaded triangles are.
Log in to reply
Just re-read the question. So only one of the pairs of triangles needs to be congruent. Makes sense now.
The blue shaded triangles are not congruent because their hypotenuses are of different size. They are just similar. Mangoreba
Log in to reply
@Napoleone Cavlan – The blue shaded triangles are congruent. One was copied, pasted, and rotated from the other.
One thing that confused me was that it wasn't clearly stated what was meant by a rectangle in the center. So, is the central rectangle required to land driectly on the geometric center of the starting quadrilateral or does it just need to be somewhere inside?
This is not a "Basic "level" math puzzle. There are too many considerations to have to look after.
How did you come up with this?
Log in to reply
I started with the congruent triangles, positioned them so two of their sides were parallel (to make the inner rectangle) and slid them until the outer quadrilateral was not a parallelogram.
u are so good
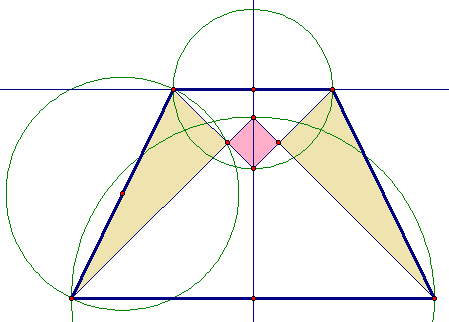
I'm not exactly sure what is allowed, but here is a solution using an isosceles trapezoid. The tan triangles are congruent and the pink quadrilateral is a square.
I left blue lines that I used to ensure an iso. trap. and the green circles that ensure the right angles.
Correct. I want to make this problem more generic, so the solvers can experiment with polygons.
I thought you meant that there would be two pairs of congruent triangles not just one.
I didn’t really understand the question, the way it’s worded. I thought it meant 2 pairs of triangles, which has to be a parallelogram I believe.
Rectangle is a parallelogram, so if it works for parallelogram, it has to be valid for rectangle. Then we can tell that it works for rhombus and square. Why these answers are not acceptable?
Log in to reply
Rhombus and square are also parallelograms and the question asks for another type of quadrilateral which satisfies the given conditions.
Log in to reply
I agree with you but a rectangle is not the another type of quadrilateral. Why then the question states " only in these two cases " ? On my opinion, it has to be "only in one case- parallelogram".
Ha ha. The two congruent triangles must have a corner of 90 degrees in the middle, or else figure in the center wouldn't be a rectangle. But that only necessarily leads to a parallelogram if the two sides that make that angle are equal (obviously) or when the triangles are just 180 degrees rotated (that is, they are not each others mirror image).
I said 'ha ha' because the given image suggests that they can't be their mirror image, but I didn't fall for that :p. Can't make a pretty image, but David Vreken already gave a picture with two congruent triangles that are each others mirror image, so...
How is David Vreken's a proper solution? It does not have two mirrored triangles.
Start with a central rectangle and extend each side outwards. Adjust the length of these extensions so that two of the adjacent 'lengths' are in the same proportion to each other as the other two adjacent 'lengths'. (This, along with the common right angle, will ensure that congruent triangles are generated.) Then join the outer points of the extensions together to form a quadrilateral.
NB I'm using 'length' in a rather vague way. Strictly speaking one side of the triangle will be the length of the extension, the other will be the length of the extension plus the side of the rectangle. It helps to look at the diagram.
Here is another counter-example: