Ques. -24

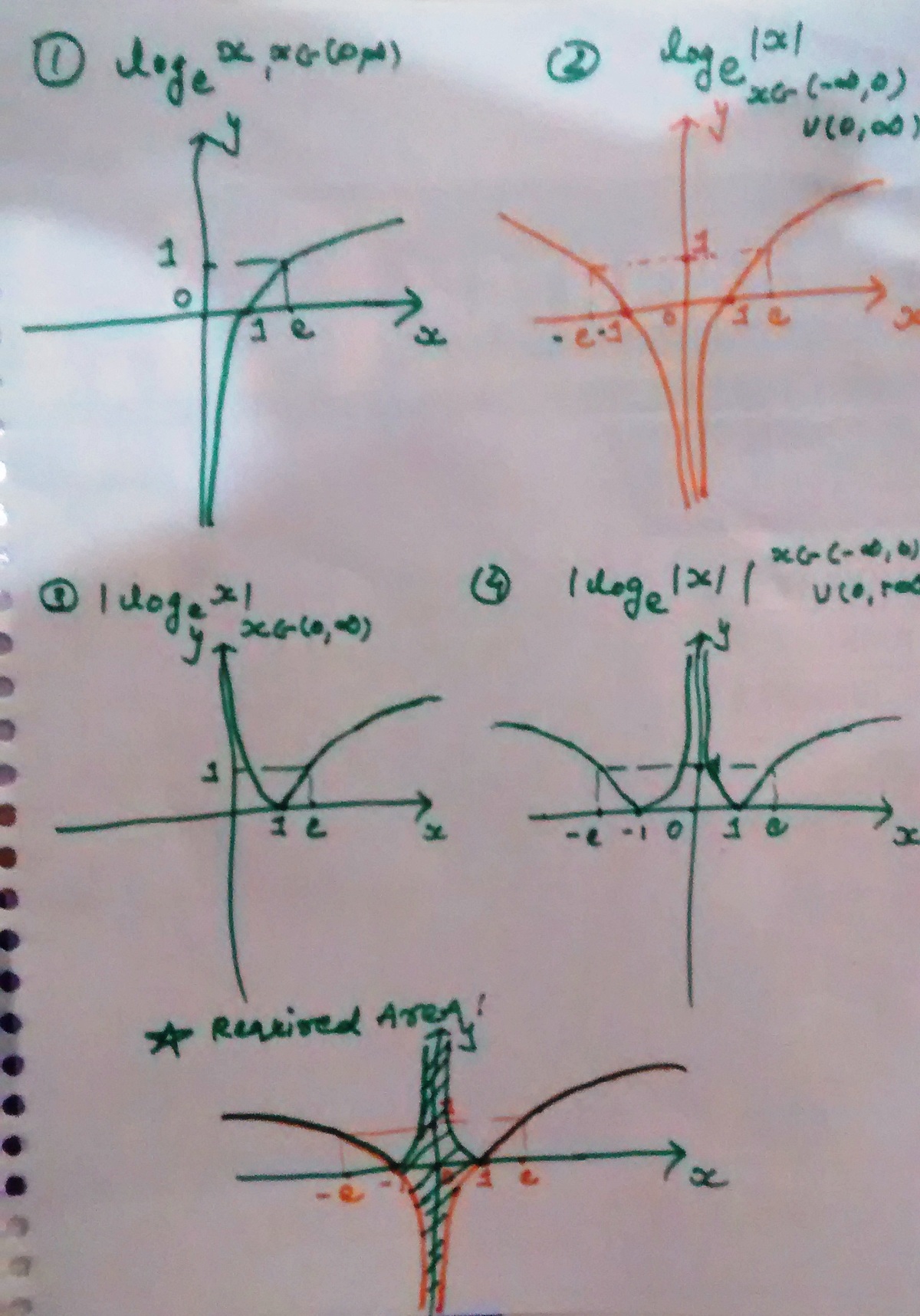manish bhargao These are the graphs

The area is 4 times the area bounded by y=ln(x) between 0 and 1.Now if you remember integral lnx=x(lnx-1)+c,it could save some time.Even better would be to use the fact that lnx is inverse of e^x and inverse functions are mirror images in the line y=x.and hence required area =4 times integral e^x between limit negative infinity and 0

Basically, this will look like the graph of $ln(x)$ , but it's flipped and rotating. We need to find the absolute value of the area bounded between 0 and 1 of $ln(x)$ .

Integrating $ln(x)$ with indefinite integral for now since im too lazy to put the bounds on every integral sign (excuse my lack of +C's).

Important note: $\int e^x=e^x+C$

$\displaystyle \int \ln(x) ~~dx$

let $x=e^u$ and $dx=e^u ~~ du$

$\displaystyle \int \ln(e^u) e^u~~du$

$\displaystyle \int u e^u~~du$

Integrating by parts $\displaystyle \int a~ db=ab-\displaystyle \int b ~da$ . Let $a=u,~~da=1,~~db=e^u,~~b=e^u$

$ab-\displaystyle \int b ~da=ue^u-\displaystyle \int e^u$

$ue^u-e^u$

Re substituting for u. Lol, I'm substituting for "u". Haha, ha, anyone? Never mind

$x=e^u \Rightarrow \therefore u=\ln x$

$ln(x)e^{\ln(x)}-e^{\ln(x)}$

$x\ln(x)-x$

Now, we need the definite integral from 0 to 1, so plugging in x=0 will by some magical witch craft=0. When x=1, we have our integral equal to -1. We need the absolute area so we can let it be 1.

Finally, we multiply this by 4 since there are 4 of these figures.

This our answer is 1x4=4.