Dividing Diamonds
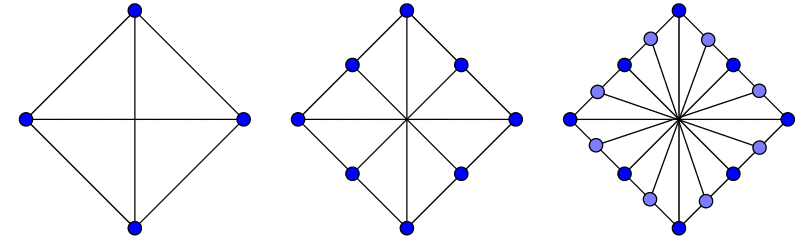
If the figure in the left is named figure 1, the one in the middle is named figure 2 and the one in the right is named figure 3, then find the number of triangles in the 1 2 th figure that follows this pattern.
The answer is 8392708.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Note to all solutuon readers, this rule does not work for figure 1,2. The reason for the mention in the question was to fulfill the pattern. ;)
The number of triangles of n-th figure is 4 ( 2 2 n − 1 × ( 2 n − 1 + 1 ) ) + 4
Observe that the figure is symmetric, so we can calculate in a quarter and then multiply by 4 . Also, add 4 to the result because there are 4 "half-square"s haven't been counted.
In a quarter of 1 st figure there are 2 0 = 1 small triangle.
In a quarter of 2 nd figure there are 2 1 = 2 small triangles. The number of triangles (including larger ones) in this quarter is: 2 + ( 2 2 ) = 3 .
In a quarter of n th figure there are 2 n − 1 small triangles. The number of triangles (including larger ones) in this quarter is: 2 n − 1 + ( 2 2 n − 1 ) .
So, mulitply it by 4 and add 4 gives us: 2 n + 1 + 4 × ( 2 2 n − 1 ) + 4 .
Hence, in the 1 2 th figure, the answer should be 2 1 3 + 4 × ( 2 2 1 1 ) + 4 = 8 3 9 2 7 0 8 .
But the answer to this question is different. Am I wrong at somewhere?
Yes, there is one mistake, by following your method, we would get 7 triangles in quarter of figure 3, while there are 10 of them.
Log in to reply
Wait, 2 2 + ( 2 2 2 ) = 1 0 , it's correct.
Log in to reply
First of all, you have mentioned that the formula is 2 n + 1 + 4 × ( 2 2 n − 1 ) + 4 , then you should add 2 4 not 2 2 , right?
Log in to reply
@Ashish Menon – It's the formula to calculate number of triangles in total. Apply the formula with n = 3 gives us 4 4 .
What I'm mentioning is the formula to calculate in a quarter only. It's 2 n − 1 + ( 2 2 n − 1 ) . Apply the formula with n = 3 gives us 1 0 , which is correct due to the figure.
Observe that in n th case the number of quadrilaterals is given by the formula:-
4 × ( i = 1 ∑ i = 0 ∑ n − 2 2 i i ) + 4
So, in the 2 0 1 6 th figure there would be 4 × ( i = 1 ∑ i = 0 ∑ 2 0 1 4 2 i n ) + 4
= 8384516 triangles. □