Question marks on my intelligence!
1 0 0 , 9 5 , ? , 7 9 , 6 8 , ? , 4 0 , 2 3
What is the sum of the numbers that should replace the question marks?
Check your IQ level through the test : IQ Test
The answer is 143.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
Discussions for this problem are now closed
Just a more formal solution. We first note the following recurrence for the given sequence (denote by a n the n th term of the sequence),
a n − 1 − a n = 2 n + 1 , n ≥ 2
This is a very simple recurrence which can be solved as follows:
a n = c − i = 1 ∑ n ( 2 i + 1 ) ⟹ a n = c − n ( n + 1 ) − n ⟹ a n = c − n ( n + 2 ) , where c is some constant.
Now, using the initial value a 1 = 1 0 0 , we get c = 1 0 3 and the closed form of the recurrence as,
a n = 1 0 3 − n ( n + 2 ) , n ≥ 1
Using this, we need to find a 3 and a 6 . We get a 3 = 8 8 and a 6 = 5 5 and hence the answer is the sum 8 8 + 5 5 = 1 4 3
Why didn't you write a solution instead. Anyways, nice formal approach. :)
Meh, it works. It doesn't matter if it's a comment or a solution as long as it gets upvoted and appreciated by others. :D
"as long as it gets upvoted and appreciated by others"
You want upvotes and appreciation . But you don't want the better way in which you can have it.
Nice approach again...
;)
@Soumo Mukherjee – Well, atleast one person (you) appreciated it. That's more than enough for me.
What the hell is "n" here :-\
n is an indexing variable for the recurrence relation and we use it here to denote the term no. of the sequence.
Isn't that quite absurd..
Which part of my solution (approach) seems absurd to you?
@Sandeep Bhardwaj sir there can't be any question marks on your intelligence .
UPVOTED !!!
Upvoted ( your solution) !
hahaha... thank you. :)
i also did the same way
Wow! You guys are just awesome , this pattern struck me after about a minute of looking at it .
Then follow me!!
Just kidding..... i'm the one who is following you :)
Btw start learning Calculus dude , there are other 15 year olds who have started doing that , don't get left behind !
@A Former Brilliant Member – i know differentiation, i'm quite good in derivatives but i do not know integration yet, and that's the problem
better idea
just simple answer, there is sequence 100, 95, ... , 79, ... , 40, 23. then we find the difference between how much of the previous tribe with tribe that we want to find. 1st : 100. 2nd 100 to 95 we certainly think that the solution is
1
0
0
−
5
. 3rd : 95 to
?
we don't know. 4th :
?
to 79 we don't know. 5th : 79 to 68 is the difference was 11
7
9
−
6
8
. 6th : 68 to
?
we don't know. 7th :
?
to 40 we don't know. 8th : 40 to 23 is the difference was 17. so we can conclude that the next number will be obtained by reducing the number previously with odd numbers starting from 5 onwards.
1
0
0
,
(
1
0
0
−
5
)
,
(
9
5
−
7
)
,
(
8
8
−
9
)
,
(
7
9
−
1
1
)
,
(
6
8
−
1
3
)
,
(
5
5
−
1
5
)
,
(
4
0
−
1
7
)
1
0
0
,
9
5
,
8
8
,
7
9
,
6
8
,
5
5
,
4
0
,
2
3
then sum : 88 + 55 =
1
4
3
I came to 2 ideas, one was like most of you did, then got 88 and 55 then come to this 100-5x1=95, 100-6x2=88,100-7x3=79,100-8x4=68,100-9x5=55,100-10x6=40,100-11x7=23 and got same numbers.
T(n) = 103 - n(n + 2)
T(3) = 88
T(6) = 55
88 + 55 = 143
The n t h term appears to be 1 0 4 − ( n + 1 ) 2 . The missing 3 r d and 6 t h terms are 1 0 4 − 4 2 = 8 8 and 1 0 4 − 7 2 = 5 5 , and their sum is 1 4 3 .
You should show how you came to that conclusion!
Hint: If you see my comment on the topmost solution, you'll see that the closed form comes out as,
a n = 1 0 3 − n ( n + 2 ) , n ≥ 1
Expand the RHS and use the method of completing the square.
It is a fun fact to know that the sum of the first n odd positive integers is n 2 ;) It would have been more "user friendly" to write the sequence as 104, 103, 100, 95, 88,... ; then most people would have recognized that we are subtracting squares rather than working with a cumbersome recursive formula.
Ah yes! I missed that earlier. Upvoted your comment. :)
The pattern isn't apparent; we still have to find it. Looking at the differences of 95 and 79, 79 and 68, then 68 and 40, we get 16, 11 and 28, respectively. So the pattern of difference goes from 5, ?, ?, 11, ?, ? and 17. The distance between 95 and 79 is 16, getting the half of that would yield 8. The distance between 68 and 40 is 28, getting the half of that would be 14. Suspecting that all the differences are odd I got the odd numbers surounding 8 (7,9) and 16 (13,15). So the pattern is completed as 5,7,9,11,13,15,17.
95 - 7 = 88; 68 - 13 = 55
88 + 55 = 143
The no. decreases by 5,7,9....17 Then 88+55= 143
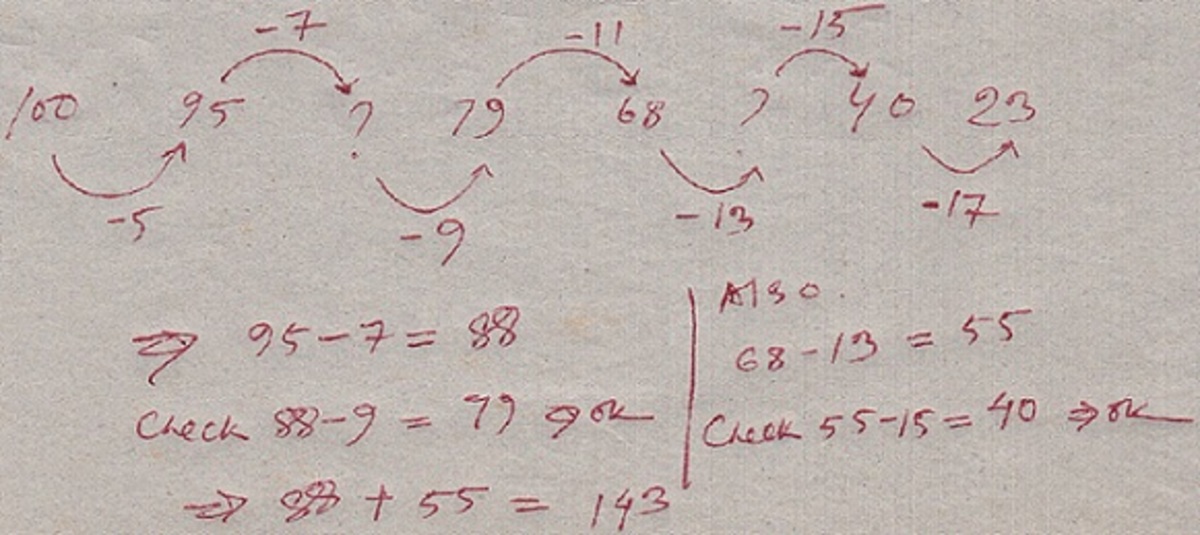
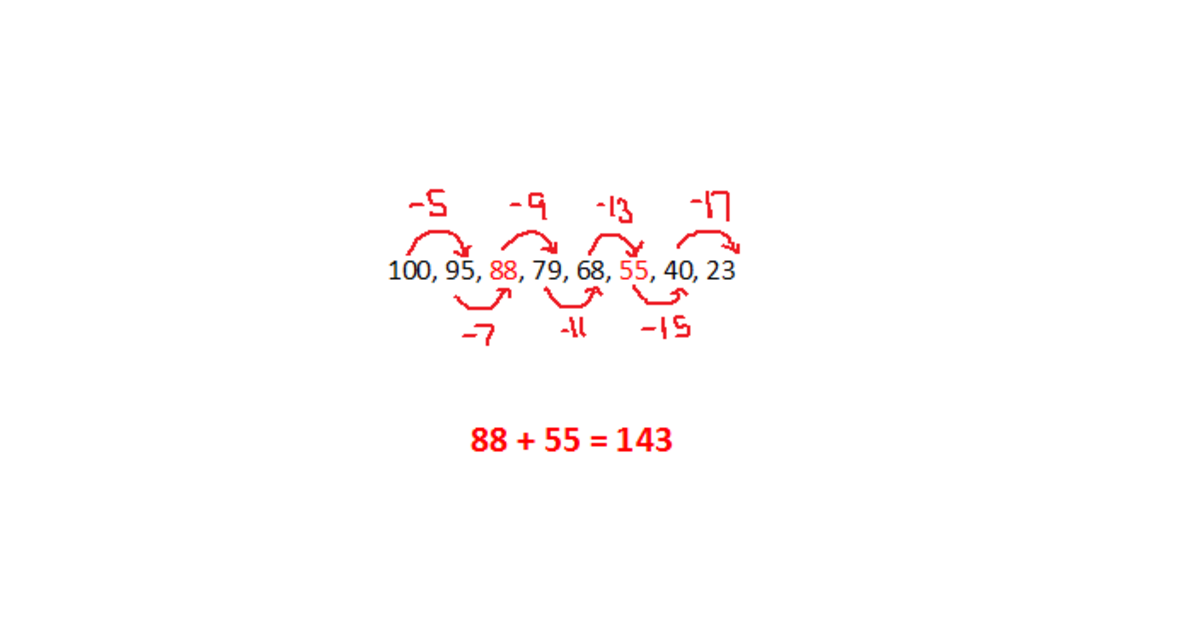
1 0 0 − 5 = 9 5 − 7 = 8 8 − 9 = 7 9 − 1 1 = 6 8 − 1 3 = 5 5 − 1 5 = 4 0 − 1 7 = 2 3
Hence 8 8 + 5 5 = 1 4 3