Quick and cute summer Sangaku #9
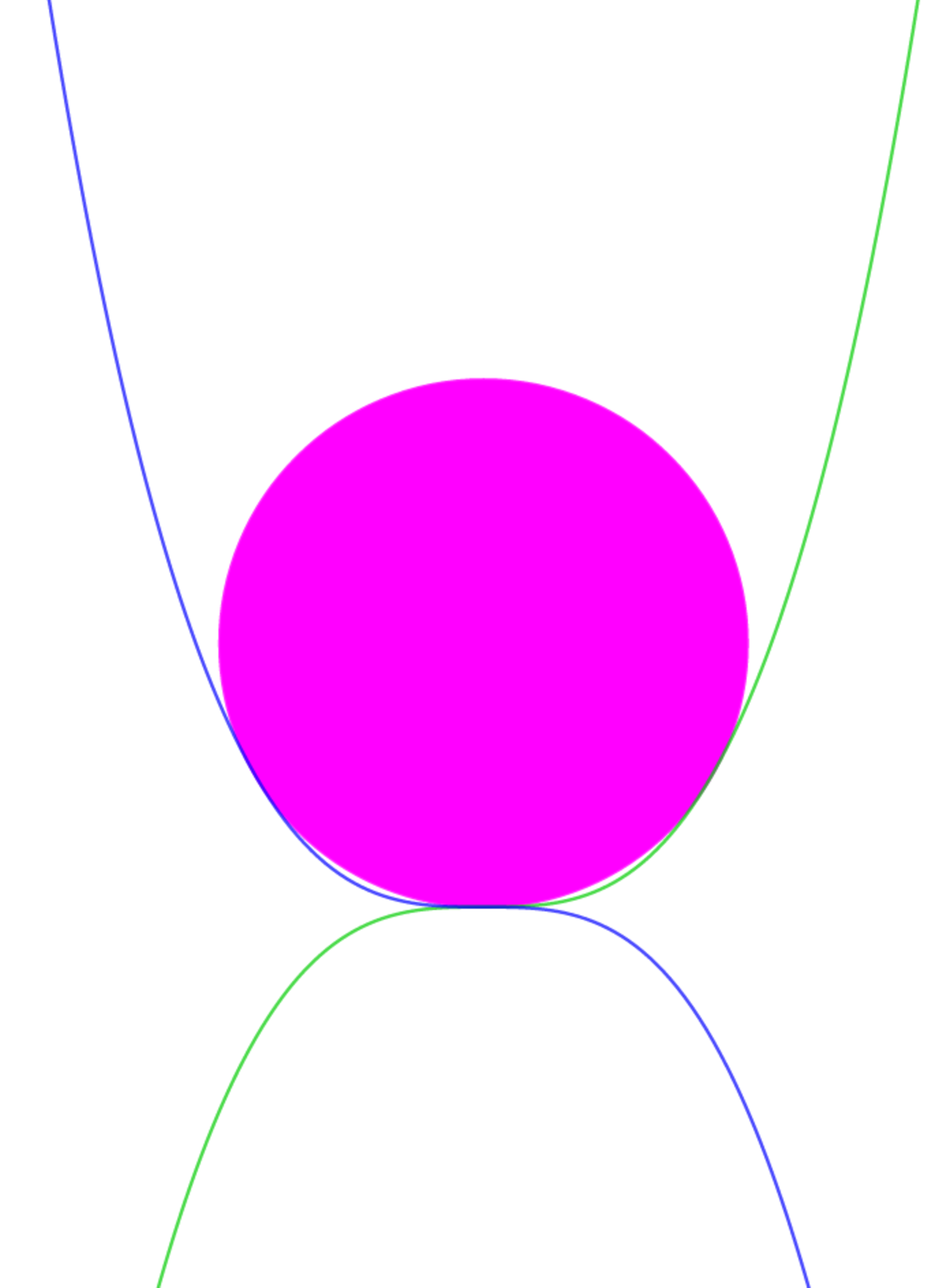
The diagram shows a green curve with equation y = x 3 and a blue curve with equation y = − x 3 - We inscribe the smallest possible circle between the curves so that the circle is just tangent to the two curves.
- Question : The area of this circle can be expressed as b a π where a and b are coprime positive integers.
-
Evaluate
a
+
b
The answer is 31.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
- The smallest possible circle will be tangent to the intersecting point between the curves y = x 3 and y = − x 3 , this point is the origin O ( 0 ; 0 ) .
- P ( 0 ; y P ) is the center of the circle, then its radius is y P
- The equation of the circle is : x ² + ( y − y P ) ² − y P ² = 0
- Since there is common point between x ² + ( y − y P ) ² − y P ² = 0 and y = x 3 , we can substitute y with x ² :
- x ² + ( x ² − y P ) ² − y P ² = 0 < = > x 2 + x 6 − 2 ⋅ y P ⋅ x 3 = 0 < = > x 4 − 2 x y P + 1 = 0
- The discriminant of this quartic equation needs to be equal to zero since there is tangency between the circle and the curve.
- Δ = − 4 3 2 y P 4 + 2 5 6 = 0 < = > y P = 3 4 3 2
- Then the area of the circle is 2 7 4 π
- a + b = 4 + 2 7 = 3 1
It's not obvious that the circle shall touch the origin as you've stated.
Let's take a calculus approach to Valentin's solution. If x 2 + ( y − r ) 2 = r 2 be tangent to the symmetric curves y = x 3 and y = − x 3 at the points ( 0 , 0 ) ; ( x 0 , x 0 3 ) ; ( − x 0 , x 0 3 ) , then WLOG the right-hand branch satisfies:
x 2 + ( x 3 − r ) 2 = r 2 ⇒ x 2 + x 6 − 2 r x 3 + r 2 = r 2 ⇒ r ( x ) = 2 x 3 + 2 x 1 .
The first derivative equal to zero yields:
r ′ ( x ) = 0 ⇒ 2 3 x 2 − 2 x 2 1 = 0 ⇒ x = 3 1 / 4 1 ;
and the second derivative at this critical point yields:
r ′ ′ ( x ) = 3 x + x 3 1 ⇒ r ( 3 1 / 4 1 ) > 0 (hence a global minimum).
NOTE: By y − axis symmetry, x = − 3 1 / 4 1 is the critical point for the left-hand branch. Thus, the area of this minimal circle computes to π ⋅ [ r ( 3 1 / 4 1 ) ] 2 = 2 7 4 π
Thanks for posting !
Log in to reply
My pleasure, Valentin.....good problem to post!
Log in to reply
I'm glad you liked it, I'm posting a new series of 100 problems : Dynamic geometry, I hope you'll enjoy it !
Log in to reply
@Valentin Duringer – Yup, I've already blown through the first half-dozen of those Dynamic Geom. probs.....locus/parametric problems are always a fun puzzle for rainy Seattle USA days!
Log in to reply
@Tom Engelsman – Ok I see... Starting te post more then...