R-L-C oscillations, not L-C oscillations.

Let the charge on the capacitor at any instant be q, the current i.

Using Kirchoff's voltage law across the circuit we get,

$L\dfrac{di}{dt} + iR + \dfrac{q}{C}= 0$
Let $U_{L}, U_{C}$ be the magnetic energy stored in the inductor and electric energy in the capacitor respectively.
$U_{L} = \dfrac{Li^{2}}{2}$
$U_{C} = \dfrac{Q^{2}}{2C}$
$\dfrac{U_{L}}{U_{C}} = LC \times \left(\dfrac{i}{q}\right)^{2}$
Coming back to the differential equation,
$L\dfrac{di}{dt} + iR + \dfrac{q}{C}= 0$
When current is maximum, $\dfrac{di}{dt} = 0$
$0 + iR = -\dfrac{q}{c}$
$\dfrac{i}{q} = -\dfrac{1}{RC}$
$\therefore \dfrac{U_{L}}{U_{C}} = LC \times \left(\dfrac{1}{RC}\right)^{2} = \dfrac{L}{R^{2}C}$
Comparing, $\alpha = \beta = \psi =1, \gamma = 2$
$\alpha + \beta + \gamma + \psi = 5$

Consider the circuit as shown in the figure below:

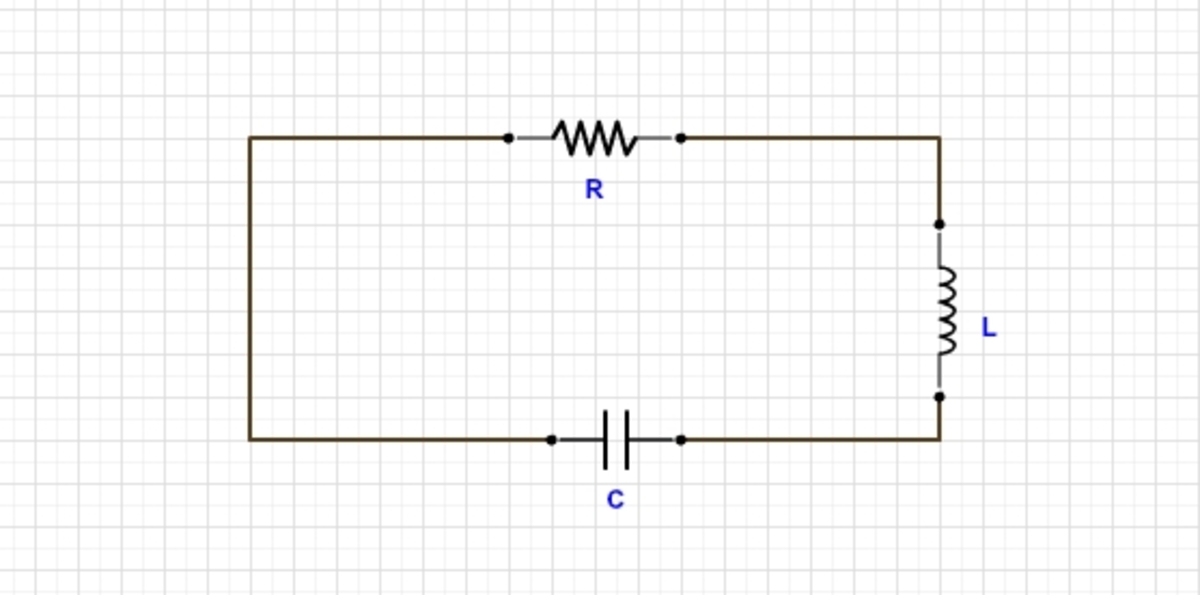
In case of an ordinary L-C circuit, the oscillations are not restricted by anything, and so the angular velocity of the circuit stays at ${\omega}_{o} = \frac {1} {\sqrt{LC}}$ , but in our case, since there is an external resistance attached, hence, there will be a loss of energy and so, the circuit would act as a damped oscillator.

Now, using the Kirchoff's voltage law , the sum of voltages across all the 3 components should be $0$ . So,

$\dfrac {q} {C} + L \dfrac {dI} {dt} + RI = 0$

where $q$ is the charge on the capacitor plates at any instant and $I$ is the current through the circuit at any instant.

Now, substituting $I=-\dfrac{dq}{dt}$ , we get a differential equation in $q$ that can be written as:

$\dfrac{{d}^{2}q} {d{t}^{2}} + \dfrac {dq}{dt} \dfrac{R}{L} -\dfrac {q}{LC} = 0$

The solution to this differential equation is identical to the solution of the differential equation for a damped SHM, which is:

$q = {q}_{o} {e}^{-\delta t} \cos{\omega t}$

where $\delta = \frac {R} {2L}$ and $\omega = \sqrt {{{\omega}_{o}}^{2} - {\delta}^{2}}$

After we have calculated the time dependence for $q$ , we can get the same for the current $I$ , by just differentiating the expression, which gives us:

$I = {q}_{o} {e}^{-\delta t} (\omega \sin{\omega t} + \delta \cos{\omega t})$

Now, the question asks for the time at which $I$ attains it's maximum value, which can be calculated by differentiating $I$ and equating it to $0$ .

$\dfrac {dI} {dt} = -{q}_{o} {e}^{-\delta t} (({\delta}^{2} - {\omega}^{2}) \cos{\omega t} + (2 \delta \omega) \sin{\omega t}) = 0$

Solving this, we get $\tan{\omega t} = \dfrac {{\omega}^{2} - {\delta}^{2}} {2\delta \omega}$ .

So, the question asks for the ratio of energy in the inductor at this instant to the ratio of energy in the capacitor at this instant, i.e.

$\dfrac {{E}_{L}} {{E}_{C}} = \dfrac {\dfrac {L{I}^{2}} {2}} {\dfrac {{q}^{2}} {2C}}$

Now, putting

• $I = -{q}_{o} {e}^{-\delta t} (\omega \sin{\omega t} + \delta \cos{\omega t})$
• $q = {q}_{o} {e}^{-\delta t} \cos{\omega t}$
• $\cos {\omega t} = \dfrac {2\delta \omega} {{\delta}^{2} + {\omega}^{2}}$
• $\sin {\omega t} = \dfrac {{\omega}^{2} - {\delta}^{2}} {{\delta}^{2} + {\omega}^{2}}$

and using the definitions of $\delta$ and $\omega$ , we get:

$\dfrac {{E}_{L}} {{E}_{C}} = \dfrac {L} {C{R}^{2}}$

Phew! So, $\psi = 1$ , $\alpha = 1$ , $\beta = 1$ and $\gamma = 2$ , giving us the answer as $5$ .

....and we're done! :)

So if we consider the series connection,

$V_{c}+V_{r}+V_{l} = 0$

$V_{c}+IR+L\dfrac{dI}{dt} = 0$

Now for maximum current,

$\dfrac{dI}{dt} = 0$

So, $V_{c}+IR= 0$

$\therefore V_{c}=-IR$

So ratio of energy,

$Ratio = \dfrac{\dfrac{1}{2}LI^2}{\dfrac{1}{2}CV_{c}^2}$

$= \dfrac{\dfrac{1}{2}LI^2}{\dfrac{1}{2}CI^2R^2}$

$=\dfrac{L}{CR^2}$

So, Ans is $1+1+1+2=\boxed{5}$