Race on tracks

The long bottom section of track B at a lower level than that of track A. So the ball B loses more potential energy while getting to it, gaining in the process more kinetic energy and therefore higher speed. This translates into shorter time to traverse the track.

This is not a solution!

I think this video by 3b1b is pretty much relevant to this question.

In track B the depth of the track is more than that of A. Hence, when the ball is rolling on track B it will have more potential energy stored than when it is rolling on track A. By conservation of energy we know that all potential energy stored is transformed into kinetic energy which means more the potential energy the body store's more is the velocity and faster the ball will move. Therefore the ball will reach the other end more faster in track B.

This 4 second video shows that as Ball B on the dipped track goes steeply down its horizontal velocity increases, so it gets ahead. Even though it slows down again to the speed of the other ball as the tracks even out, Ball B stays ahead, and wins the race.

I initially got this wrong, and was having trouble reconciling the solutions given; so I decided to write my own solution.

Figure 1. shows a simplified side profile of the given tracks A and B ( A is Black and B is Red ). I begin my analysis at the position marked "0" in Figure 1.

At this point both balls have the same velocity (in the x direction), $V$ . From here lets compare the x components of their velocity as the balls traverse the distance $D$ from point 0 to point 3.

$\displaystyle{\underline{\text{Ball A, 0-3}}}$

From position 0 to 3 the velocity of ball a will remain unchanged. Namely $V_0$

$\displaystyle{\underline{\text{Ball B, 0-1}}}$

Figure 2. shows the forces acting on the ball relative to the common frame of reference between track A and B.

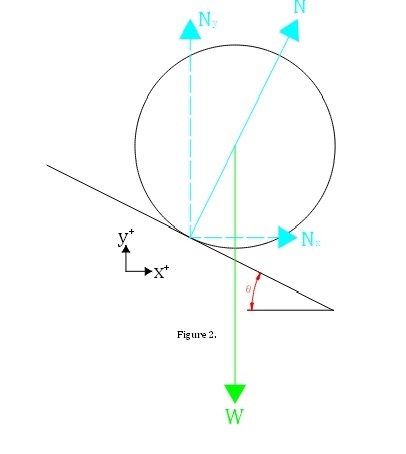
Summing the forces in the x direction we obtain. $\displaystyle \sum{F_x} = N\sin\theta = ma_x$ from this we can see $a_x = \frac{N}{m}\sin\theta > 0$ for all $0<\theta<\frac{\pi}{2}$

As the ball traverses from point 0 to 1, it will undergo an acceleration in the x direction and as a consequence its component of velocity in the x direction will increase beyond that of $V_0$ . We can say for simplicity that the average component of velocity in the x direction between 0 and 1 is greater than $V_0$ or $\overline{V}_{0-1} > V_0$

$\displaystyle{\underline{\text{Ball B, 1-2}}}$

At point 1 Ball B's $a_x \rightarrow 0$ and the x component of its velocity will remain constant ( what it had obtained at the bottom of the incline) until it moves to point 2. Thus $V_{1-2} > V_0$ for the duration of the interval 1-2.

$\displaystyle{\underline{\text{Ball B, 2-3}}}$

Ball B will undergo a mirror acceleration ( -x direction) from that of interval 0-1. Its x component of velocity will decrease from $V_{1-2} \text{ to } V_0$ between point 2 and 3, meaning $\overline{V}_{2-3} > V_0$ over the interval 2-3.

Figure 3. is representative of the velocities of the balls as they traverse from 0-3.

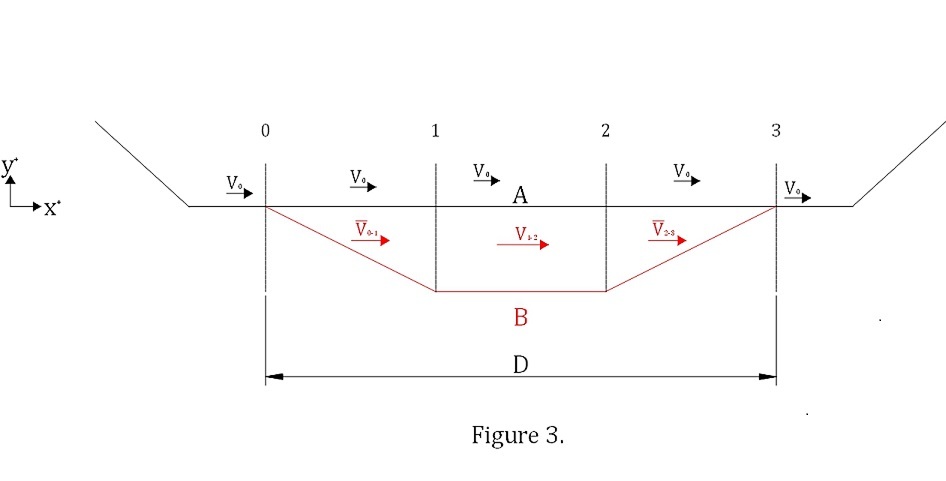
As a result the average x component of velocity of Ball B is larger in every interval over the distance $D$ , thus it will arrive at point 3 before Ball A.

We see that for for A the ball will go almost in same velocity but for B first the speed will be almost as same as A but then it will increase as it goes down , but then the ball have to go opposite to gravity but the effective velocity is more than ball in A and so the ball in B will reach first. There is also a nice mathematical point of view https://drive.google.com/file/d/11ca-5FO_tgH2wXMg2at1qemCMukqmAN0/view?usp=drivesdk This is the solution of a more generalized problem (same problem) proposed by John Bernoulli (if you like I can give that also)

There is a problem in variational calculus called brachistrone problem which is similar to this problem

It appears as though both tracks are slightly declining from left to right. This is only a presumption coming from someone with no more than rudimentary understanding of physics, and the main reason I'm posting this comment is with the hope that someone will either correct me or point something new out to me.

Anyway, since both tracks are declining, then the first steep ascending slope on track b will be greater than the second descending slope, which would result in a positive increase in speed and an overall shorter account of time to get from point a to be when compared to track a. Whereas if the tracks were on level surfaces, then the two steeper slopes on track b would cancel each other out and thus both track a and track b would take the same amount of time (also if they were on level surfaces then neither would complete the whole track, correct?)

I got it right, but I do not think it is necessary the right solution. If the mass of the ball is low or the gravity is low then the speed increase would not compensate the longer distance.

If the track was perfectly flat, the ball does not move. If it is only a touch depressed in the center it would do the distance very slowly. So the more depressed clearly the faster the ball goes

Suppose the initial down ramps and the final up ramps (which are identical for tracks A and B) are shrunk to zero. Then the ball on track A never gets going at all, and never gets to the other end! But ball B can roll down the slope, along the bottom, climb up the far slope and compete the journey, thus beating A by a country mile.

Once you have this insight it easy to intuit the correct solution.

Basically, imagine you’re on a bike on track A, you will have one speed boost going down and go the full length getting you back up the hill. Then, imagine you’re on the same bike, but on Track B and now instead of one speed boost (potential energy), you get two boosts due to a greater drop (potential energy) but gaining more speed (kinetic energy) bringing you up the hills quicker than just one speed boost of track A.