Race Probability!

We calculate the probability that B will win. For B to win, A's and B's times both need to be between $11$ and $12$ seconds and B's time needs to be lower than A's.

• The probability that A's time is between $11$ and $12$ seconds is $\dfrac{1}{2}$

• The probability that B's time is between $11$ and $12$ seconds is $\dfrac{1}{2}$

• Given that A's and B's times are both between $11$ and $12$ seconds, the probability that B's time is lower than A's is $\dfrac{1}{2}$ (since both runners' times are uniformly distributed)

Thus the probability that B wins the race is $\left( \dfrac{1}{2} \right) \left( \dfrac{1}{2} \right) \left( \dfrac{1}{2} \right) = \dfrac{1}{8}$ , therefore the probability that B loses, and thus Adam wins, the race is $\ \boxed{\dfrac{7}{8}}$

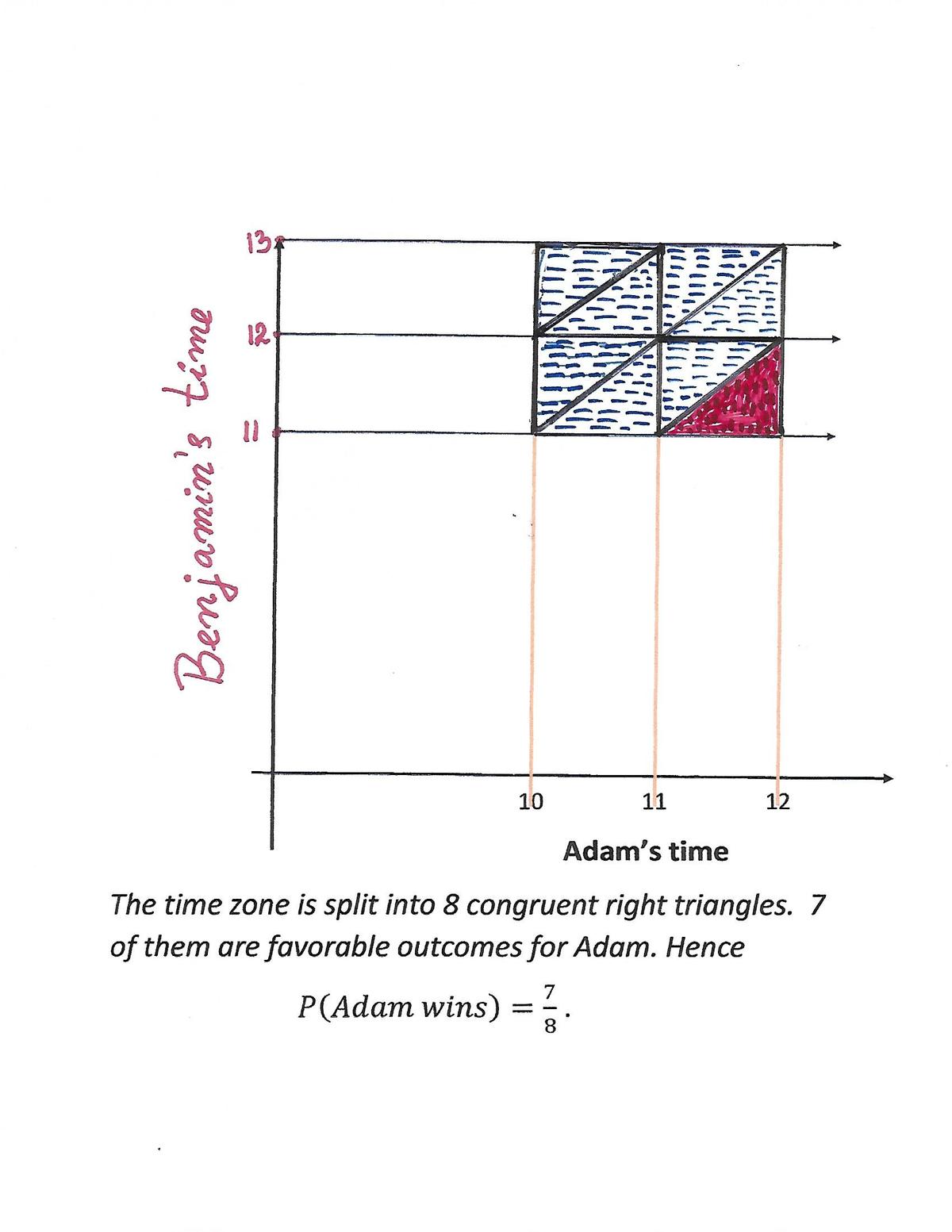
We can illustrate this graphically, and since we have 2 different people to consider, we can use Area to work out the probability. Let Adam's time be $x$ and Benjamin's time be $y$ . On the graph shown below, we can see that the region encompassed within the first 4 lines is the total outcomes (a square). Also, for Adam to win, $x < y$ so it also has to be above the purple line $y = x$ . We can clearly see that the proportion of the area in the cases that Adam wins is $\frac78$

Let $t_A$ be the time Adam takes to run the race. Likewise $t_B$ is the time Benjamin takes to run the race.

If $10 < t_A < 11$ Adam wins. This happens with possibility $\frac{1}{2}$ .

For $11 < t_A < 12$ , fix $t_A$ . Then the possibility $P(t_A < t_B) = \frac{1}{2} (13 - t_A)$ . Integration over all $t_A \in [11,12]$ gives: $\int_{11}^{12} \frac{1}{2}(13 - t_A) dt_A = \frac{1}{2} {\left[13 t_A - \frac{1}{2} t_A^2\right]}_{11}^{12} = \frac{3}{4}$

Hence the total possibility Adam wins is: $\frac{1}{2} \cdot 1 + \frac{1}{2} \cdot \frac{3}{4} = \frac{7}{8}$

Here's a visual representation of what happens:

We simulate lots of races, the red dot represents Adam, the blue one represents Benjamin. The lines on the right show who won that specific race and there are overall statistics at the bottom. We can see, that the ratio is really close to $\frac{7}{8}$ which is $0.875$ .

I realize this is not a complete solution, but only a simulation using programming.

(Here's another picture with much more races and without the connecting lines):

We can just think through this logically. The total probability that A will win is the sum of all probabilities in all scenarios where A wins. By my count, there are 3 such scenarios.

Scenario 1 : $t_A < 11s$ . A can have a time less than 11 seconds and it is impossible for B to win. This will happen exactly 1/2 of the time. This is because all of the times for both runners are evenly distributed and continuous, so half of the time A will be faster than B.

Scenario 2 : $12s \geq t_A \geq 11s$ & $t_B > 12s$ . $12s \geq t_A \geq 11s$ happens 1/2 of the time. However, $t_B > 12s$ also happens 1/2 of the time. So the probability of this scenario happening is 1/2 * 1/2 = 1/4.

Scenario 3 : $12s \geq t_A \geq 11s$ & $12s \geq t_B \geq 11s$ . Once again, we see that this scenario will only happen 1/4 of the time. However, this condition doesn't guarantee either runner a win. We need to additionally ask, what is the probability that A and B pick a time between 11s and 12s and $t_A < t_B$ . I'm going to impose a condition that I've been secretly doing this whole time: $P( t_A = t_B) = 0.$ Why can I do this? Well, this question is no different from asking 2 people to pick a real number from 0 to 1 inclusive and asking what the probability is that they both pick exactly the same number. It might be possible, but the probability is technically zero. There are infinite numbers to choose from for both people, and it is so exceedingly unlikely that they choose the same exact number that we say the probability is zero. So now, what is the probability that $t_A < t_B$ in this scenario? 1/2 of course! Again, it's like just picking 2 numbers from 0 to 1 on the number line at random and asking the probability that the first number will be smaller. Since either case is equally likely (by symmetry) and we have imposed that picking the same number isn't allowed there are only 2 possible outcomes. So in this third scenario (which occurs with 1/4 probability), there's a 1/2 probability that $t_A < t_B$ .

So adding it all up we get, $P(t_A < t_B) = P(Scenario 1) + P(Scenario 2) + \frac{1}{2} P(Scenario 3) = \frac{1}{2} + \frac{1}{4} + \frac{1}{2}\frac{1}{4} = \frac{7}{8}$

I know this was extremely wordy, but that was my full thought process for this problem.

Here’s a programming solution to the problem:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

import random;
def randrangedec(min, max, step):
    mult = 1;
    while(step < 1):
        step *= 10;
        mult *= 10;
    num = random.randrange(min * mult, max * mult, step);
    return num / mult;

count = 0;
step = 0.00001;
iterations = 2999999;
for x in range(0, iterations):
    if(randrangedec(10, 12, step) < randrangedec(11, 13, step)):
        count += 1;
print(count / iterations);

Comment: the question said Adam's times were 10-12 seconds and Benjamin's were 11-13. It asked what portion of the times Adam wins. The answers ran from 1/2 - 7/8. None of the answers were correct. Benjamin wins 7/8 races NOT Adam.

Solution: There are four basic cases:

Adam 10-11 Benjamin 11-12, Benjamin wins

Adam 10-11 Benjamin 12-13, Benjamin wins

Adam 11-12 Benjamin 11-12, Either could win

Adam 11-12 Benjamin 12-13, Benjamin wins

So, Benjamin is guaranteed to win 3 of 4 races. Because of the uniform distribution, there is an equal chance that either wins the other 1 of 4 races: 1/2 go to Adam and 1/2 to Benjamin, giving 1 of 8 races to each.

Therefore Benjamin wins 7 out of 8 races, and Adam wins 1 out of 8.

The random variable of interest is the difference between finish times. A difference is the same as a sum but negating one of the terms. The probability density function (pdf) of two independent random variables is the convolution of the two pdfs. Thus the difference in finishing times (Adam minus Ben) is the convolution of uniform(10, 12) with uniform(-13,-11). The convolution of two rectangle signals is a triangle. So the pdf will be an isosceles triangle whose base is from the minimum (10-13=-3) to the maximum (12-11=1). The height of the triangle will be maximum when the two rectangles are perfectly aligned, in which case the product of the two rectangles will be (1/2)(1/2)=1/4 times their width of 2 equals 1/2, and this is the peak of the triangle. As expected the total area of the triangle is 1 (two half triangles of area (1/2)(2)(1/2)). Adam wins whenever the convolved random variable is less than zero, which is the interval from -3 to 0. The part of the triangle where Ben wins is the interval 0 to 1. At t=0, the triangle is half way down from its peak of 1/2 and has a height of 1/4. The probability of Ben winning is therefore the area of this 0 to 1 triangle with base=1 and height=1/4. This area is 1/8. Adam wins in all other cases, which means he wins 7/8 of the time.

• Adam has A : a 50% chance of winning 100% of the time, no matter how fast Benjamin runs.
• Adam has B : a 50% chance of winning 75% of the time, depending on Benjamins performance*.

This means Adams chance of winning (W) is W = A + B

• W = (50% * 100%) + (50% * 75%)
• W = ( $\frac{1}{2}$ * 1) + ( $\frac{1}{2}$ * $\frac{3}{4}$ )
• W = ( $\frac{4}{8}$ ) + ( $\frac{3}{8}$ )

• W = $\frac{7}{8}$ = 87.5%

• Benjamins performance can be a 50% chance of winning 25% of the time and a 50% chance of winning 0% of the time.