Rainbow TaiChi
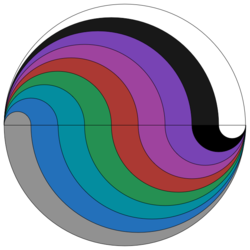The above is a circle of radius 9. It has been cut up into 9 different regions, using semicircles of integer radius.
The area of the largest region can be written as A π . What is A ?
The answer is 9.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
How do you show that every region is the same?
I guess you mean that they have the same area, as opposed to that they are the same shape.
Log in to reply
Sure. Notice that the semicircles have cut the diameter into 9 equal parts.
For example, the area of the G r e e n region is:- ( 2 π × 4 2 − 2 π × 3 2 ) + ( 2 π × 6 2 − 2 π × 5 2 ) = 9 π
And for the rest of the region it can be shown in a similar way. In fact,
( 2 π × n 2 − 2 π × ( n − 1 ) 2 ) + ( 2 π × ( 9 − n + 1 ) 2 − 2 π × ( 9 − n ) 2 ) = 9 π
Log in to reply
To calculate the area of green region you have taken r a d i u s = 4 , how could that be.... it is the diameter, right?
Log in to reply
@Anandhu Raj – Check again anandhu
Log in to reply
@Shourya Pandey – Oops...didn't read the question correctly...Thought 9 cm was diameter of big circle :(
The area of every region is the same and i.e. 9π
All regions have equal areas, hence (pi.r^2)/9=81pi/9=9pi, A=9
Nice solution
How do you prove that the area is the same for all sections? Is there a geometric process?
The area of every region is the same. Thus area of the largest region is 9 π × 9 2 = 9 π .
∴ A = 9