Roots To The 9th!

Algebra Level 3

If α , β , γ \alpha , \beta , \gamma are roots of the equation x 3 + 3 x + 9 = 0 , x^{3} + 3x + 9 = 0, find the value of α 9 + β 9 + γ 9 . \alpha^{9} + \beta^9 + \gamma^{9}.


The answer is 0.

View wiki
Ayush Parasar by Ayush Parasar , 22, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

By Vieta's formulas we know that: α + β + γ = 0 \alpha+\beta+\gamma=0 , α β + α γ + β γ = 3 \alpha \beta+\alpha \gamma + \beta\gamma=3 and α β γ = − 9 \alpha \beta \gamma=-9 .

The fast way

Note that x 3 = − 3 ( x + 3 ) x^3=-3(x+3) , so x 9 = − 27 ( x 3 + 9 x 2 + 27 x + 27 ) x^9=-27(x^3+9x^2+27x+27) . Hence, the value we want is:

α 9 + β 9 + γ 9 = − 27 ( ( α 3 + β 3 + γ 3 ) + 9 ( α 2 + β 2 + γ 2 ) + 27 ( α + β + γ ) + 81 ) \alpha^9+\beta^9+\gamma^9=-27((\alpha^3+\beta^3+\gamma^3)+9(\alpha^2+\beta^2+\gamma^2)+27(\alpha+\beta+\gamma)+81)

α 2 + β 2 + γ 2 = ( α + β + γ ) 2 − 2 ( α β + α γ + β γ ) \alpha^2+\beta^2+\gamma^2=(\alpha + \beta + \gamma)^2-2(\alpha \beta+\alpha \gamma + \beta\gamma)

α 2 + β 2 + γ 2 = ( 0 ) 2 − 2 ( 3 ) = − 6 \alpha^2+\beta^2+\gamma^2=(0)^2-2(3)=-6

α 3 + β 3 + γ 3 = ( α + β + γ ) 3 − 3 ( α + β + γ ) ( α β + α γ + β γ ) + 3 ( α β γ ) \alpha^3+\beta^3+\gamma^3=(\alpha+\beta+\gamma)^3-3(\alpha+\beta+\gamma)(\alpha \beta+\alpha \gamma + \beta\gamma)+3(\alpha \beta \gamma)

α 3 + β 3 + γ 3 = ( 0 ) 3 − 3 ( 0 ) ( 3 ) + 3 ( − 9 ) = − 27 \alpha^3+\beta^3+\gamma^3=(0)^3-3(0)(3)+3(-9)=-27

α 9 + β 9 + γ 9 = − 27 ( − 27 + 9 ( − 6 ) + 27 ( 0 ) + 81 ) \alpha^9+\beta^9+\gamma^9=-27(-27+9(-6)+27(0)+81)

α 9 + β 9 + γ 9 = 0 \alpha^9+\beta^9+\gamma^9=\boxed{0}

The long way

By the identity:

α 3 + β 3 + γ 3 = ( α + β + γ ) 3 − 3 ( α + β + γ ) ( α β + α γ + β γ ) + 3 ( α β γ ) \alpha^3+\beta^3+\gamma^3=(\alpha+\beta+\gamma)^3-3(\alpha+\beta+\gamma)(\alpha \beta+\alpha \gamma + \beta\gamma)+3(\alpha \beta \gamma)

α 3 + β 3 + γ 3 = ( 0 ) 3 − 3 ( 0 ) ( 3 ) + 3 ( − 9 ) = − 27 \alpha^3+\beta^3+\gamma^3=(0)^3-3(0)(3)+3(-9)=-27

Similarly:

α 9 + β 9 + γ 9 = ( α 3 + β 3 + γ 3 ) 3 − 3 ( α 3 + β 3 + γ 3 ) ( ( α β ) 3 + ( α γ ) 3 + ( β γ ) 3 ) + 3 ( α β γ ) 3 \alpha^9+\beta^9+\gamma^9=(\alpha^3+\beta^3+\gamma^3)^3-3(\alpha^3+\beta^3+\gamma^3)((\alpha \beta)^3+(\alpha \gamma)^3+(\beta \gamma)^3)+3(\alpha \beta \gamma)^3

Again, in a similar way:

( α β ) 3 + ( α γ ) 3 + ( β γ ) 3 = ( α β + α γ + β γ ) 3 − 3 α β γ ( α β + α γ + β γ ) ( α + β + γ ) + 3 ( α β γ ) 2 (\alpha \beta)^3+(\alpha \gamma)^3+(\beta \gamma)^3=(\alpha\beta+\alpha\gamma+\beta\gamma)^3-3\alpha\beta\gamma(\alpha\beta+\alpha\gamma+\beta\gamma)(\alpha+\beta+\gamma)+3(\alpha\beta\gamma)^2

So,

α 9 + β 9 + γ 9 = ( α 3 + β 3 + γ 3 ) 3 − 3 ( α 3 + β 3 + γ 3 ) ( ( α β + α γ + β γ ) 3 − 3 α β γ ( α β + α γ + β γ ) ( α + β + γ ) + 3 ( α β γ ) 2 ) + 3 ( α β γ ) 3 \alpha^9+\beta^9+\gamma^9=(\alpha^3+\beta^3+\gamma^3)^3-3(\alpha^3+\beta^3+\gamma^3)((\alpha\beta+\alpha\gamma+\beta\gamma)^3-3\alpha\beta\gamma(\alpha\beta+\alpha\gamma+\beta\gamma)(\alpha+\beta+\gamma)+3(\alpha\beta\gamma)^2)+3(\alpha \beta \gamma)^3

Substituting the known values we arrive to:

α 9 + β 9 + γ 9 = ( − 27 ) 3 − 3 ( − 27 ) ( ( 3 ) 3 − 3 ( − 9 ) ( 6 ) ( 0 ) + 3 ( − 9 ) 2 ) + 3 ( − 9 ) 3 \alpha^9+\beta^9+\gamma^9=(-27)^3-3(-27)((3)^3-3(-9)(6)(0)+3(-9)^2)+3(-9)^3

α 9 + β 9 + γ 9 = 0 \alpha^9+\beta^9+\gamma^9=\boxed{0}

We can also do this by Newton's Sums, but since 3 2 = 9 3^2=9 , these are faster ways.

36 Helpful 0 Interesting 0 Brilliant 1 Confused

Note: In the fast way, you could use α 3 = − 3 α − 9 \alpha^3 = - 3 \alpha - 9 , and hence ∑ α 3 = − 27 − 3 ∑ α = − 27 \sum \alpha^3 = -27 - 3 \sum \alpha = - 27 .

Calvin Lin Staff - 6 years, 5 months ago

Log in to reply

Another way to make it a bit shorter is to substitute x 3 x^{3} into the expansion of ( − 3 x − 9 ) 3 (-3x-9)^{3} to give -81( 3 x 2 x^{2} +8 x {x} +6). From there we calculate 3 x 2 x^{2} = α 2 \alpha^{2} + β 2 \beta^{2} + γ 2 \gamma^{2} = -6, 8 x {x} = 0, such that the expression = 0

Curtis Clement - 6 years, 5 months ago

Oh yes, a faster way :D

Alan Enrique Ontiveros Salazar - 6 years, 5 months ago

Much faster way , learnt in Adity raut's note - Bashing Unavailable

t n = t n − 1 + 1 2 t n − 2 + 1 6 t n − 3 t_{n} = t_{n-1} + \dfrac{1}{2}t_{n - 2} + \dfrac{1}{6}t_{n-3} ( t n = a n + b n + c n t_{n} = a^n + b^n + c^n )

Now α = a , β = b , γ = c \alpha =a , \beta=b , \gamma=c

B y V i e t a , a + b + c = 0 ~By ~Vieta~, a + b + c = 0

Applying the general term above ,

a 2 + b 2 + c 2 = 0 a^2 + b^2 + c^2 = 0 , this implies t 3 = 0 t_{3} = 0 and successive quadratics are dependent on the preceding , thus each is zero!

U Z - 6 years, 5 months ago

Log in to reply

@megh choksi You are referring to Newton's Identity, You have to generate the recurrence for each polynomial. The actual recurrence relation is:

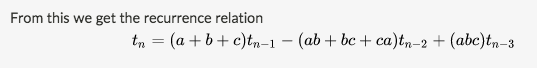
The one that you stated is the recurrence relation for Aditya's example, and does not hold for this problem.

Note also that t 0 = 3 ≠ 0 t_0 = 3 \neq 0 . t 3 = − 27 ≠ 0 t_3 = -27 \neq 0 . If each of the powers have a sum of 0, then the variables must all be 0.

Calvin Lin Staff - 6 years, 5 months ago

Log in to reply

@Calvin Lin – Oh thanks , I did the same mistake in another problem too

U Z - 6 years, 5 months ago

writing ∑ α \sum \alpha means cyclic i.e α + β + γ = 0 \alpha + \beta + \gamma = 0 so it gives -27

U Z - 6 years, 5 months ago

Exactly what I did !! Look at my solution.

Akshat Sharda - 5 years, 6 months ago
Chew-Seong Cheong
Dec 26, 2014

The problem can be solved using Newton's Sums method.

Let S 1 = α + β + γ = 0 S_1 = \alpha + \beta + \gamma = 0 , S 2 = α β + β γ + γ α = 3 S_2 = \alpha\beta + \beta \gamma + \gamma\alpha = 3 and S 3 = α β γ = − 9 S_3 = \alpha\beta\gamma = -9 ; then P n = α n + β n + γ n P_n = \alpha^n + \beta^n + \gamma^n , where n = 1 , 2 , 3... n = 1,2,3... is given by:

{ P 1 = S 1 = 0 P 2 = S 1 P 1 − 2 S 2 = 0 − 2 ( 3 ) = − 6 P 3 = S 1 P 2 − S 2 P 1 + 3 S 3 = 0 − 0 + 3 ( − 9 ) = − 27 P 4 = S 1 P 3 − S 2 P 2 + S 3 P 1 = 0 − 3 ( − 6 ) + 0 = 18 P 5 = S 1 P 4 − S 2 P 3 + S 3 P 2 = 0 − 3 ( − 27 ) − 9 ( 6 ) = 135 P 6 = S 1 P 5 − S 2 P 4 + S 3 P 3 = 0 − 3 ( 18 ) − 9 ( − 27 ) = 189 P 7 = S 1 P 6 − S 2 P 5 + S 3 P 4 = 0 − 3 ( 135 ) − 9 ( 18 ) = − 567 P 8 = S 1 P 7 − S 2 P 6 + S 3 P 5 = 0 − 3 ( 189 ) − 9 ( 135 ) = − 1782 P 9 = S 1 P 8 − S 2 P 7 + S 3 P 6 = 0 − 3 ( − 567 ) − 9 ( 189 ) = 0 \begin {cases} P_1 = S_1 & & = 0 \\ P_2 = S_1 P_1 -2S_2 & = 0-2(3) & = -6 \\ P_3 = S_1 P_2-S_2P_1 + 3S_3 & = 0 - 0 +3(-9) & = -27 \\ P_4 = S_1P_3-S_2P_2 + S_3P_1 & = 0-3(-6)+0 & = 18 \\ P_5 = S_1P_4-S_2P_3 + S_3P_2 & = 0-3(-27)-9(6) & = 135 \\ P_6 = S_1P_5-S_2P_4 + S_3P_3 & = 0-3(18)-9(-27) & = 189 \\ P_7 = S_1P_6-S_2P_5 + S_3P_4 & = 0-3(135)-9(18) & = -567 \\ P_8 = S_1P_7-S_2P_6 + S_3P_5 & = 0-3(189)-9(135) & = -1782 \\ P_9 = S_1P_8-S_2P_7 + S_3P_6 & = 0-3(-567)-9(189) & = 0 \end {cases}

Therefore, P 9 = α 9 + β 9 + γ 9 = 0 P_9 = \alpha^9 + \beta^9 + \gamma^9 = \boxed{0} .

24 Helpful 1 Interesting 0 Brilliant 0 Confused
Akshat Sharda
Nov 30, 2015

x 3 + 3 x + 9 = 0 ⇒ x 3 = − 3 ( x + 3 ) x 9 = − 27 ( x 3 + 9 x 2 + 27 x + 27 ) ∑ x 9 = − 27 ( ∑ ( x 3 + 9 x 2 + 27 x + 27 ) ) = − 27 ( ∑ x 3 + 9 ∑ x 2 + 27 ∑ x + ∑ 27 ) By Newton’s Sums : ∑ x = 0 , ∑ x 2 = − 6 and ∑ x 3 = − 27 = − 27 ( − 27 + 9 ( − 6 ) + 27 ( 0 ) + 27 × 3 ) = − 27 ( 0 ) = 0 x^3+3x+9=0\Rightarrow x^3=-3(x+3) \\ x^9=-27(x^3+9x^2+27x+27) \\ \sum x^9=-27\left(\sum(x^3+9x^2+27x+27)\right) \\ =-27\left(\sum x^3+9\sum x^2+27\sum x+\sum 27\right) \\ \text{By Newton's Sums : }\sum x=0,\sum x^2=-6 \text{ and } \sum x^3=-27 \\ =-27(-27+9(-6)+27(0)+27×3) \\ =-27(0)=\boxed{0}

4 Helpful 0 Interesting 2 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...