Calculated signed sum

We can use elimination to solve this system of equations.

$x+y=55 \\ x-y=27$

Adding these equations gives:

$2x=82\implies x=\boxed{41}$

Take the first equation and rearrange making y as the subject

x + y =55

55 - x = y

Substitute in equation. 2

x - (55 - x) = 27

2x = 27 + 55

x = $\frac{82}{2}$

x = $\boxed{41}$

$x+y+x-y=55+27=82=2x$ thus $x=\frac{82}{2}=\boxed{41}$ .

55-27=28 Half of 28 =14 27+14 = 41

As we know, Max{x,y}=(|x+y|/2)+(|x-y|/2) Hence, Max{x,y}=(55+27)/2=41

In this problem, x 's role in both equations is the same, and y 's role "swings" from negative to positive. First adding y and then subtracting y is like watching a swinging pendulum with its pivot at x on a number line. The pendulum swings from 27 to 55.

Thinking about the problem this way, you can see that the distance 55 - 27 = 28 would be twice the length of the y pendulum. Therefore, y=14 . And therefore x = 27 + y = 41

If X+Y = 55 and X-Y = 27, then 55-27 = 14 or 2Y

So.. Y=14

Then.. 55-14 = 41

If x - y = 27, than x is 27 more than y. So x is larger, and y is smaller. However, now we have to calculate the actual numbers, we have 55 = x(27 + z) + y(z). So, 55 = 27 + z + z. Now, we simplify : 55 = 27 + 2z. 55 -27 = 2z. 28 = 2z. 14 = z. So, we go back, and we get 55 = x(27 + 14) + y(14). So, x is 41, and y is 14.

x + y =55 x - y =27

add +y and -y and the x

x + y =55 the y's cancel out

+x - y =27

2x =82 x=41 TADA!!!!!!

$x + y = 55$

$+ ( x - y = 27)$

$=> (x + x) + (y-y) = (55 + 27)$

$=> 2x = 82$

$=> x = 41$ (Dividing both sides by 2)

x+y=55 . . . . . (1)

x-y=27 . . . . . . (2)

adding (1) and (2) we get,

2x=82

x=41

substituting x=41 in (1) we get,

41+y=55

y=14

therefore,x is greater than y.

Answer is 41

Given that, X+y=55.....(1) X-y=27...... (2) Add equation 1 and 2 2x=82 X=41. Again, subtraction between equation 1 and 2 2y=28 Y=14.. We are compare between X and Y ...., X=41 ..is the largest numbers

x+y=55 -------(1) x-y=27 -------(2)

add (1) & (2)----- 2x=82;

then x=41. Substitute the value of 'x' in any of the two equations.

From (1) we get 41+y=55 =>y=55-41 =>y=14

So 'x' is larger. X=41.

here it is , $x+y$ = $55$ .....................(1)

and, $x -y$ = $27$ .......................(2)

adding these 2 equations, we get , 2x =82

or, x= 41....................[the larger value]

(x+y=55) +(x-y=27) 2x=82 x=41

Simply see that y is a number that if added to x gives 55 and if subtracted from x gives 27. We know therefore x is halfway between 27 and 55. We also know x is larger than y because x-y is positive.

Write a solution. Plugging in each of the solutions, the only true answer was 41.

Find out any 1's variable value put it in other equation ..then choose the greater one..

1. X + Y = 55
2. X - Y = 27
3. 55 - 27 = 14 so
4. Y = 14 which means
5. X = 41

X+Y=55... (1) X-Y=27....(2) (1)+(2).. 2X=82 X=41

(x+y=55) +

(x-y=27)

2x=82

X=82/2

X=41

Work out the difference between 55 and 27 = 28

Devide by 2 = 14

Then either add 14 to 27 = 41

Or take 14 from 55 = 41

All I did was test each one

x + y = 55

x - y = 27

x = 55 - y

x = 27 + y

(x=55-y) - (x=27+y) = (28 - 2y = 0)

2y = 28

y = 14

x = 27 + y

x = 27 + 14 = 41

x = 41 y = 14

x>y

x + y = 55 y = 55 - x

x - y = 27 x - (55 - x) = 27 x - 55 + x = 27 2x = 82 x = 41

y = 55 - 41 y = 14

x+y= 55 x=55-y x-y=27 x=27+y

since x=x

55-y=27+y solve for y y=14

x=55-y=55-14=41 x=27+y=27+14= 41

Adding both the equations we get 2x=82;thus x=41

Adding the two equations, we get $2x=82$ or $x=41$ . Substitute $x=41$ to any of the given equations to get $y=14$ .

$\color{#D61F06}\large \boxed{answer=41}$

I actually do not understand with what you meant with : ...,find the larger of... What do you mean with the word "larger" in your question actually? Are you asking which value between x or y is larger? Thank you.

Just add both of the sums then average to find the answer 55 + 27 = 82 82/2 = 41

Find the difference between the two number values which is 28. Divide by two, 14 subtract from or add to the number values = 41

3/4 + 1/4 = 1 3/4 - 1/4 = 1/2 Adjust proportions as above... the answer is halfway between the two values!

Imagine x is your base. That means x is directly in between 55 and 27 because you are only changing x's value by y. The difference between 55 and 27 is 28. From here either count down 14 from 55 or count up 14 from 27. The answer is 41.

Add both equations We the equilibrium equation as 2x=82.From this x=41 Substitute x value in first or second equation, We get y=14

Subtract them from each other and 2y equals 30

Or, just find the mid point between 55 and 27. 55-27=28, 28/2=14, 27+14=41. Only works with this problem because Y is being added in one and subtracted in the second. Bit more problem solving route then algebra :)

x = 27 + y 27 + y + y = 55 27 + 2y = 55 2y = 28 y = 14 x + 14 = 55 x = 41

55-27=28 28/2=14 27+14=41 Check work 55-14=41 y=14 x=41

The greater is 41

This method is question-specific to solve the problem without writing, using simple math you can do in your head.

here, adding two equation we get

x-y = 27

(-)x+(-)y = (-) 55 multipling minus to equation 2nd

-2y= -28 y= 14 ,put this value of y in equation 1st

x-14= 27 x= 41

X= 41 Y = 14 in which greater is x's value so answer is 41...

X+Y=55

X-Y=27

2X=82 X=41

$x+y = 55$ , $x-y = 27$

-You can also add the equations, but I chose to subtract the first equation from the second, in order to eliminate $x$ $x+y = 55$ - $x-y = 27$ = $2y$ = $28$ $y$ = $14$ -I immediately knew then that $x$ had to be the variable with the larger value since 14 is less than half of 55. Now, all I had to do was to substitute the $y$ value into the first equation. So....

$x + 14 = 55$ $x = 55 - 14$ $x = 41$

The final answer is 41.....

x+y=55 x-y=27

Subtract the bottom equation from the top to get: 2x= 28

Meaning: x=14

55-14=y

Y=41

This problem is a mere beginner.

                x+y=55
                x -y=27

by adding both equations we get,

                2x=82

  so, x=41
        y=14

And, x>y

First of all I found the difference between 55 and 27 (28).

Given that x was positive throughout the only difference between the equations was 2y.

Given this

2y=28

y=14

55-14=41

Since the same number is both added and subtracted from x, x must equal the number in the exact middle of the solutions. In other words, x is the average.

55 + 27 = 82

82 / 2 = 41

A long way of doing it, but requires less mathematical skills is substite each number in.

55-41=14, 14+27=41, therefore 41 will satisfy the equation. You can try these with the other three numbers and you will get; 55=31, 31=51 and 43=70

I have solved it -with or without maths running in my head -I do not know how or why but it just seem that my thought process sometimes skipped steps and methods and led me to the answer . Unscientific , irrational , or people just would called it a hunch but I do took my time thinking about the number as well and of course if there were such steps and methods that I unconsciously used -it is probably by elimination.

55-27=28, 28/2=14, 27+14 or 55-14 =41. My maths doesn't go beyond Scottish Higher grade B, have i fluked this?

Using elimination we can get: 2x =82 ; x=41 while y=14 x then is larger equal to 41.

Equation 1st is:- x+y=55 Equation 2nd is:- x-y=27 Taking 2nd equation: - x-y=27 x=27+y Then; Putting the value of x in equation 1st.... 27+y+y=55 27+2y=55 2y=55-27 2y=28 y=28/2 y=14 Again;Putting the value of y in equation 1st....... x+14=55 x=55-14 x=41 This is required Answers: -.........41

While the whole 2x = 82 =》x = 41 solution is more logical, I did something different to find both variables.

The addition and subtraction of y led me to understand that x is non negative so I found the difference between 55 and 27,

55 - 27 = 28

accounted for the number of times y was used in the equations (2) by dividing the difference by that number,

28/2 = 14

then substituted for y.

X + 14 = 55 =》x = 41, X - 14 = 27 =》x = 41

Simultaneous equations m8 bare easy, rearrange to make X the subject then substitute into the other one

Look bros I did it on the first try. In my head. It goes somethin like dis: x = 41 and y = 14. So, yall gots it now. Easy peasy lemon sqweezy. Make dat lemon aid brah!I hope I helped simplfy this issue for anyone who had trouble.BRAH!

AND

You can do this: (55+27)/2=41 for the greater one

Using elimination method:2y=28....y=14 ....substitute into one of the two equations to find the value for x....using second equation x-y=27;x-14=27...x=27+14=41..x=41;so x is d larger number so the answer is 41

Add the two equations, 2x=82 x=41 then 41+y=55 y=14 x is larger

x + y = 55 (1)

x - y =27 (2)

SUBTRACT (1) FROM (2)

2y = 28

y = 14

SUBSTITUTE y INTO (1)

x + 14 = 55

55 - 14 = 41 = x

I'm sure there was some formula or something for this, but I just used the fact that the numbers were related. I tried to simplify the problem by making the numbers smaller, so first I did: 3+2=5 and 3 - 2=1 where x=3 and y=2 So then I asked myself what is the relationship between the two answers, 5 and 1 I thought "well 5-1 is 4, and 4 divided by two gives me 2, the smaller number." Then I took this same question and scaled it up to the original. 55-27 is 28, and 28 divided by 2 is 14, which I assumed was the smaller number. Then I just subtracted 14 from 55 and got the larger number, which is 41

I'll probably have to go back and re-read the question, but if it was asking which variable was bigger, then that answer would have been x because if it was y, x-y would have been -27

BTW, I think I downvoted someone by accident while scrolling down on my phone, if it was you, just know it wasn't intentional :)

we have two statements
1) x+y = 55 2) x-y = 27

now take 2nd statement x-y=27 x=27+y

put the value of x in 1st statement (x+y=55)

27+y+y=55 27+2y=55 2y=55-27 2y=28 y=14

now for x value put value y in x=27+y x=27+14 x= 41

now we have x= 41 and y= 14 and x is greater

(55+27)/2 = 41

We need to solve both X and Y value to determine which has the larger value.

Since we have two unknowns we need two equation. (Eqn. 1 --> X + Y = 55) Eqn. 2 --> X - Y = 27

From Eqn. 1 X = 55 - Y ( Substitute this value to Eqn. 2)

Therefore, (55 - Y) - Y = 27 55 - 2Y = 27 55 - 27 = 2Y Y = 14

Thus the value of Y = 14. Substituting this value in equation X = 55 - Y,

X = 55 - 14 X = 41

Therefore the values are Y = 14 and X = 41

Clearly the X has the greater value which is equal to 41.

Simply sum bot the answers and divid with 2 you'll get the answer

Solve these equations by substitution method

x+y=55 x-y=27

55-27=28(=2y)

28/2=14(y)

X=55-14=27+14=41

X+Y =55, X=55-Y . 55-y- y=27 -2Y=-28. Y =14 (X-14)=27 X=41

x + y = 55

x - y = 27

55 - 27 = 2y, 2y = 28

y = 14 x = 55 - 14, x = 41

Greatest number between x & y when both the values are unknown can be found using the below formula:

Let the greatest number between x and y be g. Then, g=((x+y)+|x-y|)/2

(55-27)÷2=y=14 14+X=55 X=41

55-27=2*y=28 so y=14 and 27=x-14 so 27+14=x=41 result: 41 > 14

2x= 82 x= 41 y= 14

x+y=55 => x=55-y. Therefore x-y=27 can be written as, 55-2y=27. So y=14. Hense x=55-15. QED the value for x is the larger where x=41.

Named it first and second equation.. then take the value of x from equation 1..which is x=55-y

Now put it in 2nd equation instead of x..now solve it we get value of y which is 14 now put it in equation 1 and get the value of x..now tick the larger one..:)

55+27=82/2=41

x + y = 55 / x - y = 27 dividing the system 2x = 82 we obtain, as x = 41, y = 55- 41 making we obtain y = 14, so the greater is 41

55 and 27 are equidistant to x, therefore, x must be their average, hence, 41.

that was a comparison method...

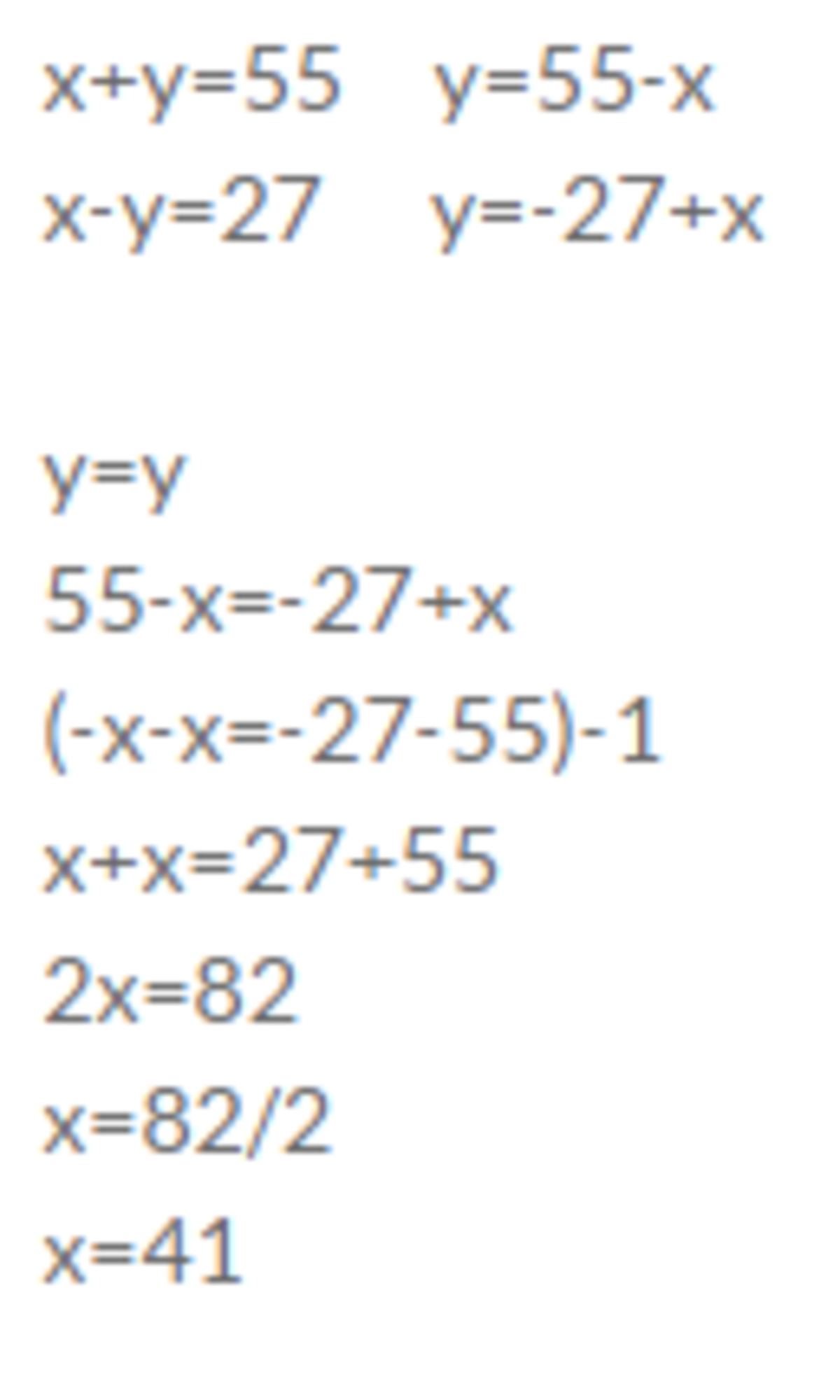and... this was a complete solution using comparison method :)

I think I put a little too much work into mine... Seeing that everyone else's solutions are extremely short. It didn't take me long at all to figure this out but my process I guess was longer than necessary. Anyways, here is my solution.

Equation 1: X + Y = 55 Equation 2: X - Y = 27 The first thing I did was determine which variable was larger and saw that X was larger due to the fact that if X has to be larger than Y in order for the solution to be a positive number in the second equation. So now we know what we are after, the value of X.

I started with Equation 2(Eq2) because that was were we got our information and it seemed the easier one to start with. I add Y to both sides to cancel Y out and also find a substitute value for X.

X - Y(+Y)= 27 + Y X = 27 + Y

I then plugged in the value of X into Eq1.

(27 + Y)+Y = 55

I simplified it.

27 + 2Y = 55

Then I begin to isolate Y by bringing the value 27 to the other side .

(27 - 27) + 2Y = (55 - 27)

Leaves us with...

2Y = 28

Then isolate Y by dividing by 2 on each side to cancel out the 2 attached to Y.

2Y / 2 = 28/ 2

Which gives us...

Y= 14

Now that we have found the value of Y we can find X, the solution and the larger number of the pair by plugging Y into one of the equations. In this example I use Eq1 to find the solution but you can use Eq2 as well.

X - 14 = 27

Isolate X.

X (- 14 + 14) = (27 + 14)

Therefore... X = 41.

Check your work by plugging the values into both problems and seeing that they both fit...

Equation 1: 41 + 14 = 55 Equation 2: 41 - 14 = 27

Now that you have both the variables,

X = 41 Y= 14

Submit the value of X as your solution because it is the larger of the pair as predicted in the beginning.

The end.

To not leave anything out....

The general strategy for these kinds of problem is,

1: Create one new equation using all the terms from both.

2: Eliminate the terms you don't want from the new equation.

3: Isolate the term whose value you want - so that it is all alone one side of the equation.

4: Calculate the value of the term whose value you want.

1: Create one new equation using all the terms from both.

There is no arithmetic that does this, you just need to understand how equality works. Let's use addition, but remember subtraction would work too...

(x+y) + (x-y) = 55+27

2: Eliminate the term you don't want - in this case it's y.

The left side of the new equation uses only addition and subtraction so we can loose the bracket and rearrange the terms...

x+x + y-y = 55+27

y-y = 0 which let's us drop the y entirely because x+x+0 is the same as x+x.

x+x = 55+27

3: Isolate the term you do want - so that it is all alone one side of the equation.

We want only one x in the whole equation and x + x is the same as 2x so let's do that...

2x = 55+27

And we want to get x on one side by itself. To get to just x on the left side we have to divide 2x by 2 which equals x. But that will ruin the equality so we have to divide the right side by 2 as well.

x/2 = (55+27) / 2

x = (55+27) / 2

4: Calculate its value.

x = 82 / 2

x = 41

All done.

I won't lie, but I guessed the answer.

Solution pretty simple 😊

X=55-Y...1 & -Y=27-X...2 Substitute equation 1 into equation 2 Therefore: -Y=27-(55-y) ➡ -Y-y=27-55+y ➡ -2y=28 ➡ y=14 Therefore: Substitute y into equation 1 X=55-14 ➡ x=41 Therefore: x is the largest variable at 41.

x + y = 55 x - y = 27

55 - 27 = 28 28 / 2 = 14 27 + 14 = 41

x = 41

if you know algebra you will find this easy as pie

x+y =55 ; x-y=27 ; y=55-x ; x -(55-x)=27 ; 2x=55+27 ; x=82/2 ; x=41

2x + y - y = 82 x= 41

55+27=82 82÷2=41 Easy solution

What can do is solve for one variable first (it doesn't matter which one you chose) x+y=55 => x=55-y x-y=27 Then replace the variable you solved for in the other equation with the amount it equals. x=55-y x-y=27 (55-y)-y=27 Then solve for y: (55-y)-y=27 55-2y=27 -2y=27-55 -2y=-28 2y=28 y=14 Then plug in y into the original equation: x+14=55 x=55-14 x=41

Try phrasing the question better, next time. I mean I get that the guy who made it is Indian and thus probably doesn't speak English as a first language (heck, this might have been originally written in Indonesian and just translated poorly), but come on, ". . . which of x,y is larger? Submit your answer as the larger number." is one of the most confusing things I've ever had to decipher. Try " . . . which of the two variables is larger? Submit the larger number as your answer." Put me in the problem-wording-creation field, coach. I'm ready.

Difference between 55 and 27 is 28, 28/2=14 27+14=41

x+y=55 - x-y= 27

2y = 28 (obviously it's y=14)

I picked x + y = 55 and substituted y=14 ---> x + 14 = 55 ---> x = 55 - 14 = 41

if y=55-x , we have x- (55-x)=27.==> 2x=27-28 ==> x=-28/2 Then, we have y=55-x=41

So simple! Just add the equations and you will get 2x=82 so x=41 and 41+y=55, y=14

x+y=55 x-y=27 after adding this two equations (x+y=55)+(x-y=27) 2x =82 then x=41 as x+y=55 then y=14 as we can see the larger one is x so thats our answer.... :)

Difference between 55 and 27 is 28, divided by two would give y (14) 27 + 14 = 41, or x

x+y=55 -> (1)

x-y=27 -> (2)

(1)-(2) =

2y=28

y=14

x=55-14=41

Solve for X first (subtract Y and add Y) X=55-Y and
X=27+Y

Therefore 55-Y=27+Y Solve for Y Y=14 (55=27+2Y) Return to X+Y=55
X= 41

we get the sum of the two equations x+y+x-y=55+27=82 , 2x=82 , x=41

I liked the way it was made confusing...that stmt made me read the question twice !!

Question is invalid. It says which of x,y is larger? Since x-y=27 and 27 is not negative x is always larger. No need to solve.

Tip... Subtitute a number given in the choices and look for a number that the sum is equal to 55 and the difference is equal to 27. And Tadaaaah ! XDD

X - Y = 27
X = Y+ 27 Y+27 +Y = 55 2Y+27 = 55 2Y = 28

Y = 14

X=55-14 X = 41

41+14 = 55 41-14 = 27

BIGGER NUMBER =(SUM+DIFFERENCE)/2 SMALLER NUMBER= (SUM-DIFFERENCE)/2

x+y=55 and x-y=27

If we solve both equations for x, we have:

x=55-y and x=27+y

Since x = both 55-y and 27+y, then we can conclude that 55-y=27+y Now we solve for y:

55-y=27+y (Subtract 27 from both sides.) 28-y=y (Add y to both sides) 28=2y (Divide 2 from both sides.) 14 = y

Now we know y=14, so we can solve for x:

x=55-y x=55-14 x=41

x is the larger number, and x=41, so the answer is 41.

x+y=55.
-× -x y=55-x

x-y=27

x-(55-x)=27

x+x-55=27

2×=27+55

2×=82

×=41 which is obviously greater than y

A.T.Q

2x = 82,

x = 41

y = 55-41

= 14

so the largest no. is x = 41.

Easy plug all the numbers into the equation for x because x is obviously the larger quantity solve for y if y is the same in both equations you get your answer lol

You can solve it by simultaneous method

Or, look at the possible answers subtract the amount for y you could have to make the answer true, now apply it to the first problem, does it match? The only one that satisfies both is 41, because 41-14=27 and 41+14=55 Therefore it is 41.

+y and -y get cancel Then 2x=82 X=41

41–55=14 and 41–14=27

Although I went a roundabout way of doing it. I got 41.

2X = 82

x = 41

41+y =55

y = 55-41

y =14

X is greater than y

Look for the value of x using the second equation: [1] x - y = 27 [2] x = 27 +y Substitute the value of x to the first equation: [3] x + y = 55 [4] (27 + y) + y = 55 Find the value of y: [5] 27 +y+y=55 [6] 27+2y=55 [7] 2y = 55 - 27 [8] 2y = 28 [9] 2y/2 = 28/2 y=14 Find the value of x: [10] x + y = 55 [11] x + 14 = 55 [12] x = 55 - 14 x = 41

X+y=55. & x-y=27.
So add given equation 2x=82. X=41 41+y=55.
So. Y=14 So greatest is x=41

x+y=55...1 x-y=27....2 1+2 2x=82 x=82/2=41 answer

Start from 55 and work your way down. Once you reach 41, you will find that 41+14=55 and 41-14=27

took me 15 seeconds

Just add both sets of eq.

X+y=55 X-y=27 +y and -y cancel we get 2x=82 X=82/2=41

The difference between the two values is 28. x is constant in both formulae. The difference betwene the two values is also 2y, therefore 28/2 = 14. 55-14 = 41, 27 + 14 = 41 therefore x =41

how much a month?

X+Y=55 (1)

X-Y=27 (2)

Obviously X is the larger number.

In (2) X is bigger than Y by 27 : X=27+Y

Then (1) looks like this (27+Y)+Y=55

And since 55-27=28, that's the sum of the 2 Ys

28÷2=14 that's the value of Y

Therefore X=55-14 which equals 41.

To answer the question of the larger the second equations tells that $x$ is larger....

so we have to find $x$

From the equations using Linear Elimination Method

$x+y=55 ....(1)$

$x-y=27 ....(2)$

From which we get $.....2x =82$

$\therefore \boxed{x=41}$

X+y= 55 X-y= 27,

x=55-Y x=27+y

55-Y=27+y

2y=28

Y=14, x=41

(55 - 27) ÷ 2 = y

55 - y = x

or

27 + y = x

X+Y=55 X-Y=27

-y+y cancels out x+x=2x 55+27=82 2x=82 2x/2 ...82/2 X=41

the easiest one in this case: x + y = 55 (1) x - y = 27 (2) 2x = 82 => x = 82/2 = 41 (here you can verify y to see which is greater but it's pretty clear )

1+1=2 i think

Omg people put so much thought into this, it's simple substitution..... (x+y=55) solve for x... (x=55-y)... Substitute this new equation for x in the second equation... (x-y=27) becomes... (55-y-y=27) solve for y... (55-2y=27)... (-2y=-28)... (2y=28)... (y=14)... (55-14=41)

By hit and trial... Let X=40,Y=15 ,X+Y=55 ✅ X-Y=25 ❎ Let X=41,Y=14 ,X+Y=55 ✅ X-Y=27 ✅ That's how I solved it !

Substituting 55 for x+y, and 27 for x-y, then by the transitive property (x+y)+(x-y) must equal 82: (55+27). Such as (x+y)-(x-y) equals 27. From here you can reduce the first equation to as follows: (x+y)+(x-y) = 82 (x+y)+(x) = 82-y X+x = 82 2x/2 =82/2 X = 41 55-41 = 14 = y To check your work you can take the second equation to solve for y.