Randomly plotting the angle
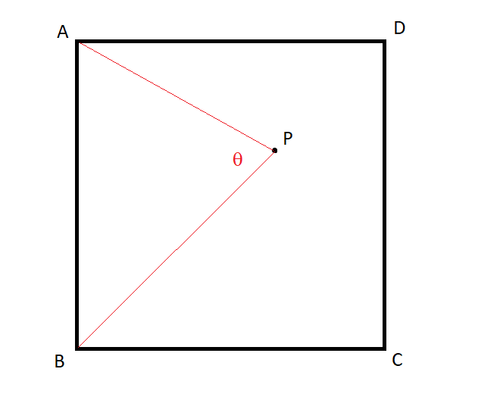
A B C D is a square; and P is a random point inside it. Find the expected angle of θ in degrees.
Bonus: Find the probability density function of θ .
Find the median angle instead .
Fidn the mode angle instead .
The answer is 90.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
OMG, this is simpler than I thought.
Log in to reply
Same here - I coded it first, got 8 9 . 9 ∘ , then realised why! The proof felt like such a cheat after getting my laptop to do the hard work.
This seems to get tricky if A B C D is a rectangle...
Log in to reply
Lemme work on a rectangular version and see what I can come up with.
Log in to reply
I've managed to get a closed formula that matches computed values, but it's not pretty. I can share it here, or shall I post it as a solution to your next problem? ;-)
Log in to reply
@Chris Lewis – Go ahead and post it as your own problem then. Here is the raw text:
1 2 3 4 5 6 7 |
|
Log in to reply
@Pi Han Goh – Thanks - will do, I'm just looking for a rectangle where the exact answer isn't too horrific (spoiler alert: it's usually horrific)
Log in to reply
@Chris Lewis – Yeah, I'm working on it as we speak. I'm also simultaneously working on the solution that James Arruda claimed , that the optimal expected value is 3.60 something something something....
Log in to reply
@Pi Han Goh – OK...posted...but it's not pretty! The approach you were looking at in your solution here (using cosine rule) is different to mine, so maybe (hopefully) there's a neat way to solve for rectangles too. Please upload a solution if you find one!
Log in to reply
@Chris Lewis – I randomly guessed some integers and got it right. I still can't solve it though and I'm weeping right now.
Log in to reply
@Pi Han Goh – Uh-oh...sorry, not the intention!!! Still, glad you got it right. I'm betting I've missed something way easier than my approach there.
@Chris Lewis – It definitely depends on the dimensions. And I guess that the ratio will definitely be involved there as well
Log in to reply
@Mahdi Raza – it actually depends on 1 dimension only. Without the loss of generality, we can assume the dimensions of the rectangle to be 1 × M .
Log in to reply
@Pi Han Goh – Ok, so you are saying that if we consider dimensions to be ( a , b ) it is equivalent to say that the dimensions are ( 1 , a b ) where a b = M . Makes sense. Because angles do not depend on the size.
Log in to reply
@Mahdi Raza – Yuppers.
By the way, super big fan of your animations in the Daily Challenges!
Log in to reply
@Pi Han Goh – Great! What should be the next step... any hints if you've figured it out?
Thank you so much though!! 😊 😊
Log in to reply
@Mahdi Raza – Haha, I'm as lost as you are. I'm just fumbling around by doodling random alien symbols, praying to God for a sign.
Log in to reply
@Pi Han Goh – lol, I should start praying too then ;)
Oh Wow wow! really simple once you know it...
That is my first thought of trying to solve the "Inspiration" question, but then figure it out the 4 angles will have some instance to be acute at the same time. That is the right time to use this argument!
Instead of finding the mean of this angle, what about its median? Monte-Carlo suggests it's around
1.384
.
Log in to reply
Could be a coincidence, but that's very close to 8 0 ∘ . You mention finding the probability distribution in the question - did you manage to get an expression for that?
Log in to reply
Well, the other solution poster pointed out that:
θ = π − 2 tan − 1 ( x y ) , where x , y are independent and identical continuous uniform distribution, U ∼ [ 0 , 1 ] . That's all I can gather.
Sure enough, five weeks later...
If the coordinates of P are ( x , y ) , then θ = tan − 1 x y + tan − 1 x 1 − y
Taking the tangent of both sides, tan θ tan θ ( x 2 − y + y 2 ) tan θ = 1 − x y ⋅ x 1 − y x y + x 1 − y = x 2 − y + y 2 x = x
which we recognise as the equation of a circle. In fact, it's the equation of a circle with centre ( 2 1 cot θ , 2 1 ) and radius 2 1 csc θ . As you might intuitively expect, this circle passes through ( 0 , 0 ) and ( 0 , 1 ) as well.
If we fix θ , the intersection of this circle with the original square is the locus of points P such that ∠ A P B = θ .
To find the median value of θ , then, we just need to find the value of θ so this locus splits the square into two regions of equal area.
The region enclosed by the locus and the square is made up of a rectangular portion and a circular segment. Its area is given by cot θ + 8 sin 2 θ 2 θ − sin 2 θ
We want this equal to 2 1 . Solving numerically, we find θ = 1 . 3 8 4 1 … for the median.
Log in to reply
Once you're done, post it as a problem of your own, and let me cry because I can't solve it.
Also, don't forget to work on the mode as well, which is about 1 . 2 5 3 1 3 1 rad ≈ 7 1 . 8 ∘ .
Log in to reply
Well, I daren't post it, as we seem to have a discrepancy - any ideas?? I'll have a look at the mode, but meantime I found it useful to look at this on Desmos - that's when I realised it was just a bit of a circle all along. If you paste this...
\arctan\left(\frac{y}{x}\right)+\arctan\left(\frac{1-y}{x}\right)=c\left{0<y<1\right}\left{0<x<1\right}
...into Desmos you should get a slider that lets you play with the graph.
Log in to reply
@Chris Lewis – Well, I'm pretty sure my results are correct (to the first few decimal places). I've posted my Monte Carlo simulation under Arghyadeep's solution.
Log in to reply
@Pi Han Goh – Yep, you were right! (This, by the way, is why I almost always Monte Carlo these things first; I - correctly - have zero faith in my ability to crunch through these equations mistake-free!!)
Log in to reply
@Chris Lewis – By the way, how did you work out the mode?
Log in to reply
@Chris Lewis – No idea. I'm still thinking about it. Maybe differentiate the integrand and find the maximum point??
Log in to reply
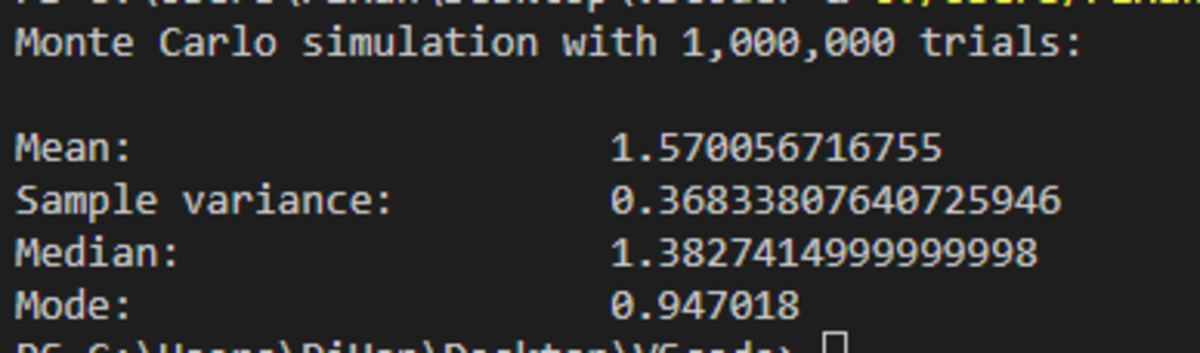
@Pi Han Goh – You mentioned you had found it was 1 . 2 5 3 … using Monte Carlo, but I seem to be finding it's a bit less than one. (I've tried both MC and just scanning the space with a fine grid; I counted the number of times the angle was in each interval ( 0 . 7 5 , 0 . 8 ) , ( 0 . 8 , 0 . 8 5 ) etc; the modal interval seems to be coming out as somewhere around 0 . 9 5 for me).
Log in to reply
@Chris Lewis – You're right. Sorry my bad. I've reduced the amount of trials to test something and the value fluctuates badly.
Log in to reply
@Pi Han Goh – Ah, OK, thanks. Well, I've found a value around that one via a couple of different numerical methods; my analytical approach is not working at all yet.
Summoning @Mark Hennings because he seems to be unbelievably great at this area.
To Mark:
In this problem, we have found the expected value of ∠ A P B to be exactly 9 0 ∘ . Arghyadeep's solution shows a clean calculus solution. I tried working on a closed-form for the variance of this same angle, and it all boils down to 0 ∫ 1 0 ∫ 1 ( tan − 1 ( x y ) ) 2 d y d x , which even Mathematica can't seem to tackle.
Next, I thought about finding the median and mode. And I've worked them out with a Monte-Carlo simulation (under Arghyadeep's solution), but nothing seems to come to fruition.
Log in to reply
Using the double variable substitution u = x y , v = y / x , we have the Jacobian ∂ ( x , y ) ∂ ( u , v ) = x 2 y = 2 v and hence the integral J = ∫ 0 1 ∫ 0 1 ( tan − 1 x y ) 2 d x d y = 2 1 ∫ 0 ∞ d v ∫ 0 m i n ( v , v − 1 ) d u v − 1 ( tan − 1 v ) 2 = 2 1 ∫ 0 1 ( tan − 1 v ) 2 d v + 2 1 ∫ 1 ∞ v − 2 ( tan − 1 v ) 2 d v = 2 1 ∫ 0 1 ( ( tan − 1 v ) 2 + ( 2 1 π − tan − 1 v ) 2 ) d v = ∫ 0 1 ( tan − 1 v ) 2 d v − 2 1 π ∫ 0 1 tan − 1 v d v + 8 1 π 2 Integrating by parts, ∫ 0 1 tan − 1 v d v = [ v tan − 1 v ] 0 1 − ∫ 0 1 1 + v 2 v d v = 4 1 π − [ 2 1 ln ( 1 + v 2 ) ] 0 1 = 4 1 π − 2 1 ln 2 so that J = ∫ 0 1 ( tan − 1 v ) 2 d v + 4 1 π ln 2 Integrating by parts twice more: J = [ v ( tan − 1 v ) 2 ] 0 1 − ∫ 0 1 1 + v 2 2 v tan − 1 v d v + 4 1 π ln 2 = 1 6 1 π 2 + 4 1 π ln 2 − [ tan − 1 v ln ( 1 + v 2 ) ] 0 1 + ∫ 0 1 1 + v 2 ln ( 1 + v 2 ) d v = 1 6 1 π 2 + ∫ 0 4 1 π ln ( sec 2 θ ) d θ = 1 6 1 π 2 − 2 ∫ 0 4 1 π ln ( cos θ ) d θ = 1 6 1 π 2 + 2 1 π ln 2 − G where G is the Catalan constant.
Similarly, but more simply, we have K = ∫ 0 1 ∫ 0 1 tan − 1 x y d x d y = 2 1 ∫ 0 ∞ d v ∫ 0 m i n ( v , v − 1 ) d u v − 1 tan − 1 v = 2 1 ∫ 0 1 tan − 1 v d v + 2 1 ∫ 1 ∞ v − 2 tan − 1 v d v = 2 1 ∫ 0 1 ( tan − 1 v + 2 1 π − tan − 1 v ) d v = 4 1 π
BTW Wolfram Alpha may not be able to handle evaluating J , but Mathematica makes short work of it.
Log in to reply
@Mark Hennings – Be right back. I have to refill my printer, in the middle of this pandemic.
@Mark Hennings – I want to say that I totally forgot about using Jacobian, but I'm pretty I can't finish it as you have done it.
You have my utmost gratitude again.
Would you like to post this variance question? Or would you like me to do it?
Log in to reply
@Pi Han Goh – We're also going to have to work out the double integral of tan − 1 ( x y ) tan − 1 ( x 1 − y ) . I haven't done that one yet...
@Mark Hennings – Simply wow!!!! @Mark Hennings . A variable change did not cross my mind even for once.
this value seems to be π minus the value you found - any idea which one of us went wrong where?
Yeah, I'm still reading through this. I can't spot any error.... yet.
Log in to reply
Wait... to be honest, I still don't understand your solution.
Log in to reply
@Pi Han Goh – Never mind, I found my mistake - I had
θ = tan − 1 y x + tan − 1 1 − y x
when I should have had θ = tan − 1 x y + tan − 1 x 1 − y
It's close, though! Editing now...
Log in to reply
@Chris Lewis – Right, I've edited my comment and we do get the same answer.
Sorry I wasn't clear. What I was trying to do was think about the probability a bit geometrically. The locus of points giving the same θ value divides the square into two regions; one (green) where the angle A P B is bigger than θ , and one where it's smaller (blue). The probability of being in one of these regions is equal to the area of that region (since the probability space has unit area).

At the median θ value, these two regions will each have area 2 1 (by definition of the median). So if we can find the area, we get an equation for θ . The good news is, the locus is part of a circle; the bad news is, it's a segment, so the solution has to be numerical.
I hope that makes sense!
Delightful. Do you want me to post the median question? Or would you like to do it yourself? (I still can't understand your solution... yet)
@Chris Lewis , see this link . Feel free to paste this as your own problem statement for the median.
Log in to reply
Thanks - although you came up with this problem (and wrote it up, too)! I'd say either post it yourself or perhaps this could be part of a discussion? (You've had some cool ideas to explore here, but I'm worried they'll get a bit lost in these comments/replies).
@Arghyadeep Chatterjee + Chris Lewis + Mark Hennings
check this out The median version
Hahahha, I've made a booboo. It turns out that if we want to know the variance, we ALSO need to know the value of 0 ∫ 1 0 ∫ 1 tan − 1 ( x y ) tan − 1 ( 1 − x y ) d y d x , which is approximately 0 . 6 2 8 2 2 1 8 > 5 π .
Let me see if I can work this out by myself first.
Log in to reply
To clarify, the angle ∠ A P B : = θ = π − tan − 1 ( x y ) − tan − 1 ( 1 − x y ) . We have already discovered its expected value to be π / 2 .
To find its variance, we are left to find its second moment. That is, 0 ∫ 1 0 ∫ 1 θ 2 d y d x . Expanding this gives
π + 2 ∫ 0 1 ∫ 0 1 [ tan − 1 ( x y ) ] 2 d y d x − 4 π ∫ 0 1 ∫ 0 1 [ tan − 1 ( x y ) ] d y d x + 2 ∫ 0 1 ∫ 0 1 [ tan − 1 ( x y ) tan − 1 ( 1 − x y ) ] d y d x
The first two iterated integrals has already been computed to be 1 6 π 2 + 2 ln 2 π − G and 4 π , respectively. What's left is the last integral, which Mathematica failed to tackle.

Log in to reply
@Pi Han Goh . I think I made a bad decision to write the angle expression as π − a r c t a n ( x y ) − a r c t a n ( 1 − x y ) . Simply writing it as a r c c o t ( y x ) + a r c c o t ( y 1 − x ) makes more sense.
I created the below gif using GIFsmos to show the locus I was referring to above a bit more clearly. The red line on each frame corresponds to all the points P in the square such that ∠ A P B = θ , as θ varies from 4 1 π to π :
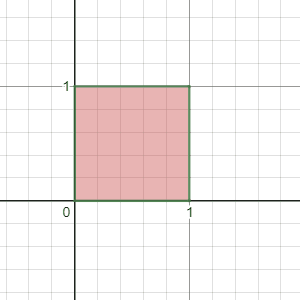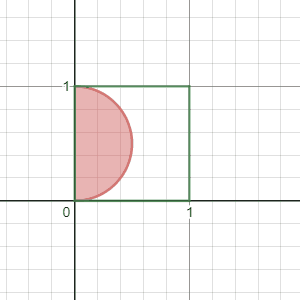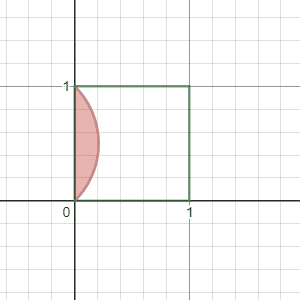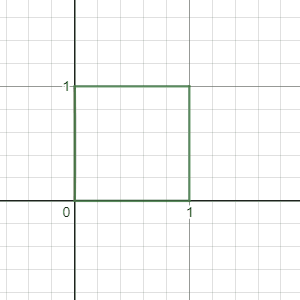
The red region is the set of points such that ∠ A P B > θ . Since we're equally likely to choose any point in the square, the area of the red region gives Pr ( ∠ A P B > θ ) . The complement of this is therefore the cumulative distribution function!
As above, it turns out the red line is part of a circle (centre ( 2 1 cot θ , 2 1 ) and radius 2 1 csc θ ). The qualitative shape of the red region depends on θ , as you can see in the animation; but it's not too hard to work out that ( Pr ( ∠ A P B ≤ θ ) = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ 1 − [ 4 3 cot θ + 4 sin 2 θ θ − tan − 1 2 − cot θ 4 cot θ − 3 − ( cot θ − 2 ) 4 cot θ − 3 ] if 4 π ≤ θ < 2 tan − 1 2 1 1 − cot θ − 8 sin 2 θ 2 π − 2 θ + sin 2 θ if 2 tan − 1 2 1 ≤ θ < 2 π 1 − 8 sin 2 θ 2 π − 2 θ + sin 2 θ if 2 π ≤ θ < π
(If I can simplify this further I will!)
The cumulative distribution and probability density (found by differentiating the cdf) look like this:
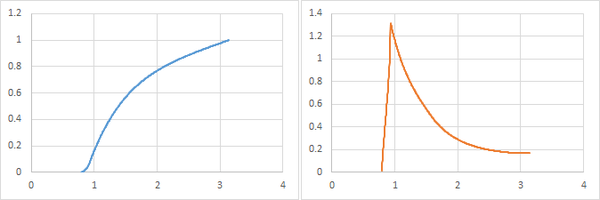
The cdf lets us solve for the median; as above, we get θ = 1 . 3 8 … .
The pdf lets us solve for the mode; it seems (proof to come, I hope) that this occurs at θ = 2 tan − 1 2 1 (this is the value where the circle is tangent to the side of the square x = 1 ).
If anyone could help get these expressions a bit neater I'd appreciate it! Wolfram|Alpha did some simplification, but didn't manage to compute the second derivative of the cdf everywhere.
Log in to reply
This is amazing work. I'm still digesting this since yesterday. And I'm still struggling with your solution for my median question.
Will update that you once I got something useful.
Log in to reply
Thanks! I wonder if it might be useful for the variance question too (though I suspect not - I think the way you're going with integrating over the square is more likely to work). If you've any specific questions let me know and I'll try to make it clearer.
I doubt it will get much less complicated. I have, in principle, an explicit expression for the variance of θ , but it is horrendous! I need, amongst other things, the integral ∫ 0 1 tan − 1 x tan − 1 ( 1 − x ) d x which evaluates in terms of arctrig functions, logarithms and polylogarithms. I have not (yet) managed to simplify this down to something that can be lived with
@Mark Hennings @Chris Lewis @Arghyadeep Chatterjee
I've posted a MODE version as well
Feel free to post all your findings there.
Let us consider AB to be the x-axis . Now let the point be ( x , y ) where x and y are uniformly and independently distributed on ( 0 , 1 ) . Hence our Probability Density Function is just:- f ( x , y ) = 1 when 0 < x < 1 , 0 < y < 1 and 0 elsewhere .
Now the ∠ A P B = π − tan − 1 ( x y ) − tan − 1 ( 1 − x y ) in radians.
Hence the expected value is :-
∫ 0 1 ∫ 0 1 ( π − tan − 1 ( x y ) − tan − 1 ( 1 − x y ) ) d y d x .
Now the definite integral of tan − 1 ( x y ) and tan − 1 ( 1 − x y ) over 0 < x < 1 will have same value due to symmetry......one can even substitute z = 1 − x to show that the second integral is indeed the same as the first integral.
So we have :-
∫ 0 1 ∫ 0 1 ( π − 2 ⋅ tan − 1 ( x y ) ) d y d x .
Now we can substitute y = t x such that d y = x d t so that our integral becomes easier to compute.
We have ∫ 0 1 ∫ 0 1 tan − 1 ( x y ) d y d x = ∫ 0 1 ∫ 0 x 1 x tan − 1 ( t ) d t d x .
We know ∫ tan − 1 ( x ) d x = x tan − 1 ( x ) − 2 1 ln ( 1 + x 2 ) + C .
So we have ∫ 0 1 ( tan − 1 ( x 1 ) − 2 x ln ( 1 + x 2 1 ) ) d x = ∫ 0 1 ( 2 π − cot − 1 ( x ) − 2 x ln ( 1 + x 2 1 ) ) d x
Now we know ∫ cot − 1 ( x ) d x = x cot − 1 ( x ) + 2 1 ln ( 1 + x 2 ) + C .
Also the integral involving the natural logarithm ( ln ) can be evaluated using substitution x 2 = u so it becomes of the form ∫ ln ( u + 1 ) − ln ( u ) d u
Hence using these results we arrive at the conclusion that ∫ 0 1 ∫ 0 1 tan − 1 ( x y ) d y d x = 4 π
Hence our expected value is π − 2 ⋅ 4 π = 2 π = 9 0 °
Perfect. I was looking for a calculus solution and I gave up after 1 week. But you pulled it off! DELIGHTFUL!!!!!!
Let me work on the variance of the angle formed (angle APB), because I'm a sadist.
Log in to reply
OMG....variance!!!! Now that would be a challenge. I cannot even begin to think how am I going to solve the square of that integrand...lol
Log in to reply
If it helps, I've done a Monte-Carlo simulation in Python and I get a (sample) variance of about 0.368
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
|
Log in to reply
Log in to reply
@Pi Han Goh – It appears that Mathematica can't evaluate this integral at all. So I'm pretty pessimistic to find a closed-form for V a r [ ∠ A P B ] .

Log in to reply
@Pi Han Goh – It all boils down to computing 0 ∫ 1 0 ∫ 1 ( arctan ( x y ) ) 2 d y d x
Log in to reply
@Pi Han Goh – @Pi Han Goh yeah exactly....it is hopeless to try and find the closed form of the variance. Either monte carlo or numerically approximating the integral is the only hope sadly.
Log in to reply
@Arghyadeep Chatterjee – What about the mode and the median? heheheheheehehe
Log in to reply
@Pi Han Goh
–
My MC above shows that the median is about
1.384
.
Log in to reply
@Pi Han Goh – Mode should not be very hard to find. It is a maxima problem for two variables but median will be tough to do by hand.
Log in to reply
@Arghyadeep Chatterjee
–
My MC above shows MODE approx
1.253
.
I'm still working on this.
Log in to reply
@Pi Han Goh – @Arghyadeep Chatterjee , see Mark Hennings' comment under Chris Lewis' solution.
Disclaimer: This is incomplete.
Let A ( 1 , 0 ) , B ( 0 , 0 ) , P ( r 1 , r 2 ) , where r 1 , r 2 are two identical identical random variable that follows the uniform distribution U ∼ ( 0 , 1 ) .
Using cosine rule , we have ∠ A P B = cos − 1 ( A P ⋅ B P ( A P ) 2 + ( B P ) 2 − ( A C ) 2 ) .
With A B = 1 , and A P , B P can both be measured using the distance formula .
Then, ∠ A P B is
-
larger than 9 0 ∘ if ( A P ) 2 + ( B P ) 2 − 1 < 0
-
smaller than 9 0 ∘ if ( A P ) 2 + ( B P ) 2 − 1 > 0
Substitute and simplify, we have 2 ( A P ) 2 + ( B P ) 2 − 1 = r 1 2 + r 2 2 − r 1 r 2 = r 1 − r 2 r 1 3 − r 2 3 (as the probability of r 1 − r 2 = 0 is 0).
In other words,
-
∠ A P B > 9 0 ∘ if r 1 < r 2 .
-
∠ A P B < 9 0 ∘ if r 1 > r 2 .
Since P r [ r 1 > r 2 ] = P r [ r 1 < r 2 ] = 2 1 , it is equally likely that the angle ∠ A P B is larger or smaller than 9 0 ∘ . Hence, the expected value in question is 9 0 ∘ .
You might notice that my solution is flawed because I didn't justify that the probability density function of θ is symmetric at θ = 9 0 ∘ .
Yes, cosine rule!! Nice thinking, should have thought of that as standard approach for two different lengths in rectangle as well...
How about put the figure into the co-ordinate plan? Setup the equation of the two lines pass thru A ( 0 , 0 ) , B ( 0 , 1 )
Then the product of the slopes m × n = x 2 y ( y − 1 )
As x , y ~ U ( 0 , 1 ) and x , y are iid (independent and identically), E ( m × n ) = − 1 ⟹ the expected angle = 9 0 °
For rectangle cases, we may use same method to find out the value. Just aware the size length is smaller length or longer length (x,y) of rectangle.
Log in to reply
NiCEEEEEEEEEEEE. How do we do evaluate that integral by hand?

The expected values of ∠ A P B , ∠ B P C , ∠ C P D and ∠ D P A will (by symmetry) all be the same; call this value θ .
So the expected value of ∠ A P B + ∠ B P C + ∠ C P D + ∠ D P A will be 4 θ .
But, for any point P in the interior of the square, ∠ A P B + ∠ B P C + ∠ C P D + ∠ D P A = 3 6 0 ∘ .
Hence θ = 9 0 ∘ .