Rational Approximation of numbers

With enough patience, we can get the continued fraction of $\sqrt[3]{10}$ to be $[2;6,2,9,1,1,2,4, \ldots ]$

So we want to input as much nested fractions, trial and error shows that for constraint for numerator and denominator to be less than $1000$ would give the fraction below (with natural number $x$ )

$\LARGE 2 + \frac {1}{ 6 + \frac {1}{2 + \frac {1}{9 + \frac {1}{1 + \frac {1}{1+x}}}} } = \frac {293x+558}{136x+259}$

Substitute $x = 1$ gives $a = 851, b = 395$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

S=10**(1.0/3)
def closeness(a,b):
    P=a/b
    if (S>P):
        return S-P
    else:
        return P-S
lista=[]
for b in range(1,500):
    for a in range(2*b,1000):
        lista.append((closeness(a,b),a,b))
lista.sort()
lista[0]

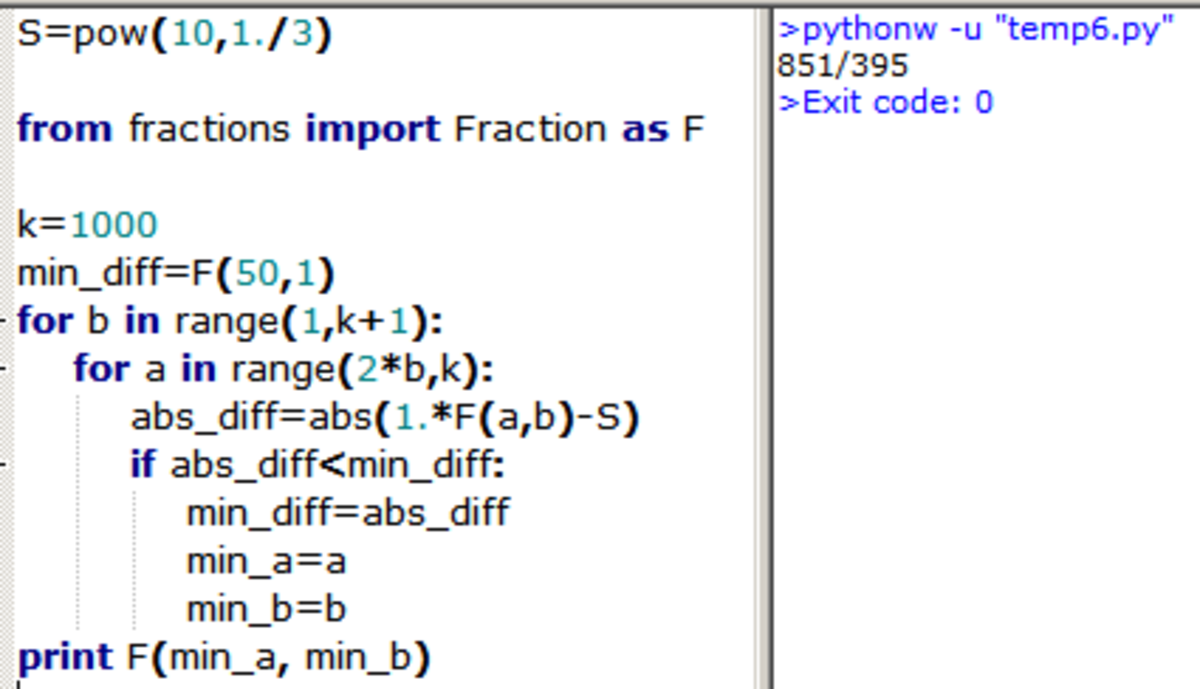
It returns (4.310285048436668e-06, 851, 395)

Here is a beginner's way to solve this problem: brute force. The code below is self explanatory:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

#include<iostream.h>
#include<conio.h>
#include<math.h>

//brute irrational root approximator.

int main()
    {
    clrscr();
    double n,a,p;
    cout<<"enter a in a^(n)"<<endl;cin>>a;
    cout<<"enter (1/n) in a^(n)"<<endl;cin>>p;
    n=1/p;n=pow(a,n);
    cout<<"enter upper bound for numerator and denominator"<<endl;
    cin>>a;
    double d=100,num,den;
    for(double i=1;i<=a;i++)
        {
        for(double j=1;j<=a;j++)
            {
            double k=(i/j);
            k=k-n;
            (k>0)?k=k:k=-1*k;
            if(k<d)
                {
                d=k;
                num=i;den=j;
                }
            }
        }
    d=num/den;
    cout<<n<<endl<<d<<" = "<<num<<"/"<<den;
    getch();
    return 0;
    }

python 2.7: gives 1246

def f(x,d,k):

for a in range(1,k):

    for b in range(1,k):

        P = a/b

        e = abs(P-x)

        if e < d:

            print(e,a,b)

x is the value we wish to find a close fraction for. d is our delta value, i.e. our acceptable margin of error. k is how large our domain of natural numbers should be.

I used Python or this code. Essentially I wrote a double for loop to let Python go through every value of a/b, but ignore those that had a margin of error larger than my delta requirement. I then looked at the printed values and chose the a and b that resulted in the smallest epsilon, or error, value. The "a" and "b" that led to this were 851 and 395.

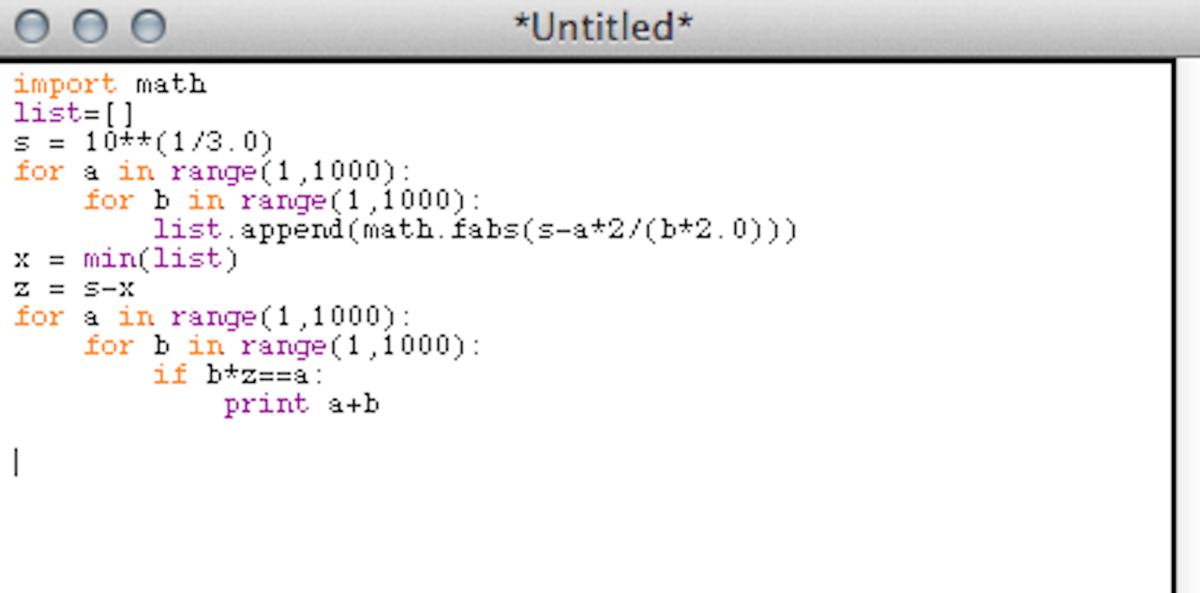
One need not search the entire space of (a,b)'s. Indeed, the following code could be tightened. The variable 'k' is present because I was checking the code for smaller values of it.