Real roots again?
Consider the polynomial P n ( x ) = x n + x n − 1 + x n − 2 + … + x + 1
Find the maximum no.of distinct real roots it can have if n is a positive integer strictly less than 1000.
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Hi, would you please explain to me how did you decide to define G n ( x ) the way you did ?
Log in to reply
I guess because the roots of r = 0 ∑ n − 1 x r are all the n th roots of unity except 1 .
Or, you could simply apply the "formula" for the sum of the terms of a geometric sequence and see that x − 1 appears in the denominator. Multiply to get rid of it.
Log in to reply
Thanks bro, nice observation . Considering that you are just two years my junior, your mind is quite sharp :)
Log in to reply
@Honey Singh – Lol I'm actually 17 :P
@Honey Singh – Are you the singer Honey Singh ? I'm asking this since your age is also 31
Log in to reply
@A Former Brilliant Member – I wish I weere , but no i am his fan . of 31 years too
from where did u get this property mentioned ion 1st line?
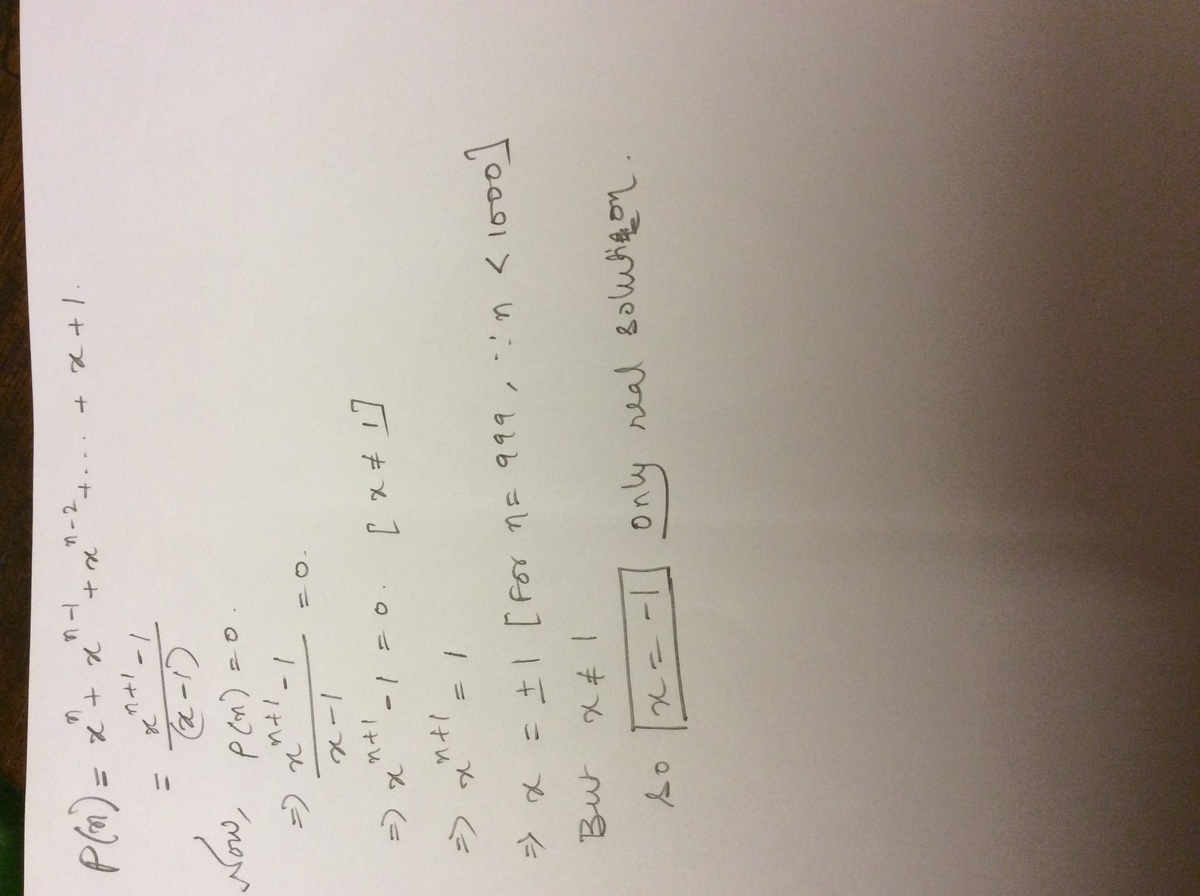
Define another polynomial G n ( x ) = ( x − 1 ) P n ( x )
So, G n ( x ) = x n + 1 − 1
If G n ( x ) = 0 , then x n + 1 = 1
If n + 1 is even, then we get two distinct real solutions, − 1 and 1 .
If n + 1 is odd, then we get only one real solution, 1 .
In each case one solution comes from the factor ( x − 1 ) .
So, P n ( x ) can have only 1 real solution.