Reciprocal Sums

Calculus Level 1

It is known that 1 1 + 1 2 + 1 3 + ⋯ \frac{ 1}{1} + \frac{1}{2} + \frac{1}{3} + \cdots is infinite.

What about

1 1 2 + 1 2 2 + 1 3 2 + ⋯ ? \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \cdots \ ?

Hint:

It is finite and less than 2 It is finite and equals 2 It is finite and greater than 2 It is infinite

Calvin Lin by Calvin Lin

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Chew-Seong Cheong
Jun 10, 2017

As shown in the diagram:

S = 1 1 2 + 1 2 2 + 1 3 2 + 1 4 2 + 1 5 2 + 1 6 2 + 1 7 2 + 1 8 2 + . . . < 1 1 2 + 1 2 2 + 1 2 2 + 1 4 2 + 1 4 2 + 1 4 2 + 1 4 2 + 1 8 2 + . . . < 1 1 + 1 2 + 1 4 + 1 8 + . . . = 1 1 − 1 2 = 2 \small \begin{aligned} S &= \frac 1{1^2} + \frac 1{2^2} +{\color{#3D99F6}\frac 1{3^2}} + \frac 1{4^2} + {\color{#3D99F6}\frac 1{5^2} + \frac 1{6^2} + \frac 1{7^2}} + \frac 1{8^2} +... \\ & < \frac 1{1^2} + \frac 1{2^2} +{\color{#D61F06}\frac 1{2^2}} + \frac 1{4^2} + {\color{#D61F06}\frac 1{4^2} + \frac 1{4^2} + \frac 1{4^2}} + \frac 1{8^2} +... \\ & < \frac 1{1} + \frac 1{2} + \frac 1{4} + \frac 1{8} +... = \frac 1{1-\frac 12} = 2 \end{aligned}

Therefore, it is finite and less than 2 .

5 Helpful 0 Interesting 0 Brilliant 0 Confused
Aviel Livay
Feb 11, 2017

It's f i n i t e \boxed{finite} and also < 2 \boxed{<2}

Why?

Let's denote S = 1 1 2 + 1 2 2 + 1 3 2 + . . . . . S=\frac{1}{1^2}\ + \frac{1}{2^2}\ + \frac{1}{3^2}\ + .....

Now let's write down some comparisons:

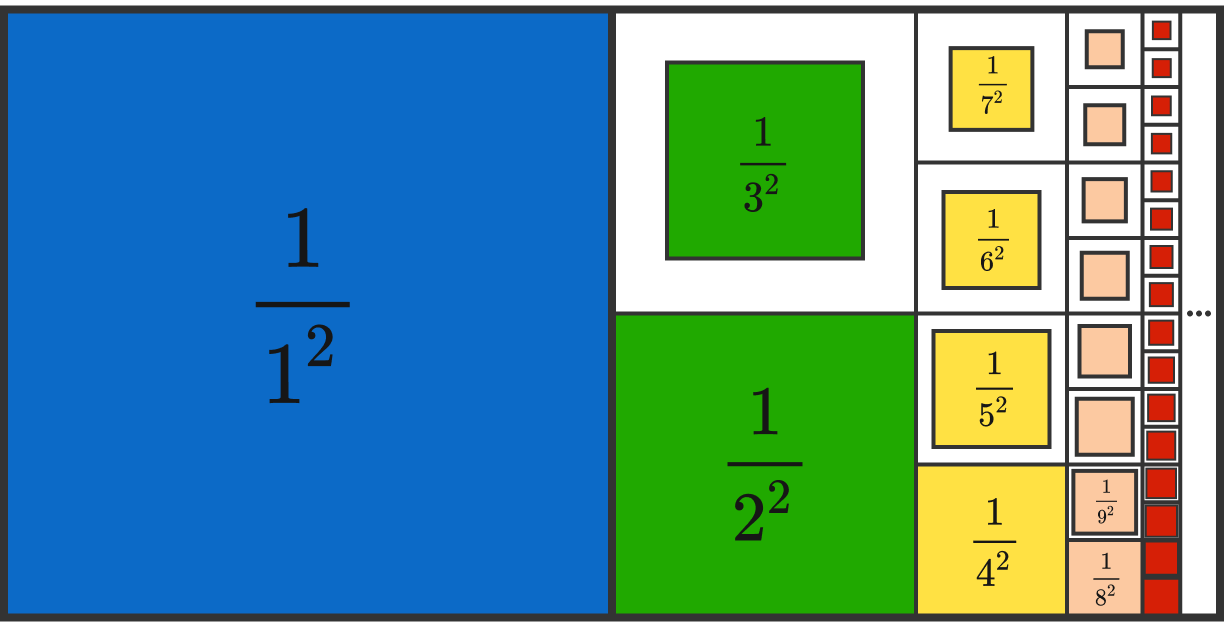
On the LHS we shall write elements of S S and on the RHS we shall put elements of the image presented.

Blue: 1 1 2 = 1 \frac{1}{1^2} = 1

Greens: 1 2 2 + 1 3 2 < 1 2 \frac{1}{2^2} + \frac{1}{3^2} < \frac{1}{2}

Yellows: 1 4 2 + 1 5 2 + 1 6 2 + 1 7 2 < 1 4 \frac{1}{4^2} + \frac{1}{5^2} + \frac{1}{6^2} + \frac{1}{7^2} < \frac{1}{4}

And the general case: 1 ( 2 N ) 2 + 1 ( 2 N + 1 ) 2 + 1 ( 2 N + 2 ) 2 + . . . 1 ( 2 N + 1 − 1 ) 2 < 1 2 N \frac{1}{{(2^N)}^2} + \frac{1}{{(2^N+1)}^2} + \frac{1}{{(2^N+2)}^2} + ... \frac{1}{{(2^{N+1}-1)}^2} < \frac{1}{2^N}

Now if we sum all the LHS and all the RHS then we get S < 1 + 1/2 + 1/3 + ¼ + …. < 2

The only thing that's left is to prove the 'general case' above.... -

Let's write down the 2 N 2^N element:

1 ( 2 N ) 2 = 1 2 2 N \frac{1}{{(2^N)}^2} = \frac{1}{2^{2N}}

1 ( 2 N + 1 ) 2 < 1 2 2 N \frac{1}{{(2^N+1)}^2} < \frac{1}{2^{2N}}

1 ( 2 N + 2 ) 2 < 1 2 2 N \frac{1}{{(2^N+2)}^2} < \frac{1}{2^{2N}}

.....

1 ( 2 N + 1 − 1 ) 2 < 1 2 2 N \frac{1}{{(2^{N+1}-1)}^2} < \frac{1}{2^{2N}}

If we add them up then we get the 'general case'

1 ( 2 N ) 2 + 1 ( 2 N + 1 ) 2 + 1 ( 2 N + 2 ) 2 + . . . 1 ( 2 N + 1 − 1 ) 2 < 1 2 2 N + 1 2 2 N + . . . + 1 2 2 N = 1 2 N \frac{1}{{(2^N)}^2} + \frac{1}{{(2^N+1)}^2} + \frac{1}{{(2^N+2)}^2} + ... \frac{1}{{(2^{N+1}-1)}^2} < \frac{1}{2^{2N}} + \frac{1}{2^{2N}} + ... + \frac{1}{2^{2N}} = \frac{1}{2^N}

4 Helpful 0 Interesting 0 Brilliant 0 Confused

Can we find it's exact value?

Mihul Yadav - 4 years, 3 months ago

Log in to reply

pi^2/6. See basel theorem .

Aviel Livay - 4 years, 3 months ago

@Aviel Livay I couldn't understand 'FINITE' , isn't the series INFINITE??

Ankit Kumar Jain - 4 years, 3 months ago

Log in to reply

It's finite :) if you add more and more members of this series you are gonna end up with a number and we know that this number is smaller than 2.

Aviel Livay - 4 years, 3 months ago

Log in to reply

Okay, I know that the number is less than 2 , but how is it finite? Isn't it that we can reach upto infinite terms ?

Ankit Kumar Jain - 4 years, 3 months ago

Log in to reply

@Ankit Kumar Jain – You are asked about the value of the sum, not about the number of terms.

The value of the sum is finite. The number of terms is infinite.

Calvin Lin Staff - 4 years, 3 months ago

Log in to reply

@Calvin Lin – I got it now , Thanks!

Ankit Kumar Jain - 4 years, 3 months ago

The series is an Infinite one, but the solution for its VALUE for an infinite number of factors n & n--- >oo, is Finite, which means it Converges to a constant value.

Conrad Winkelman - 1 year, 10 months ago

Ohhh sorry, I did not notice that the question was already answered!

Conrad Winkelman - 1 year, 10 months ago
Ankit Kumar Jain
Feb 17, 2017

Consider the sum :

S = 1 1 × 2 + 1 2 × 3 + 1 3 × 4 + ⋅ ⋅ ⋅ S = \frac{1}{1\times 2} + \frac{1}{2\times 3} + \frac{1}{3\times 4} + \cdot \cdot \cdot .

S = 1 − 1 2 + 1 2 − 1 3 + 1 3 − 1 4 + 1 4 ⋅ ⋅ ⋅ S = 1- \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + \frac{1}{4} \cdot \cdot \cdot

⇒ S < 1 \Rightarrow S < 1 .

1 2 2 < 1 1 × 2 \frac{1}{2^2} < \frac{1}{1\times 2}

1 3 2 < 1 2 × 3 \frac{1}{3^2} < \frac{1}{2\times 3}

1 4 2 < 1 3 × 4 \frac{1}{4^2} < \frac{1}{3\times 4} and so on.

⇒ 1 > S > 1 2 2 + 1 3 2 + 1 4 2 + ⋅ ⋅ ⋅ \Rightarrow 1 > S > \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdot \cdot \cdot

⇒ 2 > S + 1 > 1 1 2 + 1 2 2 + 1 3 2 + 1 4 2 + ⋅ ⋅ ⋅ \Rightarrow 2 > {S + 1} > \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdot \cdot \cdot

3 Helpful 0 Interesting 0 Brilliant 0 Confused

I like your explaination

Rodo Anh - 3 years, 7 months ago

Log in to reply

Thanks.!! :)

Ankit Kumar Jain - 3 years, 6 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...