Rectangles and squares
A rectangle of a variable size is chosen at random from the 8 × 5 grid.
What is the probability the chosen rectangle has a vertex at point A ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
21 solutions
This is the most rustic, comprehensive explanation one could fathom. Excellent work, mate.
Sorry, I didn't understand why you divided by four the first time and not the second time
Log in to reply
The first time we can draw each one of the rectangles in 4 different ways, by placing the first point at any of the four corners and the second at the opposite corner. This means we are counting each rectangle 4 times, and have to divide by 4. However, for the second time, we start drawing each rectangle in the same place (at A), and so we are not counting rectangles multiple times.
Beautiful solution. I understood it perfectly
I was considering also oblique rectangles :D
I do not understand why we're not dividing by 4 the second time. I get that we don't have to choose A, just the second, opposite corner, but even then, marking the second (opposite) corner will automatically generate two more corners ( fixed w.r.t. A and our chosen corner) and we can still draw a rectangle from all 4 points (and still have A as a corner). It just appears to me that we are deliberately choosing to not draw rectangles from other points (But still arrive at the right conclusion which is sort of confusing).
Log in to reply
We are deliberately choosing to draw each rectangle only from A. In the first case we divide by 4 because we counted each rectangle 4 times, but when we draw each rectangle from A each rectangle is only being counted once. The second point is the only thing that varies, and each location of the second point produces a unique rectangle when the first point is fixed at A.
where do you take into account oblique rectangles?, like the ones with length sqrt(2)x2sqrt(2)
Log in to reply
If it were a grid of vertices, I would have to consider diagonal rectangles as well. However, the question simply states "A rectangle is chosen from the 8x5 grid." This suggests that new lines aren't being created, and so there would be no oblique rectangles.
Consider making a rectangle first and then placing point A. Since the position of A has nothing to do with the rectangle, that is valid. Now the ending of the solution is obvious: there are 54 possible places for A out of which 4 fit the conditions, so the answer is 5 4 4 = 2 7 2 .
I'm not sure i follow your reasoning... Can you show a diagram of the "54 possible places for A"?
Log in to reply
There are 6 x 9 place to put A point,you need to look grid as points,not lines.
Log in to reply
Oh, so all 54 points are equiprobable? Mkay, that simplifies things. :-)
Excellent solution!!!
How do 4 points satisfy the conditions? Because there are 4 points in any given rectangle?
Log in to reply
'call a point A, then pick a rectangle R at random; what's the probability a corner of R is A?'
is equivalent to
'call a rectangle R, then pick a point at random; what's the probability the point A is a corner of R?'
let's say that if the A we pick happens to be a corner of R it's a success; what's the chance of success? there are 4 success states (the four corners) and a total of 54 points to choose from, so there's a 4/54 chance of success.
Log in to reply
But... are those really equivalent? How would you even show that? Also, in the 1st scenario, point A was known. But in the 2nd, do we know where R is? Do we call the point picked at random "A" or is "A" the point from the problem?
Log in to reply
@C . – Actually,in every condition this method works.The logic is true.
@C . – yeah, I'm not saying the equivalence is obvious, I just reworded the solution a Chris had a doubt about to try to clear that specific doubt.
To try answer your doubt, though, imagine drawing a rectangle, calling it R, and then putting a grid over it with 6x9 points, 4 of which are the corners of R. None of these points is called A: we call A whatever point we happen to fall on (just as we could have called R whatever rectangle we obtained by chance in the original problem).
In this case the problem fixed the point A, and asked: considering the set with all point rectangle pairs (PointsxRectangles), some pairs (A, ?) have ? such that ? has a corner in A (good A pairs), some don't. What's the ratio bewteen the good pairs with A and the total pairs with A (ratioA)?
But, if a good pair, in general, is a point-rectangle pair where the point is a corner of the rectangle, that ratio is the same as the one between good pairs an total pairs (Overall ratio, Oratio), as i'll show. Note that ratioA=ratioB, so the sum of all ratios is n(ratioA), for n points. but the sum of all ratios is also (A,RwithA)/(A, any R)+ (B, RwithB)/(B, any R)+ ..., so let' calculate it another way.
the denominators are the same number, which is (total pairs)/n. So, the numerator of the sum is the sum of the numerators, which is total number of good pairs.
So, the sum is (good pairs)/((pairs)/n)=n(good pairs)/pairs= n*Oratio.
that gives us ratioA=Oratio, and you can imagine the same argument can be made for the rectangles: ratioR=Oratio.
Therefore ratioA=ratioR, therefore fixing one or the other doesn't change the result.
I'm sure there's a simple explanation, or an explanation on the same idea simpler to read, but that's the best I could manage.
Log in to reply
@Samuele Zardo – Almost convincing, but you assume that ratioA = ratioB... Which, again, isn't necessarily obvious. :-(
But thanks for spending the time trying to clarify these things. :-bd
"Specify a particular letter of the alphabet, then pick a random surname from the phone book; what's the probability that the surname begins with the chosen letter?" is not equivalent to "Select a name from the phone book, then pick a random letter of the alphabet; what's the probability that letter begins the surname"
The first probability will vary depend on the letter chosen. If you specify 'B' the probability will be greater than if you specify 'X'. The second probability is always 1/26. (For example, select the name 'Smith' and a random letter has a 1/26 chance of being S.)
You are assuming that the position of A is irrelevant to the answer. Why? It may be that if the diagram above placed A in a corner, then the probability of a random rectangle having a vertex at A would be different from the probability when A is in the more central position shown. (Even if the position of A is indeed irrelevant, this is not immediately obvious and needs to be proved.)
I got it! First, we can prove that whatever A located in, the probability is the same. Thus the problem is equivalent to "point A is random as well as rectangle R is random". Thus the problem is equivalent to "rectangle R is fixed and point A is random". How to prove this? We can see Joseph Newton's method, the most upvoted solution.
It supposes that the probability we are looking for is the same for any position of the point A. You would need to prove that as well!
I think you need to clarify that we consider rectangles with sides on a grid lines. It is possible to create rectangles with sides having neither horizontal nor vertical direction.
Log in to reply
Thanks for comment,I get the point but this might be too hard to solve and the first idea that we get when we looked to question is "I need to calculate horizantal and vertical combinations."But thanks for the idea,interesting perspective...
Since you said rectangles only, I calculated as you but excluded the squares, 540 -100 = 440 possible rectangles. Then out of the ones with corner point also excluded the squares. 40 - 10 = 30. So my answer is 3/44.
Log in to reply
I understand,when I contributed the question;the explanation was different.In my first explanation,I mentioned about it.Nearly 3 weeks later,I think Brilliant Staff controlled the English for “Problem Of The Week”and they corrected the vocabulary mistakes.So I think,square is also a rectangle.
If I recall, a square has all properties of a rectangle so I guess it qualifies ;)
We note that any pair of vertical lines and any pair of horizontal lines in the grid form a rectangle. Since it is a 8 × 5 grid, there are 9 vertical lines and 6 horizontal lines, and the total number of possible rectangles can be formed is N = ( 2 9 ) ( 2 6 ) = 5 4 0 .
By fixing A , we fix a vertical line and horizontal line through A for the two sides the rectangle, we can only select the remaining vertical line from the remaining 8 vertical lines and the remaining horizontal lines from the remaining 5 horizontal lines. The the number of rectangles with a vertex at A is N A = ( 1 8 ) ( 1 5 ) = 4 0 .
Therefore, the probability of rectangles with a vertex at A is p = N N A = 5 4 0 4 0 = 2 7 2 .
There are 9x6 = 54 potential vertices to create a rectangle in this box. A rectangle has 4 vertices (a square is a type of rectangle). So the probability that A is one of those is 4/54 = 2/27
This is by far the simplest and best solution. I really liked the most upvoted one, and liked it best, until I saw this.
Generalization :
For n × m grid the probability is: ( n + 1 ) ( m + 1 ) 4
A rectangle is defined by two pairs of parallel grid lines. There are ( 2 n + 1 ) ⋅ ( 2 m + 1 ) of them in total.
A point A is defined as an intersection of two perpendicular lines. It follows that the number of rectangles with vertex A is equal to ( 1 n + 1 − 1 ) ⋅ ( 1 m + 1 − 1 ) = n ⋅ m .
The probability is the ratio of these two quantities: ( 2 n + 1 ) ⋅ ( 2 m + 1 ) n ⋅ m = 2 ( n + 1 ) n ⋅ 2 ( m + 1 ) m n ⋅ m = ( n + 1 ) ( m + 1 ) 4
For a vertex to land on A , both a horizontal line and a vertical line must land on A .
The chance of the first chosen vertical line landing on A is 9 1 . For the remaining 9 8 times where the line misses, there is now a 8 1 chance of the second vertical line landing on A . This gives us a 9 1 + 8 1 × 9 8 = 9 2 chance of one of the vertical lines being correct.
Similarly, the chance of a horizontal line landing on A is 6 1 + 5 1 × 6 5 = 6 2 .
The chance of both of these conditions being true is therefore 9 2 × 6 2 = 2 7 2 .
A random rectangle is selected by apppointing two different horizontal lines, and two different vertical lines. The probability that A is on one of the chosen horizontal lines is 6 2 , the probability that A is on one of the chosen vertical lines is 9 2 . The probability that A is on a vertex corresponds to the probability that both above conditions are met, and (since the choices of horizontal and vertical lines are independent) this is just their product: 6 2 × 9 2 = 2 7 2 .
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
|
Output:
40 / 540
, which we reduce to
2
/
2
7
.
And what did this program print?
Log in to reply
It printed
40 / 540
, which of course reduces to
2
/
2
7
.
(I typed that in my solution, but for some reason Brilliant does not display text after a
code block
in the solutions.)
Log in to reply
Oh, i see it now. It's still there, but hidden behind the code! You can see it by using the "expand" button in the top-right of the code. I guess a dirty workaround is to add more line breaks between the code and the text following it?
Arjen -- Is that written in C ?
Log in to reply
Yes, this is traditional C.
Log in to reply
Thanks. I thought that it looks familiar - but wasn't sure. Have you dabbled with C# ?
Log in to reply
@Monty McGee – No, I have worked with C++ and Java, but not with C#.
There are 6 horizontal lines where two sides of the rectangle may lie, so 1 / 3 may have a vertex on A. Of these 2 / 9 verticals will have a vertex on A. So the probability will be 1 / 3 ∗ 2 / 9 = 2 / 2 7 .
This is the solution I used. There is no need to count the ways to choose the lines. If we assume that the random distribution is such that each horizontal line is chosen as frequently as any other horizontal line, all we need to know is the relative density of chosen lines, 2/6. Same applies to vertical lines, 2/9.
It doesn't matter the shape or layout of the 4 selected vertices. There are 54 (9 * 6) potential vertex points, and there are always 4 chosen vertices. 4/54 = 2/27.
This is even simpler than the solution I used. If a rectangle is defined by its vertices, and we have a random distribution where each such rectangle is equally likely, then each point in the grid is equally likely to be a vertex.
Of course there are many ways to skim the cow. For example, we could have a random distribution where each possible width and height of the rectangle were equally likely. This would favor the points near the extremities of the grid. The choice of the random variables does matter.
Here's how i found the answer without actually solving it. I counted the number of possibilities in the sample space (9x6=54) and found the denominator from given options which is a multiple of 54.
I just made a guess, I only know that the total number of rectangles in the figure is 540... So, we need to find the probability of a rectangle having vertex A ,
∴ , it is obvious that the denominator should be 5 4 0 .. and in the options the only number which is a factor of 540 is 27!
Hence, the answer is 2 7 2 !
The total number of rectangles is ( 2 9 ) × ( 2 6 ) .
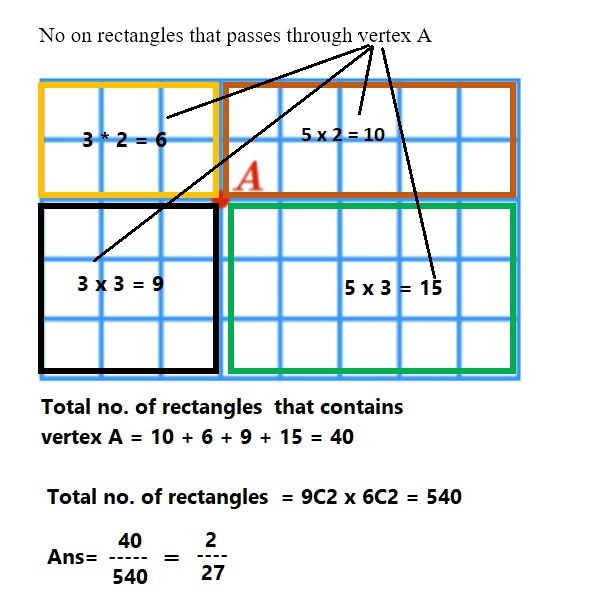
The number of rectangles with vertex A can be divided up into 4 sections.
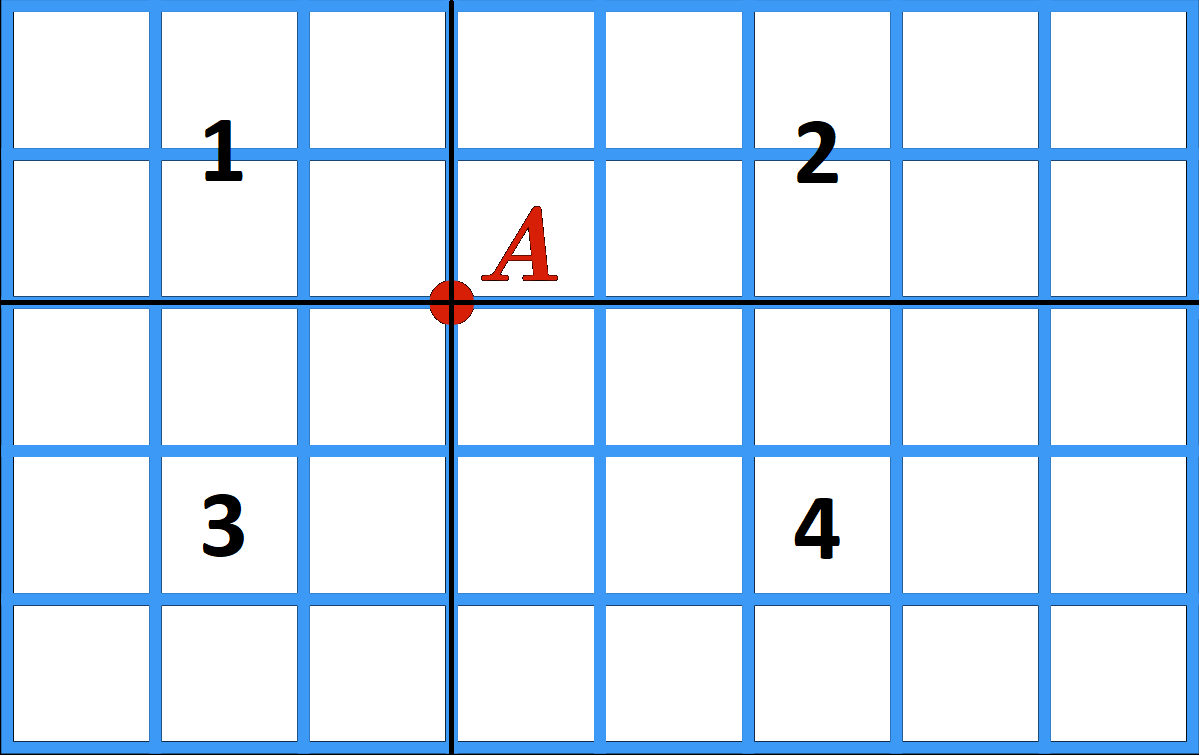
For each section we only have to count the different possible opposite corners:
Section 1: 3 × 2 = 6 . Section 2: 5 × 2 = 1 0 . Section 3: 3 × 3 = 9 . Section 3: 5 × 3 = 1 5 .
Adding those up and dividing them by the to total number of rectangles gives up the answer:
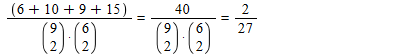
There are ( 2 6 ) × ( 2 9 ) = 4 5 × 6 × 8 × 9 = 5 4 0 sub-rectangles in the given 8 × 5 grid of which 4 0 sub-rectangles have A as a vertex. As such, the desired probability is 5 4 0 4 0 = 2 7 2 .
For you to be able to draw a rectangle from a grid, you need 2 parallel vertical and horizontal lines. So to get the total number of rectangles you can draw in an 8x5 grid, you can choose 2 from 9 vertical lines and 2 from 6 horizontal lines. Thus, ( 2 9 ) x ( 2 6 ) = 36 x 15 = 540.
You can separate the 8x5 grids into four quandrants setting point A as the origin. Here you will be able to create 4 smaller grids (3x2, 5x2, 3x3 and 5x3). To make sure that the vertex of the rectangle falls on point A, you can set the vertical and horizontal line already passing at point A. This means that for the 3x2 grid, you only get to choose 1 from the 3 remaining vertical lines and 1 from the 2 remaining vertical lines. Thus, ( 1 3 ) x ( 1 2 ) = 3 x 2 = 6. Applying to the other grids, you obtain 10, 9 and 15 respectively.
Thus, the probability the rectangle has a vertex at point A is 5 4 0 6 + 1 0 + 9 + 1 5 = 2 7 2 .
The probability of random rectangle is touching vertex A by any of its vertices is 1/(6x9) = 1/54. Since every rectangle has 4 vertices, the probability is 4/54 => 2/27.
The total number of rectangles with the top left being the first square on the grid is 8 × 5 . The total number of rectangles with the top left being the second square on the grid is 7 × 5 . This pattern continues, so the total number of rectangles with the top left being on the first row of the grid is 8 × 5 + 7 × 5 + 6 × 5 + . . . 1 × 5 = 5 × ( 8 + 7 + 6 + . . . + 1 ) .
The same logic can be applied to the second row, but the column length is four instead of five, so the total number of rectangles with the top left being on the second row of the grid is 4 × ( 8 + 7 + 6 + . . . + 1 ) . The pattern continues, so the total number of rectangles is 5 × ( 8 + 7 + 6 + . . . + 1 ) + 4 × ( 8 + 7 + 6 + . . . + 1 ) + 3 × ( 8 + 7 + 6 + . . . + 1 ) + . . . + 1 × ( 8 + 7 + 6 + . . . + 1 ) = ( 5 + 4 + . . . + 1 ) ( 8 + 7 + 6 + . . + 1 ) = ( 2 5 × 6 × 2 8 × 9 = 1 5 × 3 6 .
If any square is chosen on the grid, a unique rectangle can be created with A and that square being opposite corners of the rectangle. Therefore the total number of rectangles with point A as a vertex is 8 × 5 = 4 0 .
The total probability, therefore, is 1 5 × 3 6 4 0 = 2 7 2 .

Every rectangle on the grid can be drawn by choosing two points on different vertical and horizontal lines and making them the corners of a rectangular box, for example: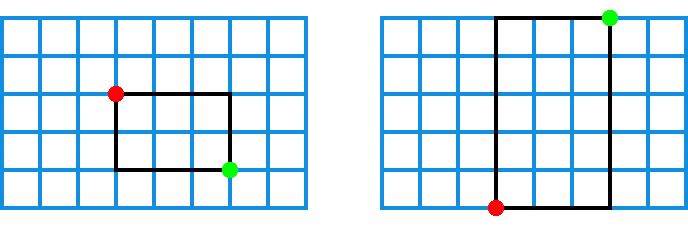 Using this, we can calculate the total number of rectangles. To pick the first point, there are 6 horizontal lines and 9 vertical lines, so the total number of places to put the first point is
6
×
9
. For the second point, we can't put it on the same row or column, so there are only
5
×
8
places to put it. After multiplying these together, we need to divide by 4, as each rectangle can be drawn from any of its 4 corners, and so the total number of rectangles is
4
6
×
9
×
5
×
8
=
5
4
0
.
Using this, we can calculate the total number of rectangles. To pick the first point, there are 6 horizontal lines and 9 vertical lines, so the total number of places to put the first point is
6
×
9
. For the second point, we can't put it on the same row or column, so there are only
5
×
8
places to put it. After multiplying these together, we need to divide by 4, as each rectangle can be drawn from any of its 4 corners, and so the total number of rectangles is
4
6
×
9
×
5
×
8
=
5
4
0
.
Now, to find the number of rectangles with a corner at A, we can just let the first point we draw the rectangle from be A and the second point be on some other vertical and horizontal line, so the total number is 5 × 8 = 4 0 . Note that we don't need to divide by anything, because all the rectangles are being drawn from the same starting corner.
This means the probability of choosing a rectangle with a corner at A is 5 4 0 4 0 = 2 7 2