Rectangle in an hexagon
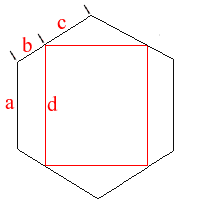 Let a be 2 units. If the corners are touching the midpoints of the sides, i.e. b=c.
Find the area of of the rectangle.
Let a be 2 units. If the corners are touching the midpoints of the sides, i.e. b=c.
Find the area of of the rectangle.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Solution: Let e be the horizontal line joining the midpoints of the adjacent sides of the hexagon. You can get the size of e by using a the cosine rule: - e 2 = 1 2 + 1 2 − 2 × 1 × 1 × c o s ( 1 2 0 ° ) = 3 - e = 3 - Now we need to find d (of the image). Observe that the diagonal of the rectangle is equal to the height of the hexagon. It is equal to twice the apothema, which is equal to the height of a equlateral triangle of side 2. The height is: 2 2 = 1 2 + x 2 t h e r o f o r e : x = 3 - So the diagonal of the rectangle is : 2 3 - Using pithaghoras we now can get the size of d (of the image): - ( 2 x ) 2 = e 2 + d 2 - ( 2 3 ) 2 = 3 2 + d 2 solving we get: d = 9 = 3 . -The area of the rectangle is d × e = 3 3
@Ivan Martinez In the wording of your question, I think that you meant to state that b = c , and not that a = b . I knew what your intent was, but this would make the wording consistent with the diagram. :)
Log in to reply
You are right, Thanks! Any idea of how to change it?
Log in to reply
Just hover the mouse over the row of 3 small, square boxes below the question. You will then get a prompt asking if you wish to edit, etc., your question. Just press "edit", make the required changes and then press "save".
Correction: You have to press the 3 box icon to get the process rolling ..... :)
Assuming that b = c = 1 , we first note that since each of the interior angles of a regular hexagon have a measure of 1 2 0 degrees, and since a ∣ ∣ d , we have that
d = a + 2 b ∗ sin ( 3 0 ) = 2 + 2 ∗ ( 2 1 ) = 3 ,
and that the second dimension of the rectangle is
2 c ∗ cos ( 3 0 ) = 2 ∗ ( 2 3 ) = 3 .
Thus the area of the rectangle is 3 3 .