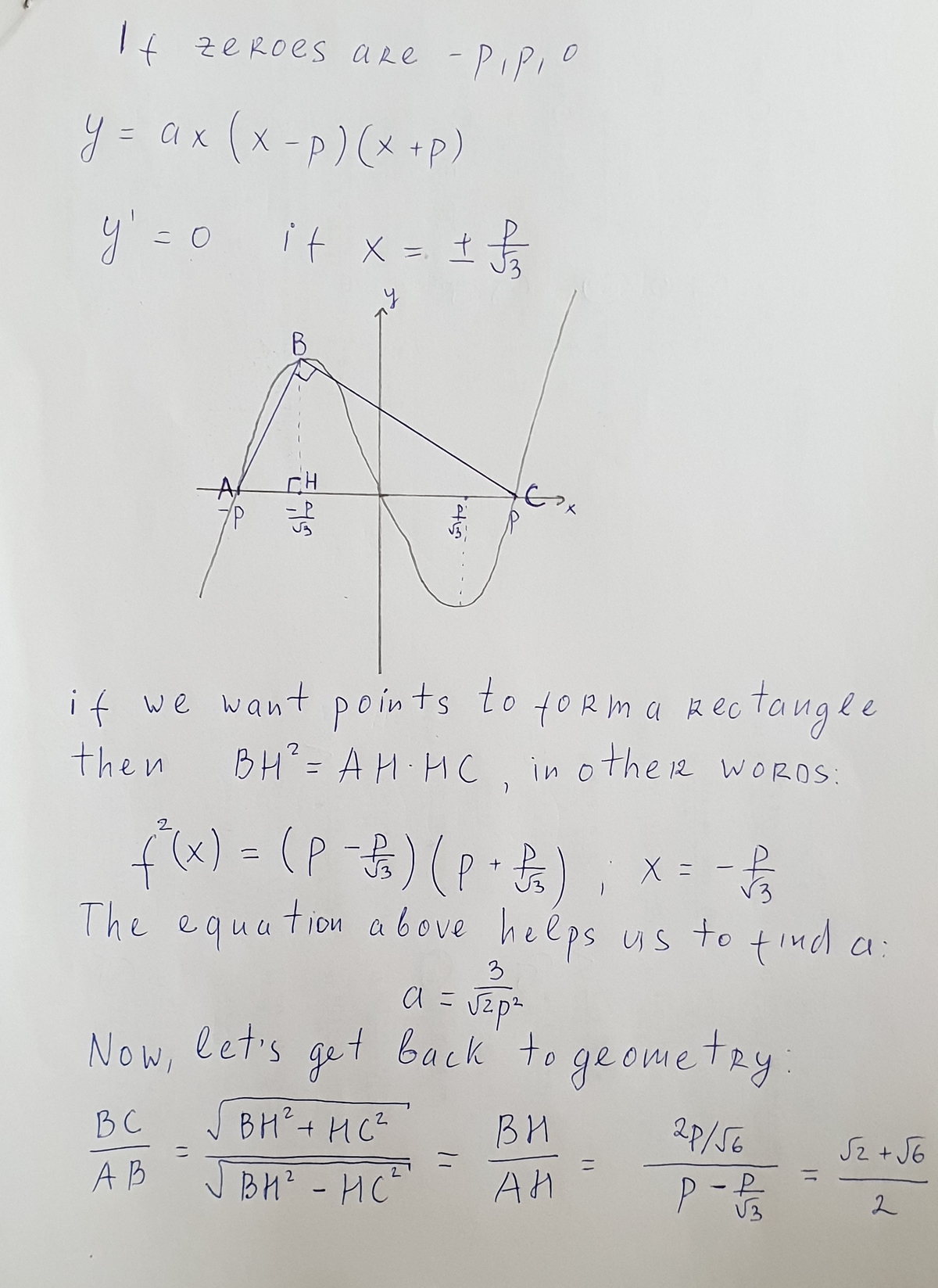Rectangle on a Cubic
If a cubic equation has real zeroes ± p and 0, and its two horizontal tangent points and two non-zero x -intercepts can be joined together to form a rectangle (as pictured), then the ratio of the rectangle’s larger side to its shorter side can be expressed as c a + b , where a , b , and c are square-free integers.
What is a + b + c ?
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Cubic's equation becomes k ( x 3 − p 2 x ) = 0 , where k is a constant.
The four points of the rectangle are the two roots and the points where derivative of the cubic = 0.
3 x 2 − p 2 = 0
x = ± √ 3 p
After putting these x-coordinates in the expression we get the four points as ( p , 0 ) , ( √ 3 p , 3 √ 3 − 2 p 3 k ) , ( − p , 0 ) , ( √ 3 − p , 3 √ 3 2 p 3 k )
Taking the slopes of any two adjacent sides and making their product = -1, we get p = ( 2 k 2 9 ) ¼
The ratio asked for is the value of the slope of the line joining ( − p , 0 ) and ( √ 3 − p , 3 √ 3 2 p 3 k ) , which, after putting in the value of p , comes out to be 2 √ 6 + √ 2
its wrong...... the ratio will come out to be {(3)^(1/2) + 1}/3. and hence the solution to the question is 7. put p=1 and check it for yourself
Log in to reply
p is not a variable here, we cant just set its value to anything, we determine after calculation that its 4 . 5 ¼ . Theres only one value of p for which the situation exists.
Log in to reply
The question seems fairly general though. So maybe putting any value of 'p' should do the trick.
Log in to reply
@Sarthak Baghel – Its not general though, only one cubic exists which can give such a rectangle. You can try putting p=1 and joining all the corresponding points, they would not form a rectangle.
Log in to reply
@Parth Sankhe – the cubic is y=kx(x^2-p^2), different values of k produce different values of p
Log in to reply
@David Dyer – Yeah, but that wouldn't change the value of what is asked
Log in to reply
@Parth Sankhe – true, but it does mean that we can find a value of k such that p=1
Log in to reply
@David Dyer – True, that occurs at k = √ 2 3 . I will make a change to my solution, thanks.
Ratio = slope. That would have saved a lot of work. I actually found the lengths. Using k was also smart. Interesting you never gave the value of p = 4 4 1 8 . I may have to share my hard-way solution.
Log in to reply
Thank you! The suggestion to use k , however, was given to me by @David Dyer in the comments of this solution.
You don't need to go into "the product of 2 gradients is -1". I did that too. Then I noticed that of course the highest semi-diagonal of the rectangle (origin to highest vertex of the rectangle) is of course p because all the semi-diagonals are equal! This makes a nice little Pythag triangle to find p.
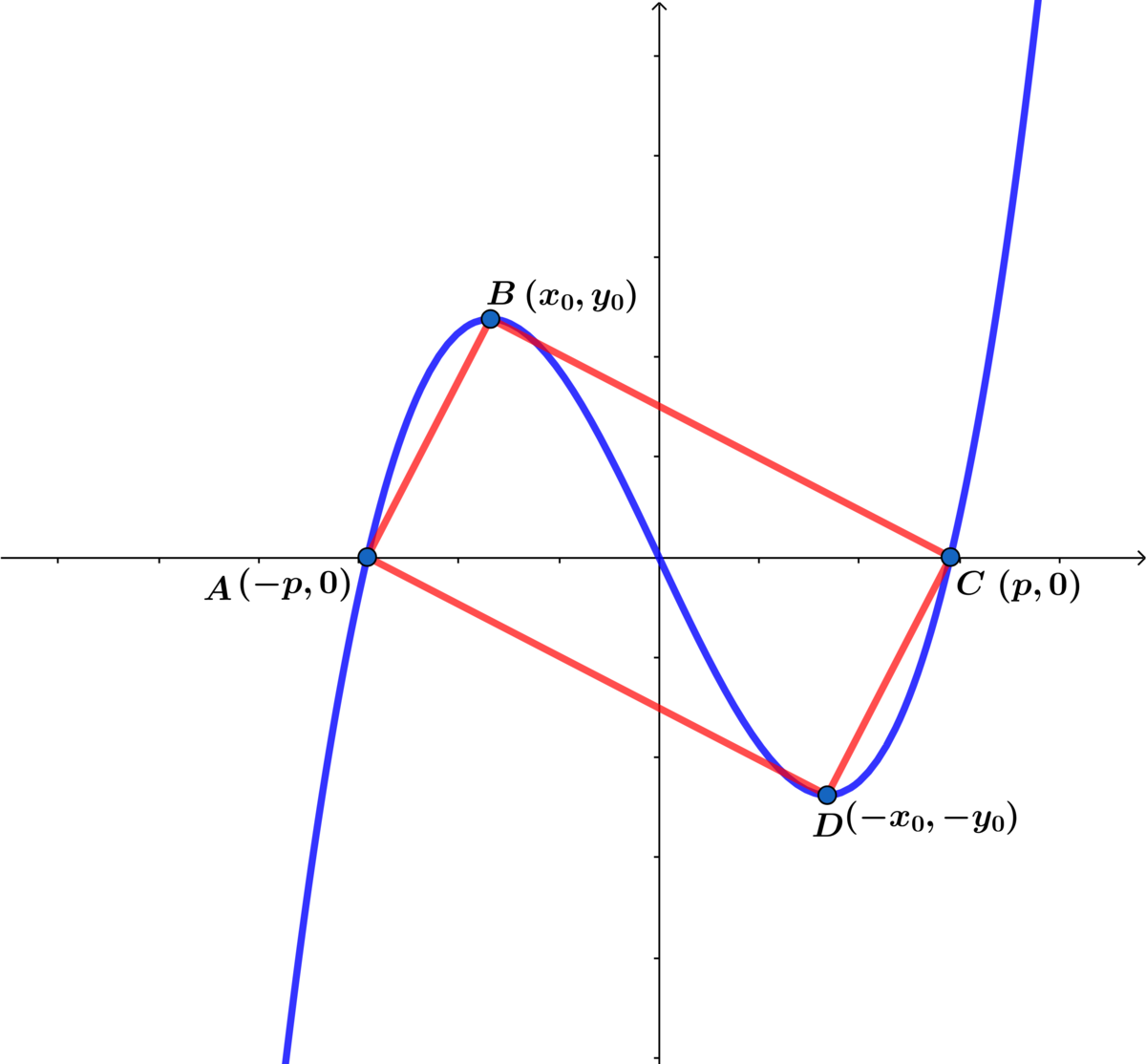
m ( x ) = x ( x − p ) ( x + p ) = x 3 − p 2 x ⟹ d x d m ∣ x = x 0 = 3 x 0 2 − p 2 = 0 ⟹ x 0 = 3 p
B : ( − 3 p , 3 3 2 p 3 ) , D : ( 3 p , − 3 3 2 p 3 )
A C = B D = 2 p = 3 3 2 p 9 + 4 p 4 ⟹ 2 7 = 9 + 4 p 4 ⟹ p 4 = 2 9 ⟹ p = ( 2 9 ) 4 1
⟹ A B = 2 4 1 1 6 − 2 3 and B C = 2 4 1 1 6 + 2 3
⟹ A B B C = 2 3 + 1 = 2 6 + 2 = c a + b ⟹ a + b + c = 1 0 .
You expressed your solution wrong but you got the answer right. It's just a matter of slight changes on your equations to make your solution (not the answer) correct!
Don't get me wrong I am assuming you had the solution in your head already but you were not able to communicate the solution.
Log in to reply
I typed A C B C although I used A B , not A C . Should have typed A B B C .
Changed it to A B B C .
Log in to reply
thanks for changing it but that's not the only one wrong. the 'AC=BD...' is wrong too. One way you could do it is type AC=BD= sqrt(AB^2+BC^2) = ...(and it could simplify to)... 2p = [p/sqrt(3)] * [sqrt(8 + (8/9)*p^2)]
Hnece, p =(9/2)^0.25
-peace & cheers and... Have a Merry Christmas!
Log in to reply
@Gabriel Aliman – A B C D is given as a rectangle and the diagonals of a rectangle are congruent, so A C = B D .
Log in to reply
@Rocco Dalto – that's not what I'm talking about. Yes they are equal, and you are right there. I'm talking about the equation. the equation is right from 'AC = BD = 2p' after that, the equation after it is wrong.
This is the part that I meant was wrong sir.
2p = 2p/[3sqrt(3)] * [sqrt(9 + 4*p^4)]
Log in to reply
@Gabriel Aliman – Oh it's right... SORRY sir ^^.
I had a different (perspective) way of solving it. Then I tested that solution by making sure it could simplify to p = (9/2)^0.25. And, it was right. May I know how you came up with this part of the equation: ' 2p/[3sqrt(3)] * [sqrt(9 + 4*p^4)]'?
Log in to reply
@Gabriel Aliman – Using B : ( − 3 p , 3 3 2 p 3 ) , D : ( 3 p , − 3 3 2 p 3 ) and adding some intermediate steps.
We need to find B D , where A C = 2 p .
A C = B D = 2 p = ( 3 2 p ) 2 + ( 3 3 4 p 3 ) 2 =
3 4 p 2 + 2 7 1 6 p 6 = 2 7 3 6 p 2 + 1 6 p 6 =
3 3 2 p 9 + 4 p 4 ⟹ 2 7 = 9 + 4 p 4 ⟹ p 4 = 2 9 ⟹ p = ( 2 9 ) 4 1
Log in to reply
@Rocco Dalto – Oh okay sir. It turns out I misunderstood that part. -Thank you
@Gabriel Aliman – I rechecked it. My calculations are correct. If not, show me where the error occurred.
The polynomial must be f ( x ) = a ( x ) ( x − p ) ( x + p ) = a x ( x 2 − p 2 ) Its derivative is f'(x)=a(3x^2-p^2), so its extremes are at x 1 = − 3 p and x 2 = 3 p . Without altering the problem, we may assume that a and p both are positive. The maximum value then is
y = f ( x 1 ) = 3 3 2 a p 2
The shape with the zeroes and extrema as its vertices is a parallelogram, in general. Divide up the part of the x-axis between -p and p at x 1 , into lengths
d = p − 3 p and
e = p + 3 p Name the short and long sides of the parallelogram b and c.
We have two known rectangular triangles for which b 2 = d 2 + y 2 c 2 = e 2 + y 2 The condition for our parallelogram to be a rectangle now is
b 2 + c 2 = ( d + e ) 2 which rewrites into y 2 = d e
(Substituting the given expressions for y, d and e into this results in a = p 2 3 , but we won't even need this.)
Now we are ready to calculate the ratio c:b
b 2 c 2 = y 2 + d 2 y 2 + e 2 = 3 2 p 2 + ( 1 − 3 1 3 ) 2 p 2 3 2 p 2 + ( 1 + 3 1 3 ) 2 p 2 = 2 + ( 3 − 1 ) 2 2 + ( 3 + 1 ) 2 = 3 − 3 3 + 3 = 2 + 3 , so b c = 2 + 3
Note: From this point I will use a,b and c as in the problem.
We want this value 2 + 3 in the form c a + b , so we have to solve c 2 a + 2 a b + b = 2 + 3 which splits up into a + b = 2 c 2 4 a b = 3 c 4 From which it is clear that c has to be even. Try the smallest value c = 2 , then a + b = 8 and a b = 1 2 , leading to a = 2 , b = 6 , c = 2 , which indeed is a solution, because it satisfies ( 2 2 + 6 ) 2 = 2 + 3 . The requested answer then is a + b + c = 2 + 6 + 2 = 1 0 .
Taking equation as y=x^3-(p^2)x, first determine,
p^2=3/√2
with condition of perpendicular lines, among three points {-p/√3, 2(p/√3)^3)}, {p,0} and {p/√3, -2(p/√3)^3}.
Now, determine the ratio of side lengths=(1/2)(√6+√2)
Answer=10