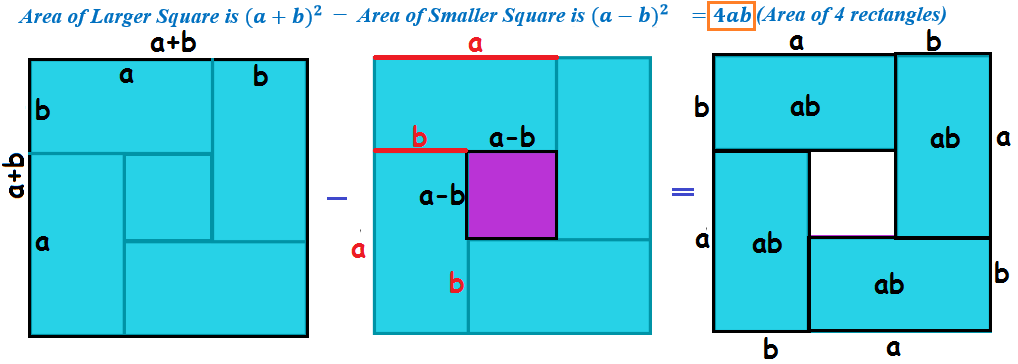
Rectangles and Squares

Algebraically, by difference of squares, $(a + b)^2 - (a - b)^2$ $=$ $((a + b) + (a - b))((a + b) - (a - b))$ $=$ $(2a)(2b)$ $=$ $4ab$ .

Visually, $(a + b)^2$ represents the whole square, $(a - b)^2$ represents the middle purple square, and so its difference is represented by the four $a \times b$ turquoise rectangles with an area of $4ab$ .

Without the aid of the given figure, we can use algebra by simply expanding and simplifying.

$(a+b)^2-(a-b)^2$

Expand the terms inside the parenthesis then collect like terms.

Expanding, we get

$a^2+2ab+b^2-(a^2-2ab+b^2)$

Apply distributive property to remove the parenthesis. We get

$a^2+2ab+b^2-a^2+2ab-b^2$

Collect like terms, we get

$a^2-a^2+b^2-b^2+2ab+2ab=\boxed{4ab}$

looking at $(a + b) ^2 - (a - b) ^2$ the area of the outside square is $(a + b) ^2$ and the area of the purple square is $(a - b) ^2$ . subtracting these two areas leaves us with the area of the four turquoise rectangles which can be expressed as $4ab$ .

$(a + b)^2 - (a - b)^2 =$

$a^2 + 2ab + b^2 - (a^2 - 2ab + b^2) =$

$a^2 - a^2 + b^2 - b^2 +2ab +2ab = \boxed{4ab}$

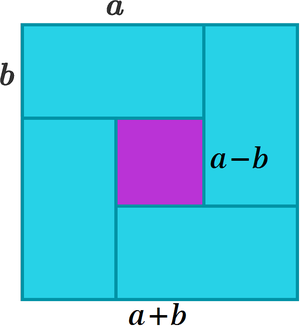
We note that the big square has a side length of $a+b$ and hence an area of $(a+b)^2$ . And the small purple square has a side length of $a-b$ and hence an area of $(a-b)^2$ . Therefore, $(a+b)^2-(a-b)^2 =$ the area of 4 blue turquoise rectangle $\boxed{4ab}$ .

By looking at the picture we can say that for the outer square each side is $a + b$ . So area of outer square is :

$(a + b)^2 = a^2 + b^2 + 2ab$

For, the purple square length of each side = $a - 2b = a - b$ . So, the are of purple square is :

$(a - b)^2 = a^2 + b^2 -2ab$

Now, we have to find $(a + b)^2 - (a - b)^2$

$\implies a^2 + b^2 + 2ab - (a^2 + b^2 - 2ab$

$\implies \cancel{a^2} + \cancel{b^2} + 2ab - \cancel{a^2} - \cancel{b^2} + 2ab$

$\implies 4ab$

So, we are left only with $4ab$ which is the area of the four turquoise rectangles.

Theoretically speaking, by applying the formula of area of rectangle we will get $4ab$ . The four rectangles are equal and length of each rectangle is $a$ and breadth of each rectangle is $b$ .

Area of one rectangle is $ab$ . So the area of 4 rectangles is $4ab$ . This is the result we got above.

Larger square minus the small purple square leaves the four a*b rectangles

We can solve it algebricaly (a+b)^2 -(a-b)^2=???

(a+b)^2=a^2+2ab+b^2

(a-b)^2=a^2-2ab+b^2

(a+b)^2-(a-b)^2=a^2+2ab+b^2-a^2+2ab-b^2

(a+b)^2-(a-b)^2=4ab

At first, we drew a diagram and calculated the area of the whole square which was (a+b)^2 . Then, we figured out the area of the smaller square which was (a-b)^2 . We said that (a+b)^2 - (a-b)^2 must equal the are of the four rectangles on the outside which was 4ab .

However one can recognise the elementary identity (a+b)^2-(a-b)^2=4ab

First $(a+b)^2=a^2+2ab+b^2$ .Next $(a-b)^2=a^2-2ab+b^2$ So $(a+b)^2-(a-b)^2=a^2+2ab+b^2-a^2-2ab+b^2=(a^2-a^2)+(2ab--2ab)+(b^2-b^2)=\color{#3D99F6}\boxed{\large{4ab}}$