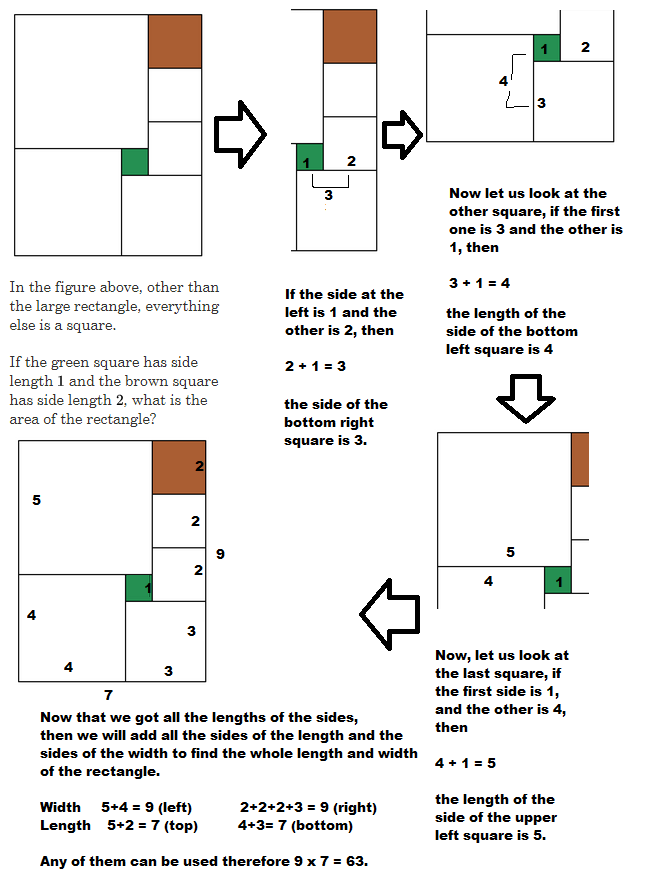
Squares in a Rectangle
 There are 7 smaller squares inside the large rectangle above.
There are 7 smaller squares inside the large rectangle above.
If the green square has side length 1 and the brown square has side length 2, what is the area of the rectangle?
The answer is 63.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
33 solutions
Nice image! The gif makes it so obvious how to calculate the lengths :)
why (4+3)? what about this A = (5 + 4) x ( 2 + 2 +2 + 3) = 81 ?
Log in to reply
Because instead of multiplying length by width you'd be multiplying length by length.
In the bottom right we have a square of size 3 × 3 , in the bottom left a 4 × 4 and in the upper left a 5 × 5 . Thus the area of the rectangle is ( 3 + 4 ) × ( 4 + 5 ) = 6 3 .
Nice way to quickly get the lengths.
The bottom right rectangle is only assumed to be a square. Should've been explained in a clear way, but nice solution.
Log in to reply
I've added that into the question. I forgot to say that they were all squares.
Log in to reply
Brilliant.org thanks you for that :)
They're not all squares. There is a 6x2 rectangle in the upper right hand corner
Log in to reply
@Adam Kaffen – Maybe say something like "In the figure above, the large rectangle contains (or consists of) seven squares." English is my third language... ;)
Extends all the lines and color them......Visualization is much easier

brown square=12 i.e area of brown=(2 2) 12=48 green square=15 i.e area of green=(1 1) 15=15 Therefore, area of the whole rectangle is =48+15=63
Oh, that's a nice way to count them all!
 I hope this explains everything. :)
I hope this explains everything. :)
That's a very detailed image! Thanks!
The shape can be divided into following shape.
There are 12 big squares of area 4.
There are 15 squares of area 1.
Total Area = 12 * 8 + 15 * 1
=48 + 15
= 63
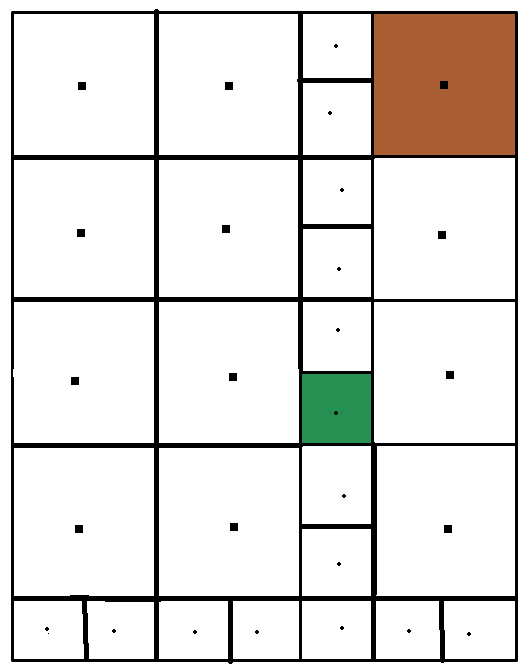
Great image to help explain how to count the lengths
There's one green square (1x1) and two squares congruent with the orange square (2x2). Bottom right square's side is the side of the green and the orange added together and a square so it's (3x3). Same process to get the bottom left square at 4x4 and 5x5 for the top left square. 25+16+9+4+4+4+1=63
Thanks for the explanation!
(2 + 2 + 2 + 3)*(3 + 4) = 63 2 is the base of the upper square, and you have 3 of them. The base of the bottom right square is 2 + 1. You multiply by the base of the bottom right square plus the base of the lower left corner, which is 3 + 1
Nicely done :)
long side = 2*3 =6+3=9
breath side=3+4=7
therefore area= 9*7 = 63
Area= length × breadth
=[(2+2+2+3)×(3+4)]
=9×3
=63 Answer

( 6 + 3 ) × ( 4 + 3 ) = 9 × 7 = 63. Its easy if you DRAW first
It's much easier when you draw it first :)
(1x1)+3(2x2)+(3x3)+(4x4)+(5x5)=63
How did you get those lengths?
Log in to reply
It's said in the problem. One square have a length of 1. A second square have a length of 2. It's juste logic. You see that there is a square that you can combine the square of 1 and the square of 2 to arrive to the length of 3, etc.
2 X 2 = Area of the brown box and the adjacent squares have equal sides so it becomes 4 X 3 (as the three adjacent squares have equal sides). The length of the sides increases from 1<2<3<4<5 which could be interpreted from the diagram so when you add 12 + 9 + 16 + 25 + 1(area of the squares) you get 63
Good approach!
Just looking like a square is not definitive proof that it is a square! So i think picture should be more explained and specified.
How / why?
Log in to reply
He means that the breadth is 7 and the length is 9 so the area is 63
5 X 5 + 2 X 2 + 2 X 2 + 2 X 2 + 3 X 3 + 4 X 4 + 1 X 1 = 63
 1) KC = IJ = IK = 1 + 2 =
3
1) KC = IJ = IK = 1 + 2 =
3
2) DK = EF = FK = FI + IK = 1 + 3 = 4
DC = KC + DK = 3 + 4 = 7 (smaller side of rectangle)
BC = 3 * 2 + JC = 3 * 2 + KC = 3 * 2 + 3 = 9 (larger side of rectangle)
Area of the triangle = DC * BC = 63
given the way, the squares are placed around the 1cm square, we can see easily that: let a be the 2 cm square. and b,c,d the other squared, ordered by size.
then it's obvious that the sidelength of b, the next biggest square , is side length of a plus the 1 cm of the 1 cm square. same goes for b and c: c length=b length+1 d length=c length+1
we find that their lengths are: a=2,b=3,c=4,d=5
then we just need to square all the lengths and add them up, keeping in mind thatt there are 3 2cm squares: 1^2+2^2+2^2+2^2+3^2+4^2+5^2=63
The square at the bottom right has sides of 2 + 1 = 3 . From this we can also deduce that the square at the bottom left has sides of 3 + 1 = 4 .
Thus, the sides of the rectangle are 3 × 2 + 3 = 9 and 3 + 4 = 7 . The area of the rectangle can now easily be calculated as 9 × 7 = 6 3
Area of rectangle = right hand edge x bottom edge. = (2 + 2 + 2+ 3) x (3 + 4) = 63
Area of a rectangle=(length x breadth) So just count the number of boxes and extrapolate to estimate the length of each side and hence the area of the rectange which is (7[vertical] x 9 [horizontal]=63)
Area=(4+3)*(2+2+2+3)=63. Here 7 is the length which is obtained from the length of the sides of the squares......and 9 is the breath.....it is also obtained from the length of the sides of the squares and thus area is obtained.
Vertical distance=(2+2+2+3) and Horizontal distance (3+4). So, (2+2+2+3)×(3+4)=9×7=63
Length is (2+2+2+3) and width is (3+4). So area of rectangle is 9X7=63
4+4+4+1+9+16+25=63
Since the brown square has a side length of 2, and the green square a side length of 1, it follows that the largest square has a side length of 5. Similarly, adding the sides of brown and green gives us a side of 3 for the bottom - right square. Thus, the rectangle's width is 7, and the height 9. The total area therefore being 7 × 9 = 63
L = 2X3+2+1= 9, W = 3+2x2 = 7, Area = LxW = 9x7 = 63
The green has an area of 1, the brown has an area of four. There are three of those size, so 12 as total area. The big one has an area of 25, below it, 16, beside that, 9. Add it all up to 62
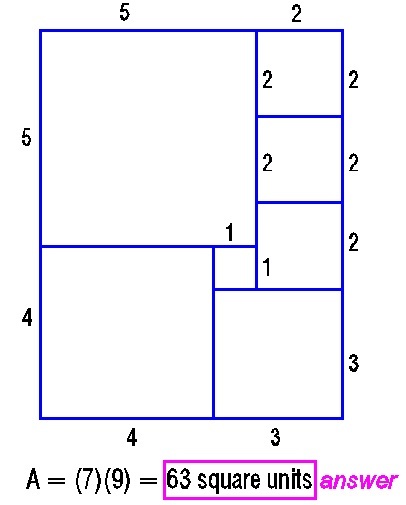


Let A be the total area.