Rectangles in Semicircle
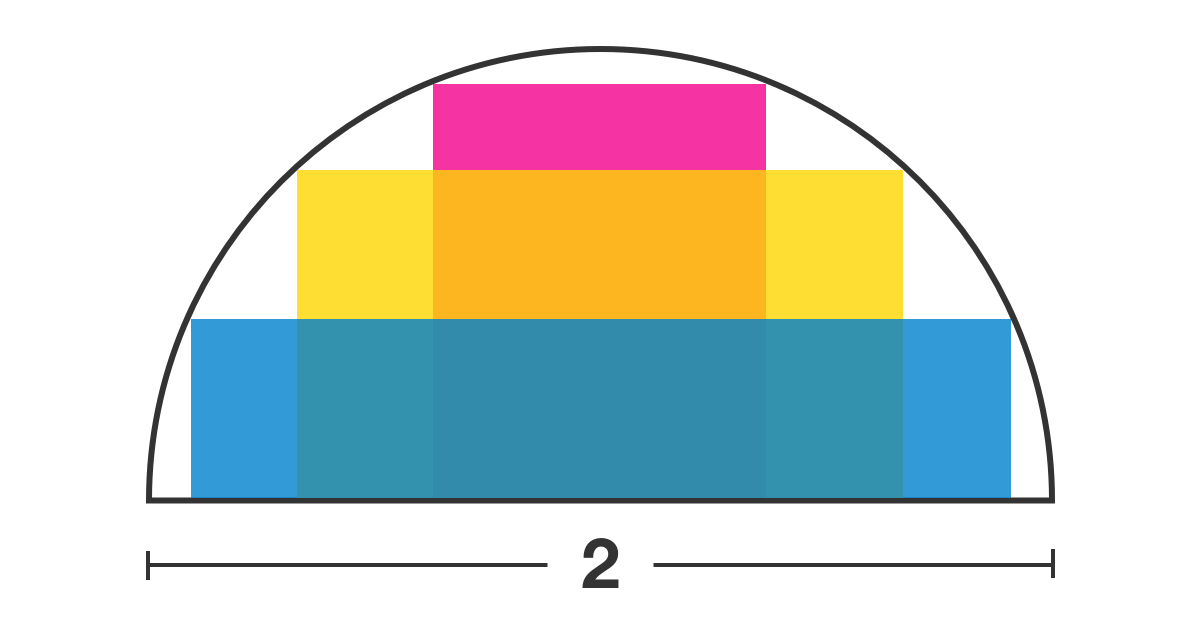
What is the area of the largest rectangle that can be inscribed in a semicircle of radius 1? One side of the rectangle must lie on the diameter.
The answer is 1.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
@Vasilescu Vlad I saw that you posted a solution to this problem, but seem to have deleted it. I've shared my solution which uses some creativity to avoid the calculus.
Pretty good solution . I've deleted my solution because it was unproven .
That's what I did, but in trying to bring in calculus (after reading your comment), I still found a simple approach.
With polar coordinate thinking, we can consider the top-right corner to have coordinates (cos θ , sin θ ) with 0 < θ < 90 ∘ . This makes the area 2sin θ cos θ = sin 2 θ which will obviously be maximised when θ = 45 ∘ , giving an area of 2.
Log in to reply
Oh nice. Can you add that solution?
The calculus approach that I took was to maximize u 1 − u 2 by differentiating with respect to u . It wasn't that bad, mostly just too ugly.
Log in to reply
I've added my alternative solution. Hopefully it is clear enough?
Maximizing $2u \sqrt{1-u}$ is not that ugly in my opinion.
Log in to reply
I do not understand how you are arriving at 2 u 1 − u 2 .
Log in to reply
Let the base of the rectangle be 2 u . What would be the height of the rectangle?
Log in to reply
@Chung Kevin – Sorry but i still don't get it.
Log in to reply
@Rajdeep Ghosh – If the base of the rectangle is 2 u , then the distance from the center of the circle to the lower left corner of the rectangle is u . Since the radius is 1, what would be the height of the rectangle when we apply pythagorean theorem ?
Hence, what is the area of the rectangle by length * height?
With polar coordinate thinking, we can consider the top-right corner to have coordinates:
(cos θ , sin θ ) with 0 < θ < 90.
This makes the area 2sin θ cos θ = sin 2 θ (double angle formula).
As sin 90 ∘ = 1 is a maximum for sine, we can obviously maximise the area when θ = 45 ∘ , giving an area of 2.
Not the way I originally solved it, but a pleasant surprise!
Ah very nice! This expresses Paul's solution without needing polar coordinates :)
Log in to reply
Please see this link text
It is impossible for me to notify you.
Just an important and basic property.
Exactly how I solved it
I couldn't understand it
Log in to reply
I don't see any complications in my solution. Everything seems fine.
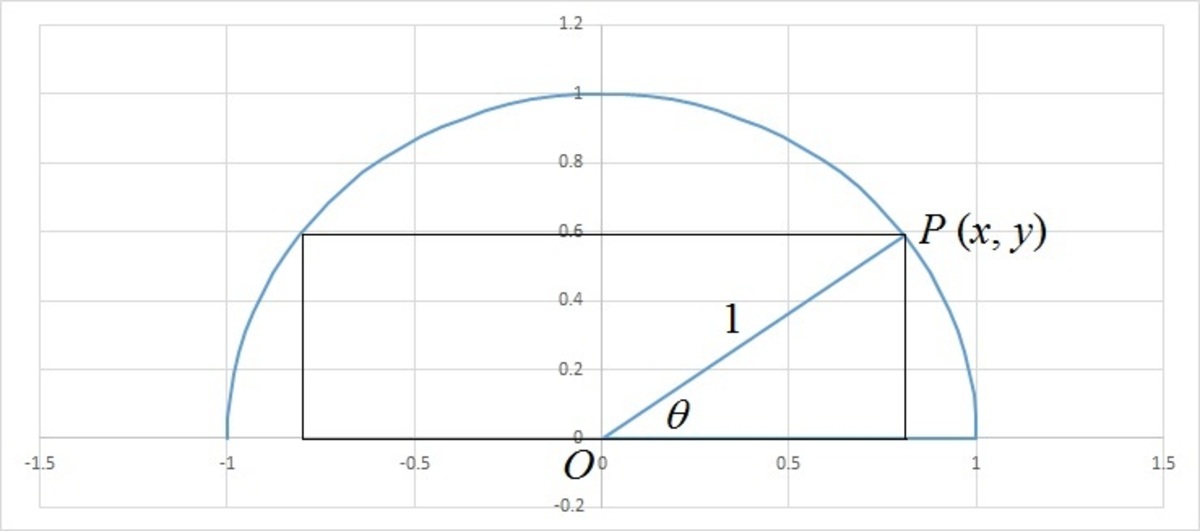
Let the centre of the semicircle be the origin O ( 0 , 0 ) , any point on the arc be P ( x , y ) and the angle O P makes with the x -axis be θ . Then, we have x = cos θ and y = sin θ and the area of the rectangle A = 2 x y = 2 cos θ sin θ = sin 2 θ . Then, A is maximum, when sin 2 θ is maximum that is sin 2 θ = 1 . Therefore, A m a x = 1 .
It is easy! Area = 1. Let's remember that the biggest rectangle in the whole circle is the square. It's Area = (d^2)/2 = 2 and half of that picture is what is shown above,
Try to put a link to an image of this it's hard to see what you mean. Also (even though it's intuitive) why would a square maximize the area in quarter circle?
Let the side on the diameter of the rectangle have length 2 x and the other side have length y . The quantity we want to maximise is 2 x y . By Pythagoras we have:
( 2 2 x ) 2 + y 2 = 1 ⟹ x 2 + y 2 = 1
We then have:
0 ≤ ( x − y ) 2 = x 2 + y 2 − 2 x y = 1 − 2 x y ⟹ 2 x y ≤ 1
This shows that maximum area of the rectangle is 1 which occurs when x = y = 1 .
Oh wow. So many different ways to solve this!
One more "standard" solution: Lagrange multipliers. We want to maximize 2 x y subject to the constraint x 2 + y 2 = 1 ; the relevant system of equations is then
2 y 2 x x 2 + y 2 = 2 λ x = 2 λ y = 1
Substituting the first equation into the second yields x = λ 2 x , so either x = 0 or λ = ± 1 . The first option clearly doesn't give a maximum, and the second option gives x = ± y which now clearly gives the maximum area.
Let the side lengths of the rectangle be a and b , where a is the length of the sides parallel to the diameter.
Notice that 1 = ( 2 1 a ) 2 + b 2 ≥ a b , with equility iff a = 2 and b = 2 1 (since a , b are non-negative).
So, the answer is 1.
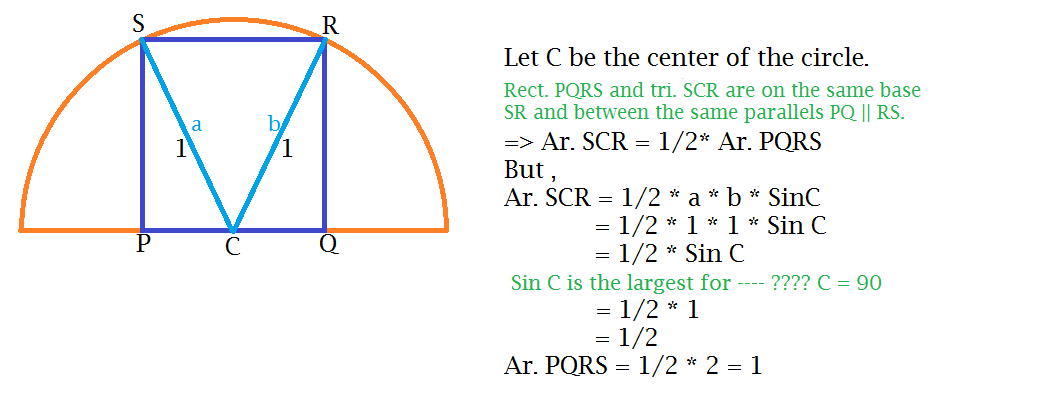
If you ended up doing the calculus to maximize 2 u 1 − u 2 , it is slightly painful / ugly.
However, there is a very simple solution, by doubling the semicircle into a circle, and asking ourselves "What is the area of the largest rectangle that can be inscribed in a circle?". We "know" that it is the square, which has area 2. (Of course, to be certain, we need to come up with a clear explanation.)
Hence, the largest rectangle that can be inscribed in a semicircle, is half of this square, which has area 1.