First, evaluate $a_{0}$ : $a_{1} = 2a_{0} \Rightarrow a_{0} = \frac{3}{2}$

Then, use Z-transform: $a_{n+1} - 2a_{n} + n^2 - n = 0$

$z(\mathbf{A}(z)-a_{0}) - 2\mathbf{A}(z) + \dfrac{z(z+1)}{(z-1)^3} - \dfrac{z}{(z-1)^2} = 0$

$\Rightarrow \mathbf{A}(z) = \dfrac{z(3z^3 -9z^2 + 9z - 7)}{2(z-2)(z-1)^3}$

$\Rightarrow \mathbf{A}(z) = \dfrac{z(3z^3 -9z^2 + 9z - 7)}{2(z-2)(z-1)^3}$

$\Rightarrow \mathbf{A}(z) = \dfrac{2z}{z-1} + \dfrac{z}{(z-1)^2} + \dfrac{z(z+1)}{(z-1)^3} - \dfrac{z}{2(z-2)}$

Working in the inverse of the Z-transform: $\boxed{a_{n} = 2 + n + n^2 - 2^{n-1}}$

Now: $a_{20} = 422-2^{19}$ ; $a_{15} = 242-2^{14}$ ;

$\dfrac{\left\vert a_{20} - a_{15} \right\vert}{18133} = \dfrac{2^{19} - 2^{14} + 180}{18133} = \boxed{\boxed{28}}$

Brute force

Slightly more subtlety

We see that the 3rd and higher differences assume the pattern characteristic of an exponential function. Hence, this is part of the required solution (but not all of it). Accordingly, I remove a convenient exponential component from the terms and recalculate.

And this reveals the remaining quadratic component. We can therefore model the required solution as,

$r{ 2 }^{ n }+s{ n }^{ 2 }+tn+u={ a }_{ n }$

substitute values for $n$ and ${ a }_{ n }$ and solve for the required constants.

r=-1/2, s=1, t=1, u=2

This is correct now.

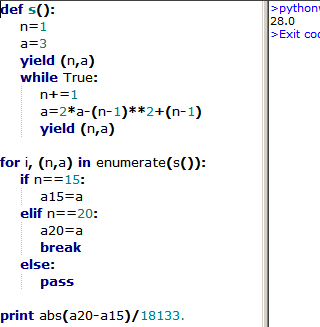
Python

values = {1:3}

def a(n):
    if n not in values:
        m = n-1
        x = 2 * a(m)
        x -= m**2
        x += m

        values[n] = x
        return values[n]
    else:
        return values[n]

print abs(a(20)-a(15))/18133.0

include<stdio.h>

include <stdlib.h>

long int series(int n)

{

if (n==1){return 3;}else{


        long int t=series(n-1);


long int f=2*series(n-1)-((n-1)*(n-1))+(n-1);


return f;


}

}

int main()

{

int i;

scanf("%d",&i);


long int f;f=series(i+5);


long int k;k=series(i);


double p=0;p=(double)f-(double)k;


if(p>0){printf("%f",p/18133);}else


    {printf("%f",-p/18133);}


return 0;

}

NOTE : C language