Recursion Warmup - Hypercube Corners
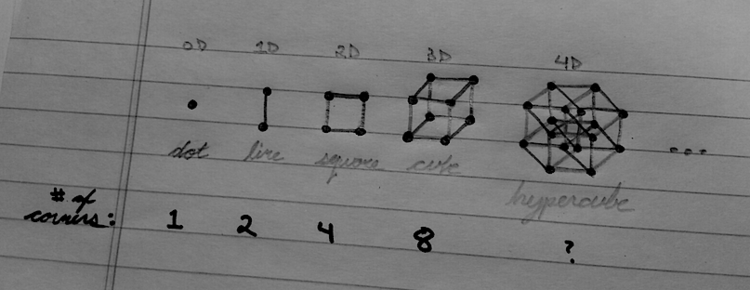 How many corners does a
hypercube
(a 4-dimensional cube) have?
How many corners does a
hypercube
(a 4-dimensional cube) have?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
you sir,are a genius!!
yoo I did by the same way.
Good work!
Is there any way to see the 4d
Log in to reply
Trying to "see" 4D is a misnomer, because we are not trying to visualize 4D, but rather understand the structure. It's not possible to see something that doesn't exist.
Similarly, the fourth dimension is not time [in this case]. Spatial and time dimensions are different, and while they help understanding, they still have fundamental differences.
When you look at a picture of a cube on a sheet of paper, you are looking at a 2D representation of a 3D figure. The relationship is that the picture has the same connecting points and network of the 3D cube, but you take a "snapshot" of it in 2D.
Similarly, what we are doing here is we are taking a 2D representation of a 4D figure, a network of points and lines that would explain how a 4D cube is constructed. We do this by copying the 3D cube and connecting the corresponding vertices.
In summary, rather than trying to "see" something that doesn't exist, try to understand the concepts and relations and representations.
yes, but if you were to see your body in the 4th dimension, you would be like a long snake, with your just-born self on one end and your dead-self on the other.
The number of vertices of a n-dimensional Hypercube is given by 2 n .
Therefore, for a 4-D hypercube, the number of vertices is 16.
Just count:
The answer is 16, 2^4 = 16
It is just 2 cubes right? If u freeze it at the right place u see it is just a cube in a cube?
in dimension (d) the number of verticies are the number on vertices in d-1 multiplied by two
No . That competently wrong
Theres a pattern, everytime a dimension is added the corners need to be doubled to make the figure n-dimension.
Point/dot
=
2
0
=
1
Line/one point to another point
=
2
1
=
2
Square/2-dimensional=2^2=4
Cube/3-dimensional=2^3=8
Hypercube/4-dimensional=2^4=16
FYI To type in Latex, just add \ ( \ ) around the code.
To start a new line, leave 3 empty spaces at the end of the sentence.
I've edited the start of your solution for your reference.
Log in to reply
what do you mean BTW ?
Log in to reply
BTW = By the way
FYI = For your information.
If you are asking what I meant, take a look at the first two lines of your solution, vs the last line.
Log in to reply
@Calvin Lin – aww thank you so much Calvin
@Calvin Lin – May I add you on Facebook ?
2dimentions: 2^2 = 4 corners; 3 dimensions. 2^3 = 8 vertices, 4 dimensions,have 2^4 = 16 vertices or corners.
I had an alternate explanation approach to Mr. Liang While looking at the image I thought of the number of corners in binary 2 0 = 1 , 2 1 = 2 , 2 2 = 4 , 2 3 = 8
2 4 = 1 6
a reference to binary notation: 0b00001 = 2 0 = 01,
0b00010 = 2 1 = 02,
0b00100 = 2 2 = 04,
0b01000 = 2 3 = 08,
0b10000 = 2 4 = 16
Moderator note:
Nice! Could you expand further on this idea of "thinking of the corners in terms of binary"? How does that lead us to 2 4 = 1 6 ?
Nice! Could you expand further on this idea of "thinking of the corners in terms of binary"? How does that lead us to 2 4 = 1 6 ?
FYI To type in Latex, just add \ ( \ ) around the code.
Log in to reply
What was intended was a reference to binary notation 0b00001 = 01 0b00010 = 02 0b00100 = 04 0b01000 = 08 0b10000 = 16
Log in to reply
Great. Could you add that into the solution to make it more explicit? Thanks!
Anyone can just look up a formula for the number of vertices of an n-dimensional hypercube, but it doesn't really explain why this is the case.
When we think about how to define the vertices of any of the figures in the picture, we think to coordinates.
0-dimensions = 1 vertex: ()
1-dimension = 2 vertices: (0) (1)
2-dimensions = 4 vertices: (0,0) (0,1) (1,0) (1,1)
3-dimensions = 8 vertices: (0,0,0) (0,0,1) (0,1,0) (0,1,1) (1,0,0) (1,0,1) (1,1,0) (1,1,1)
By the same pattern, 4-dimensional points would be defined as (a,b,c,d), where a, b, c, and d could be either 0 or 1. Since each of the four variables has two choices, the number of points we have is 2 4 , so our answer is 16.