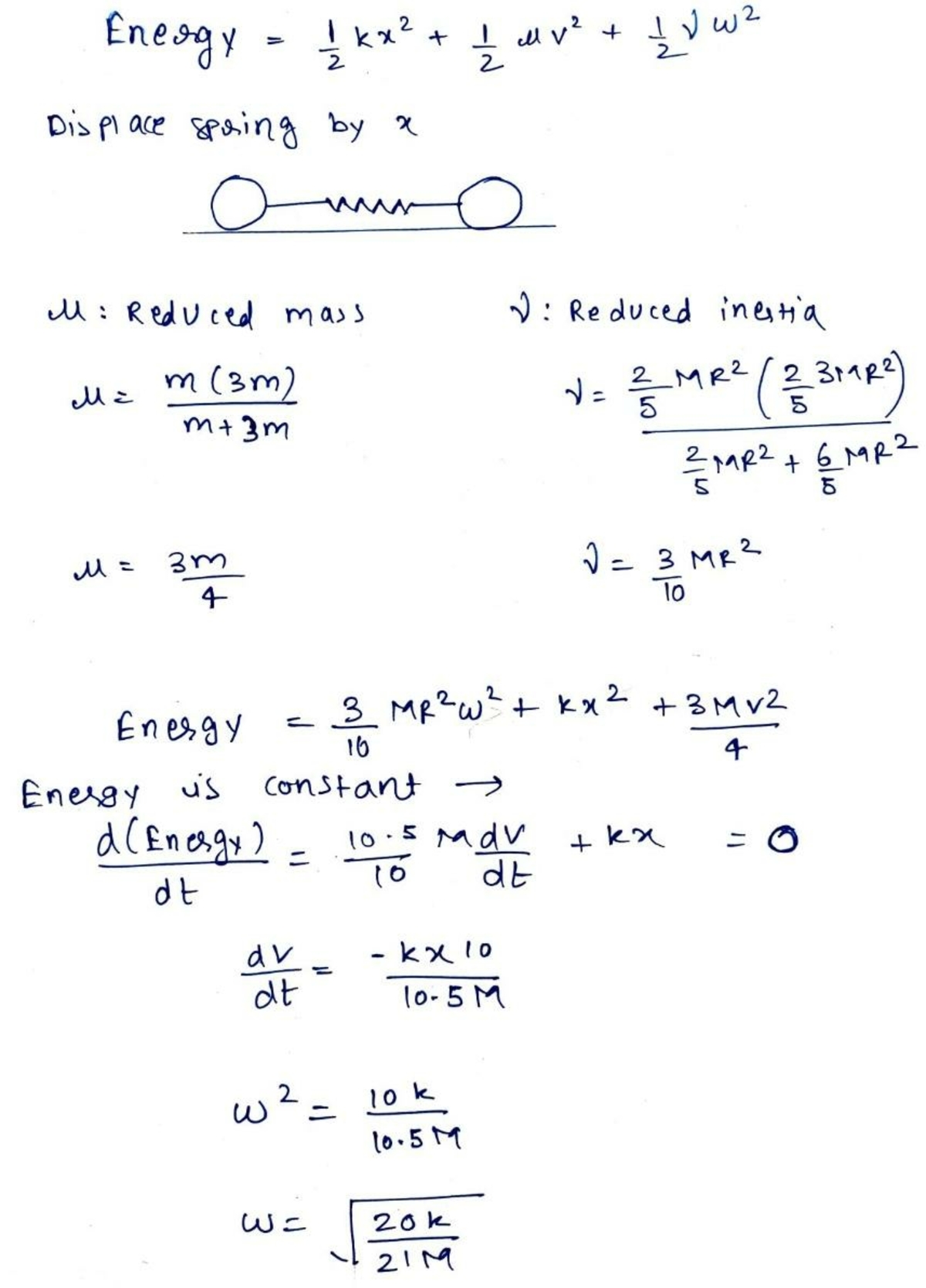
'Reduced' Inertia

I'm actually not familiar with "reduced inertia". I just followed a standard approach to solve.

$m_1 = m \\ m_2 = 3 m$

Accounting for two translational kinetic energy terms, two rotational kinetic energy terms, and the spring potential energy, we have the following Lagrangian.

$L = \frac{7}{10} m_1 \dot{x}_1^2 + \frac{7}{10} m_2 \dot{x}_2^2 - \frac{1}{2} k (x_2 - x_1 - \ell_0)^2$

Evaluating the Euler Lagrange equations results in:

$\frac{7}{5} m_1 \ddot{x}_1 = k(x_2 - x_1 - \ell_0) \\ \frac{7}{5} m_2 \ddot{x}_2 = -k(x_2 - x_1 - \ell_0)$

Substituting for the masses:

$\frac{7}{5} m \ddot{x}_1 = k(x_2 - x_1 - \ell_0) \\ \frac{21}{5} m \ddot{x}_2 = -k(x_2 - x_1 - \ell_0)$

Let $D = x_2 - x_1$ . I want to write a differential equation in $D$ , so multiply the first equation by $3$ .

$\frac{21}{5} m \ddot{x}_1 = 3k(x_2 - x_1 - \ell_0) \\ \frac{21}{5} m \ddot{x}_2 = -k(x_2 - x_1 - \ell_0)$

Now combine:

$\frac{21}{5} m (\ddot{x}_2 - \ddot{x}_1) = -4k(x_2 - x_1 - \ell_0) \\ \frac{21}{5} m \ddot{D} = -4k(D - \ell_0)$

The oscillation comes from the homogeneous equation:

$\frac{21}{5} m \ddot{D} = -4k D \\ \ddot{D} = - \frac{20 k}{21 m} D$

The angular frequency is therefore:

$\omega = \sqrt{\frac{20 k}{21 m}}$

Nice problem. Thanks for inspiration